- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Объём пирамиды (11 класс)
Содержание
- 1. Презентация по математике на тему Объём пирамиды (11 класс)
- 2. Проверка домашнего задания:
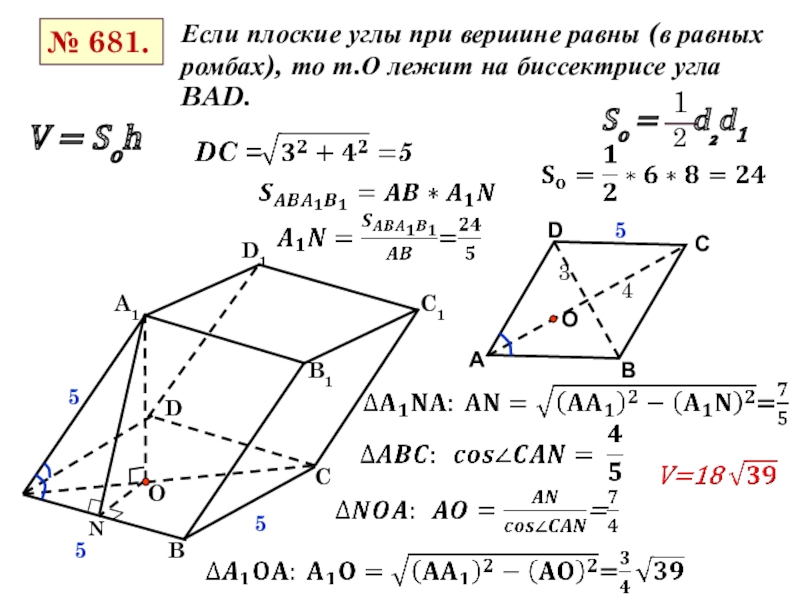
- 3. D1Если плоские углы при вершине равны (в
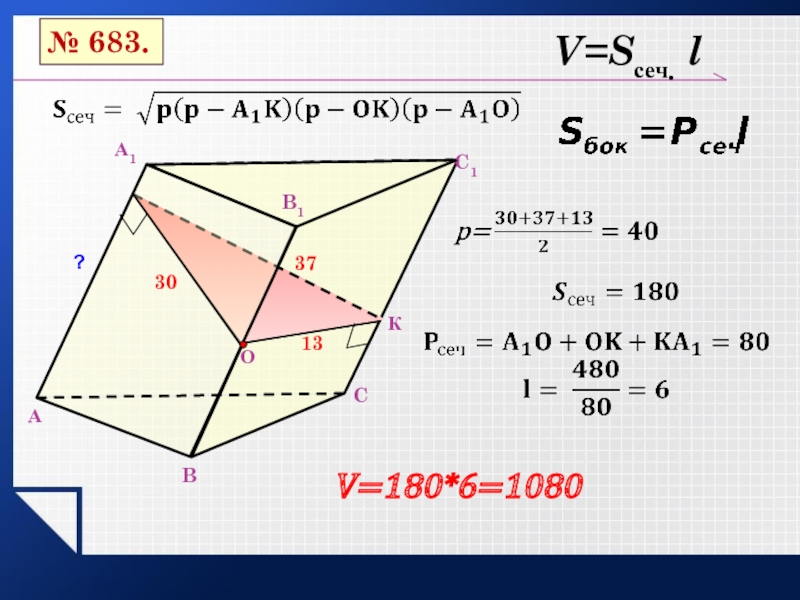
- 4. АB ?C1B1А1 C 3013№ 683.37V=Sсеч. l V=180*6=1080
- 5. Устная работа:
- 6. Слайд 6
- 7. 5
- 8. hV = Soснh
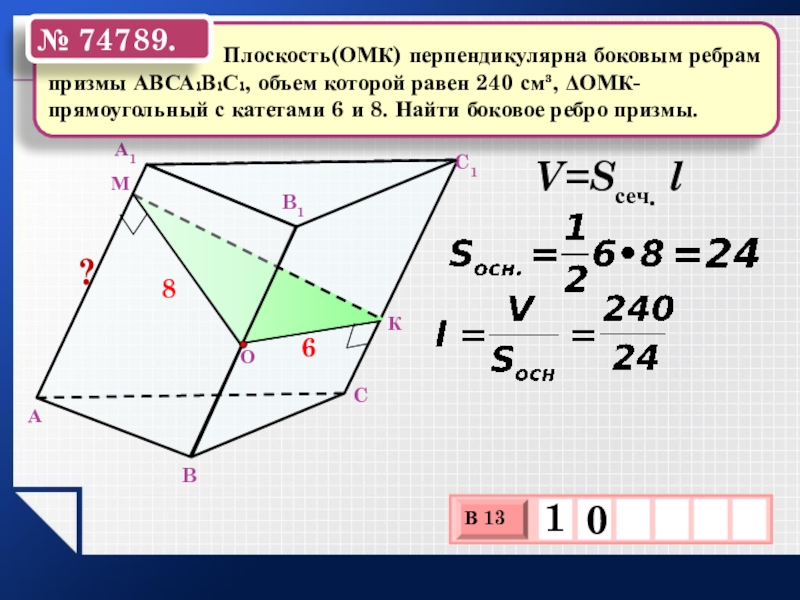
- 9. АB ?C1B1А1 C 86V=Sсеч. l
- 10. Что мы знаем о пирамиде?Презентация ученицы 11 «Б» класса Дергуновой Анны.
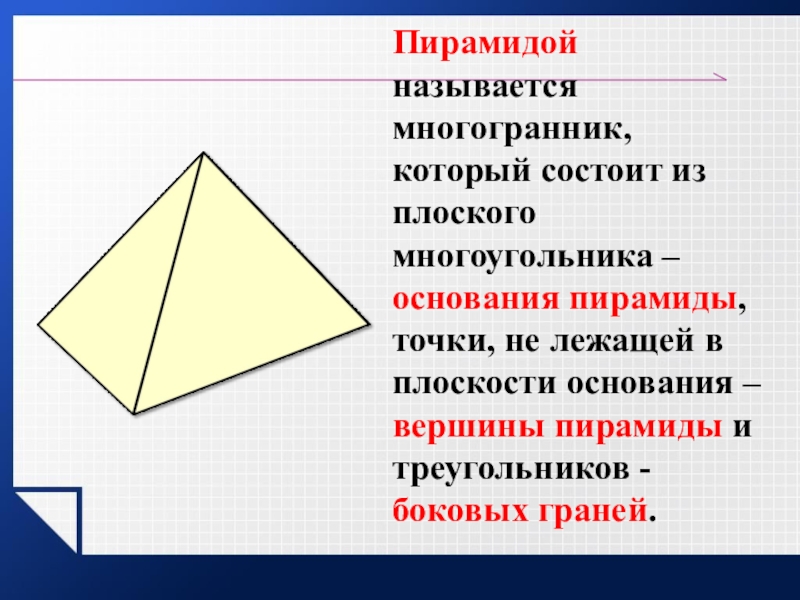
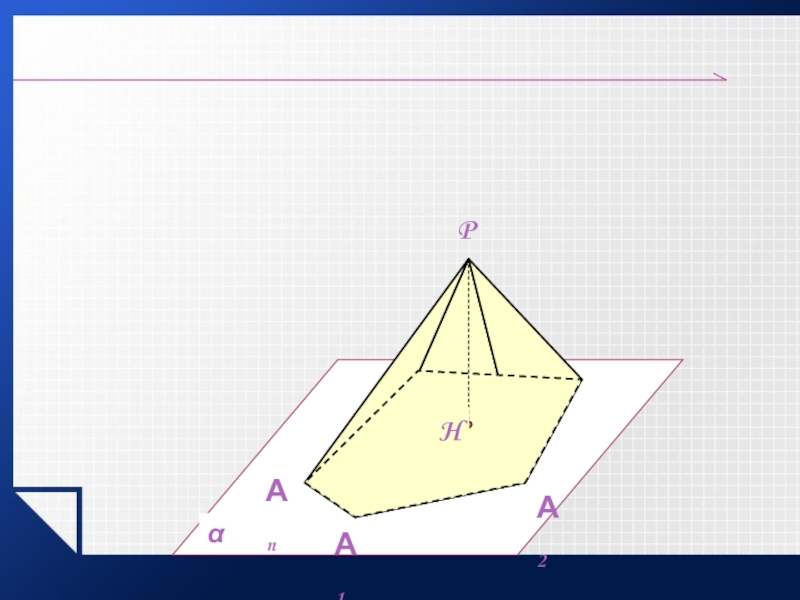
- 11. Пирамидой называется многогранник, который состоит из плоского
- 12. Термин “пирамида” заимствованиз греческого “пирамис” или “пирамидос”.
- 13. Высота Боковые ребра
- 14. ПирамидыТреугольная пирамида (тетраэдр)Шестиугольная пирамидаЧетырехугольная пирамида
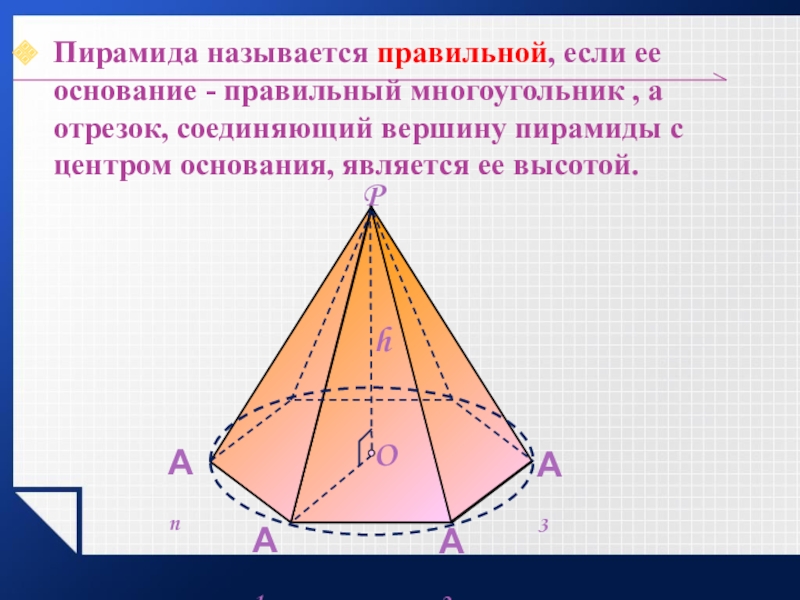
- 15. Пирамида называется правильной, если ее основание -
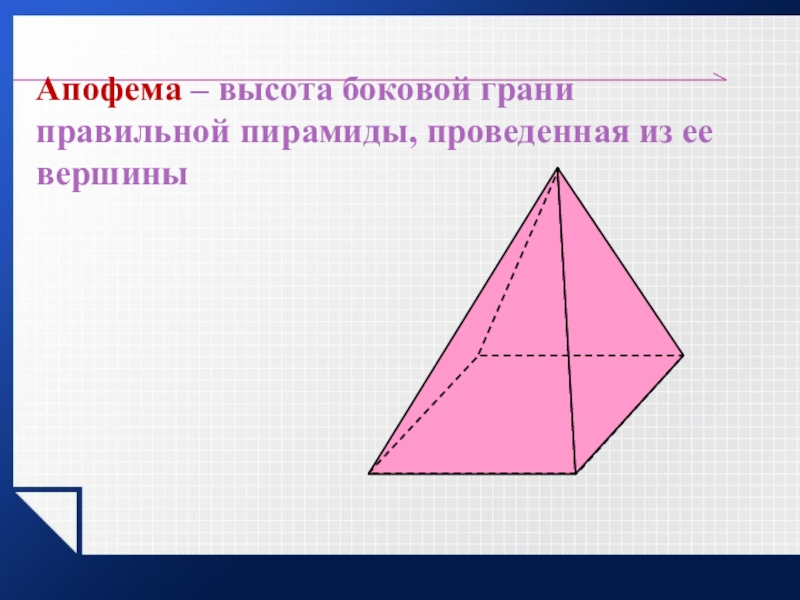
- 16. Апофема – высота боковой грани правильной пирамиды,
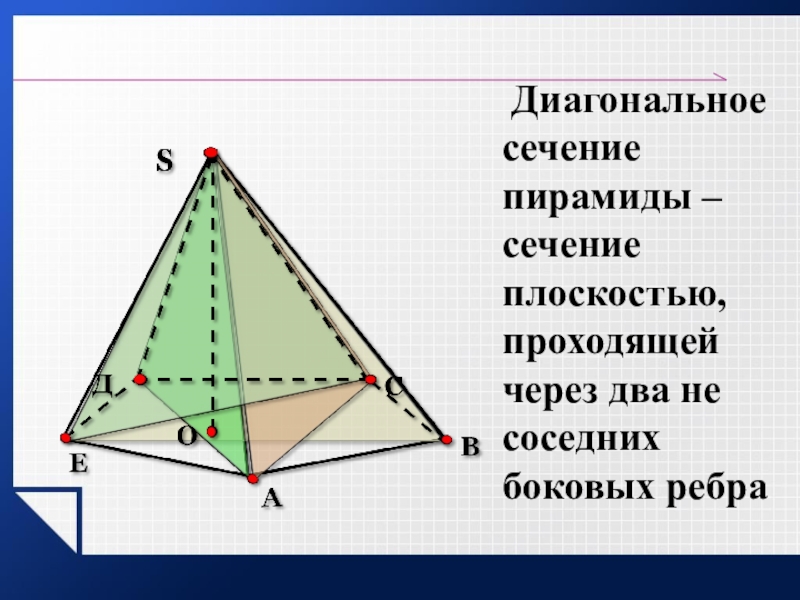
- 17. Диагональное сечение пирамиды – сечение плоскостью, проходящей через два не соседних боковых ребра
- 18. Слайд 18
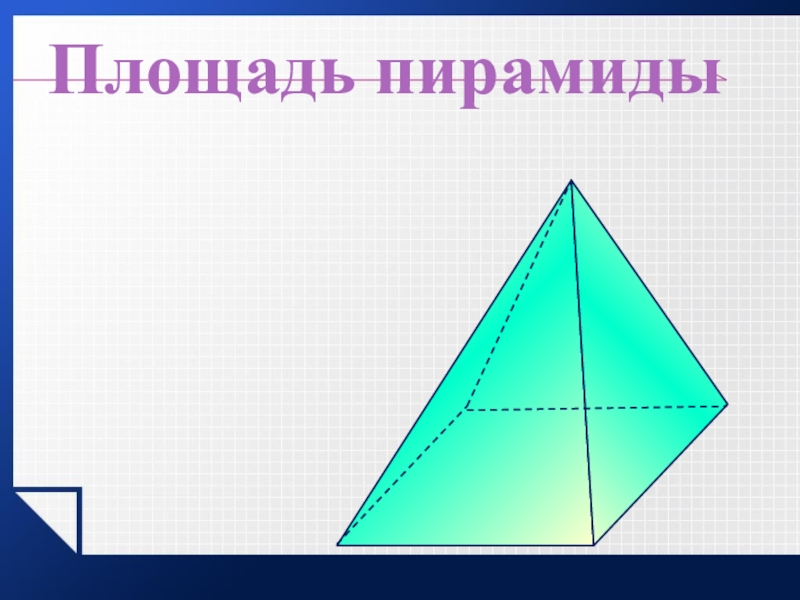
- 19. Площадь пирамидыSполн. = Sбок. + Sосн. Sбок.Sосн.
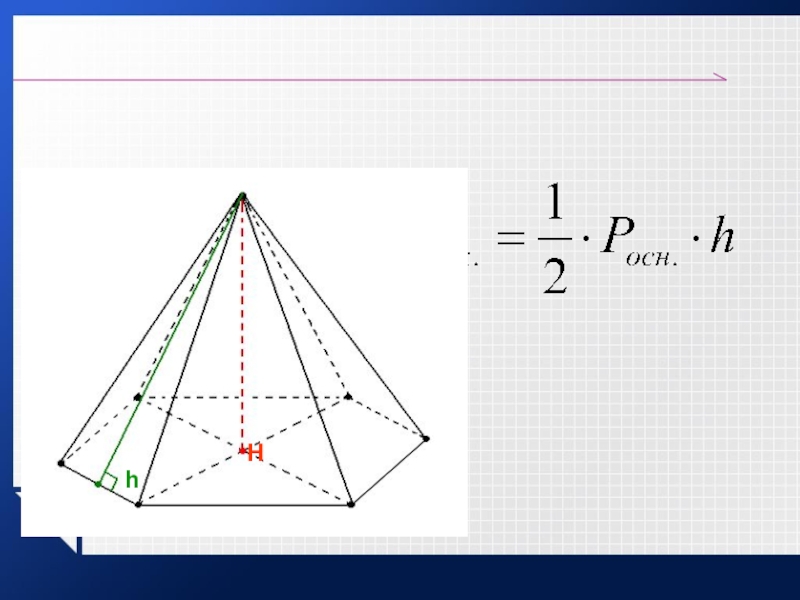
- 20. hH
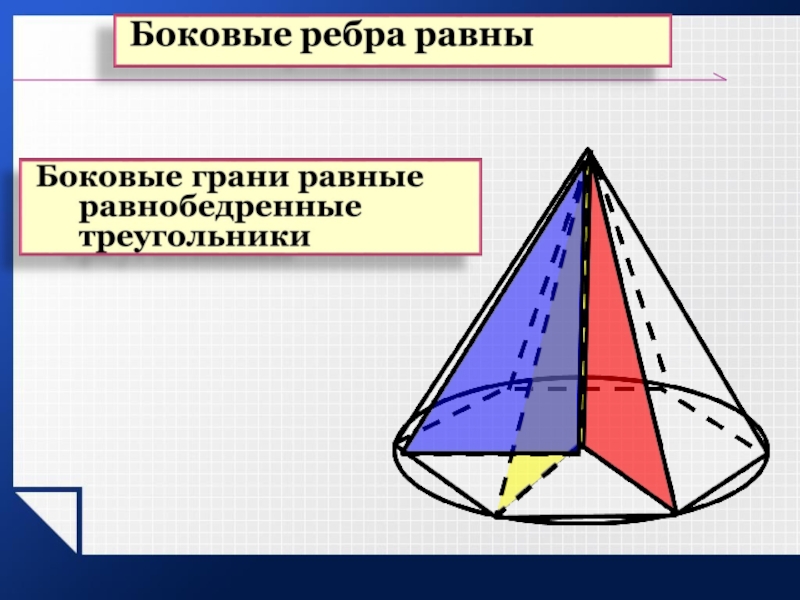
- 21. Свойства пирамиды: У правильной пирамиды:
- 22. Свойства пирамиды: если боковые ребра пирамиды
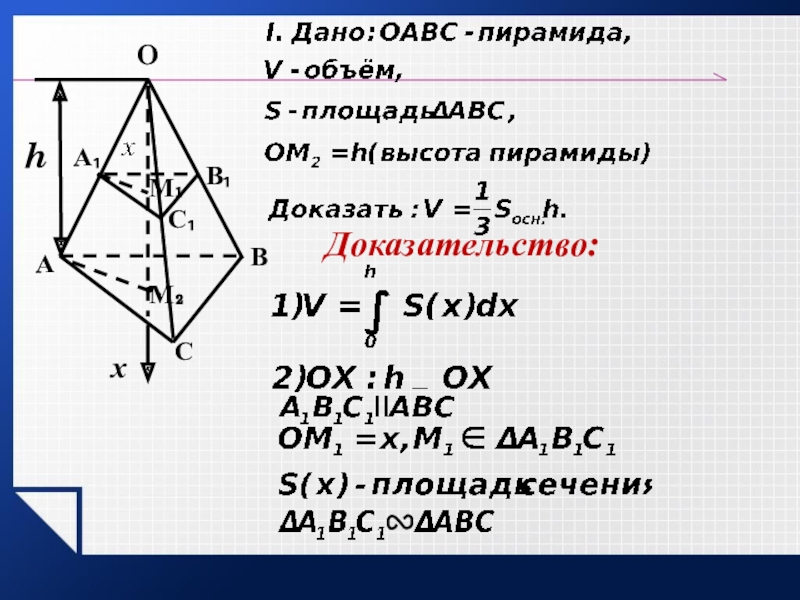
- 23. Теорема: Объём пирамиды равен одной трети произведения площади основания на высоту.∙
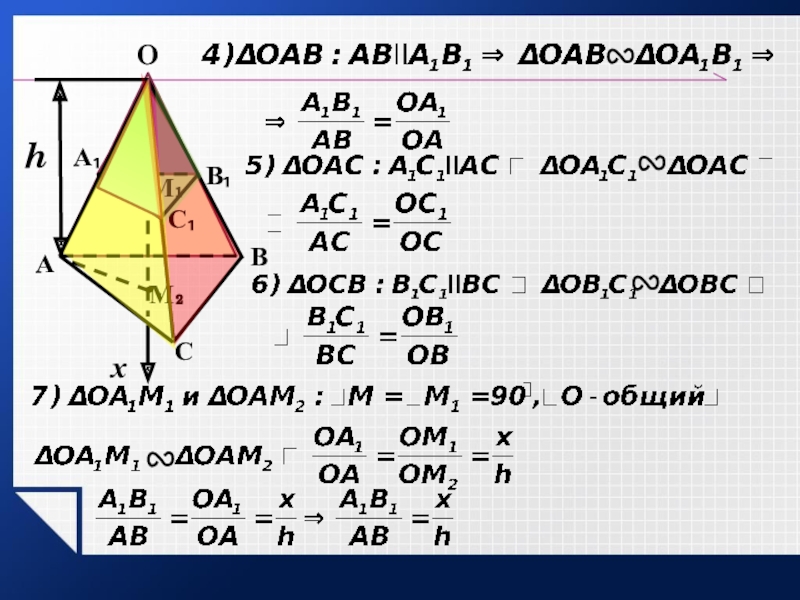
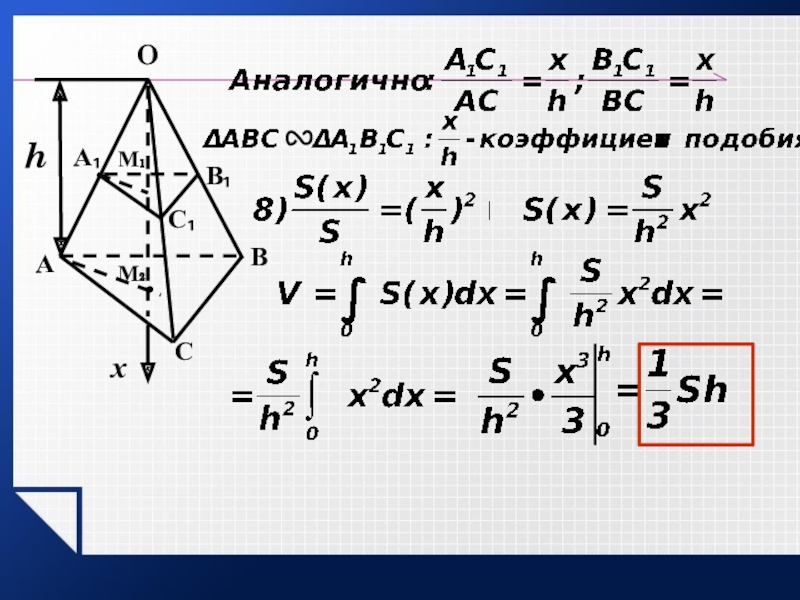
- 24. hДоказательство:OМ₂СВАхС₁А₁В₁М₁
- 25. hOМ₂СВАхС₁А₁В₁М₁
- 26. hOМ₂СВАхС₁А₁В₁М₁
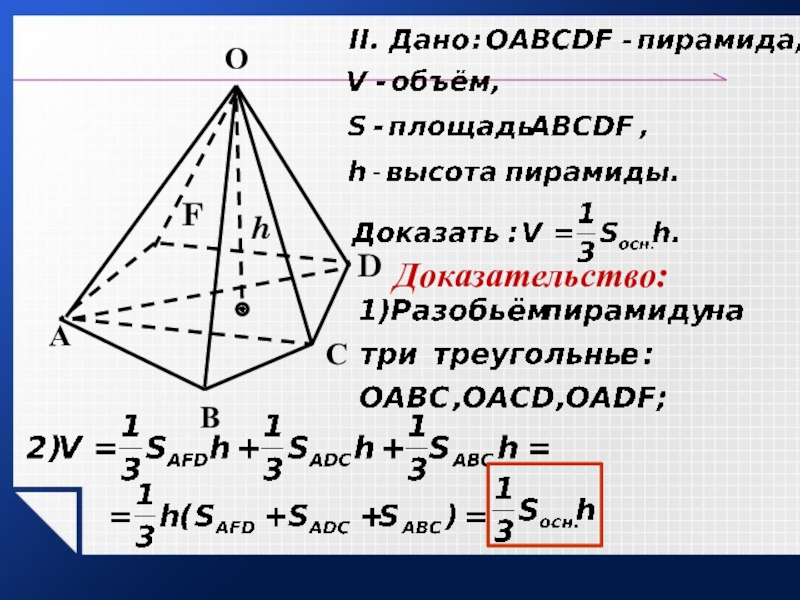
- 27. АDСВОhFДоказательство:
- 28. Слайд 28
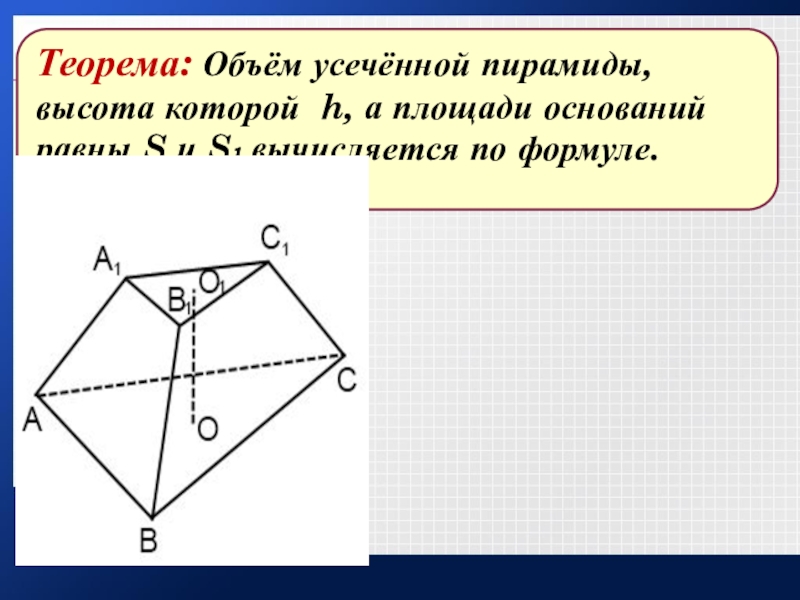
- 29. Объем усеченной пирамиды будем рассматривать как разность
- 30. Объем полной пирамиды(1)Подставляем в уравнение 1
- 31. Задачи по готовым чертежам
- 32. .Задачи по готовым чертежам В правильной четырехугольной
- 33. Сторона основания правильной треугольной
- 34. Задачи (профиль) Объем треугольной пирамиды SABC, являющейся
- 35. Домашнее задание:П. 80, № 686(а), 687.
- 36. В презентации использованы материалы сайта Савченко Е.М.
Проверка домашнего задания:
Слайд 3D1
Если плоские углы при вершине равны (в равных ромбах), то т.О
лежит на биссектрисе угла BAD.
C1
B1
A1
A
B
C
D
V = Soh
5
№ 681.
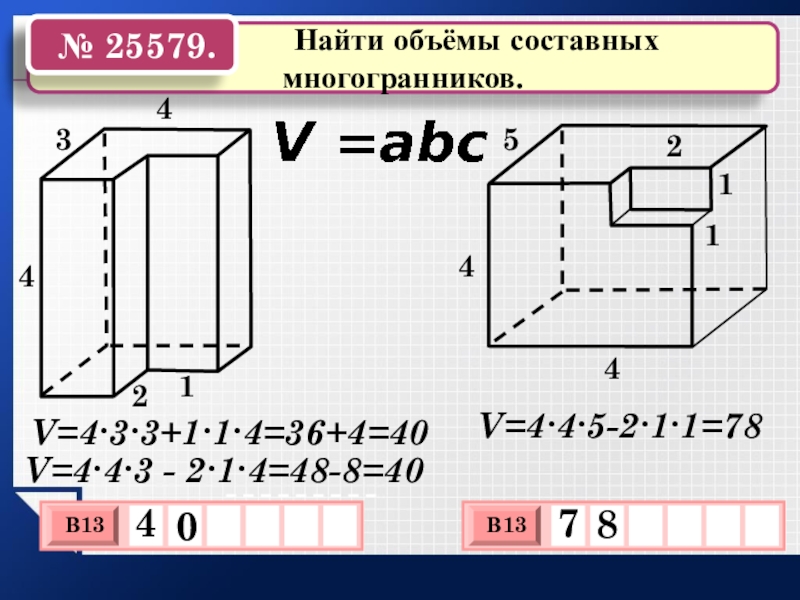
Слайд 6 Найти объёмы
составных многогранников.
4
2
1
4
3
5
2
1
1
4
4
№ 25579.
V=4∙3∙3+1∙1∙4=36+4=40
V=4∙4∙5-2∙1∙1=78
V=4∙4∙3 - 2∙1∙4=48-8=40
Слайд 75
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
№245352
Слайд 8h
V = Soснh
Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
№ 27106
Слайд 9А
B
?
C1
B1
А1
C
8
6
V=Sсеч. l
Плоскость(ОМК) перпендикулярна боковым ребрам призмы АВСА₁В₁С₁, объем которой равен 240 см³, ΔОМК- прямоугольный с катетами 6 и 8. Найти боковое ребро призмы.
№ 74789.
М
Слайд 11Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды,
точки, не лежащей в плоскости основания – вершины пирамиды и треугольников -боковых граней.
Слайд 12Термин “пирамида” заимствован
из греческого “пирамис” или “пирамидос”. Греки в свою очередь
позаимствовали это слово, как полагают, из египетского языка. В папирусе Ахмеса встречается слово “пирамус” в смысле ребра правильной пирамиды. Другие считают, что термин берет свое начало от форм хлебцев в Древней Греции “пирос” - рожь). В связи с тем, что форма пламени иногда напоминает образ пирамиды, некоторые средневековые ученые считали, что термин происходит от греческого слова “пир” - огонь. Вот почему в некоторых учебниках геометрии XVI в. пирамида названа “огнеформное тело”.
Слайд 15Пирамида называется правильной, если ее основание - правильный многоугольник , а
отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
Слайд 16Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины
Апофемы
Все апофемы правильной пирамиды равны друг другу
Слайд 17 Диагональное сечение пирамиды – сечение плоскостью, проходящей через два не
соседних боковых ребра
Слайд 21 Свойства пирамиды:
У правильной пирамиды:
боковые ребра равны;
боковые грани являются равными равнобедренными треугольниками;
апофемы равны;
площадь боковой поверхности правильной пирамиды равна половине произведения периметра на апофему.
апофемы равны;
площадь боковой поверхности правильной пирамиды равна половине произведения периметра на апофему.
Слайд 22 Свойства пирамиды:
если боковые ребра пирамиды равны (или составляют равные
углы с плоскостью основания), то вершина пирамиды проецируется в центр окружности, описанной около основания.
если двугранные углы при основании пирамиды равны (или равны высоты боковых граней, проведенные из вершины пирамиды), то вершина пирамиды проецируется в центр окружности, вписанной в основание пирамиды.
если двугранные углы при основании пирамиды равны (или равны высоты боковых граней, проведенные из вершины пирамиды), то вершина пирамиды проецируется в центр окружности, вписанной в основание пирамиды.
Слайд 29Объем усеченной пирамиды будем рассматривать как разность объемов полной пирамиды и
той, что отсечена от нее плоскостью, параллельной основанию
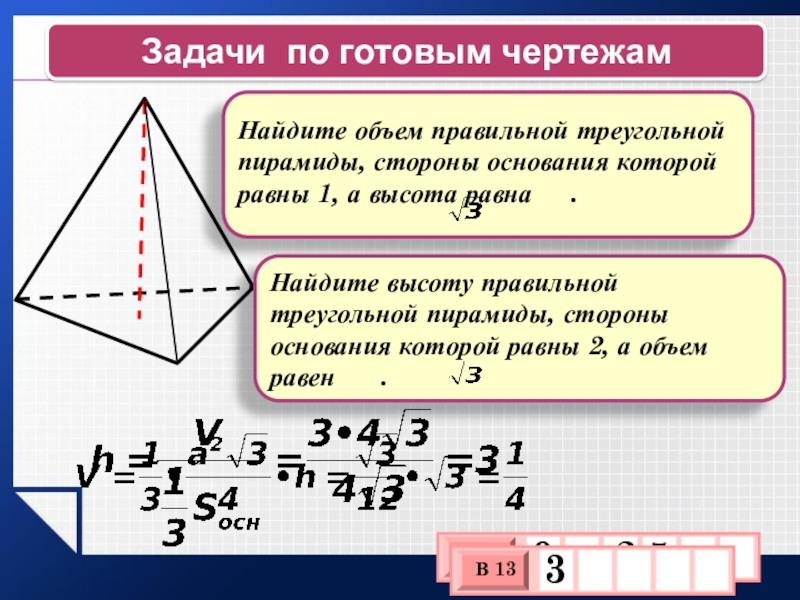
Слайд 31Задачи по готовым чертежам
Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна .
Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен .
Слайд 32.
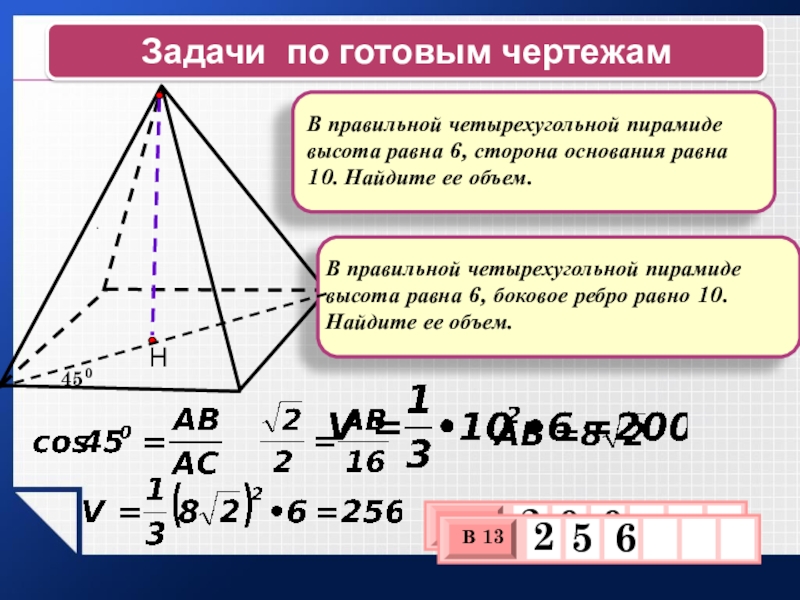
Задачи по готовым чертежам
В правильной четырехугольной пирамиде высота равна 6,
сторона основания равна 10. Найдите ее объем.
В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
450
Слайд 33 Сторона основания правильной треугольной пирамиды равна 6, а
боковое ребро образует с плоскостью основания угол 450. Найдите объем пирамиды.
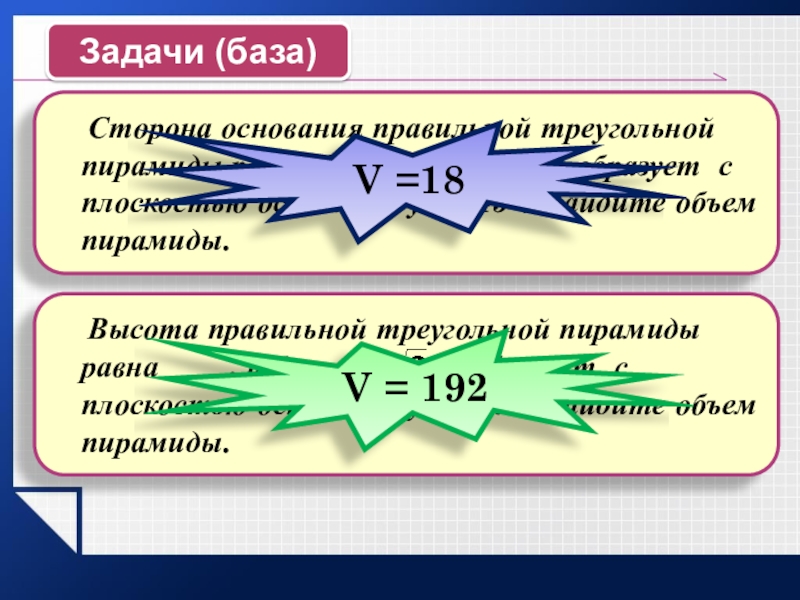
Задачи (база)
Высота правильной треугольной пирамиды равна , а боковая грань образует с плоскостью основания угол 600. Найдите объем пирамиды.
V = 192
V =18
Слайд 34Задачи (профиль)
Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды
SABCDEF, равен 8. Найдите объем шестиугольной пирамиды.
От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания.
Найдите объем отсеченной треугольной пирамиды.
V = 48
V =3
