- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Многогранники
Содержание
- 1. Презентация по математике на тему Многогранники
- 2. Тематический план:Многогранники.Прямоугольный параллелепипед. Куб.Построение сечений в прямоугольном
- 3. МногогранникиЭто тела, поверхности которых состоят из конечного числа многоугольников
- 4. Параллелепипед- многогранник, который состоит из двух плоских
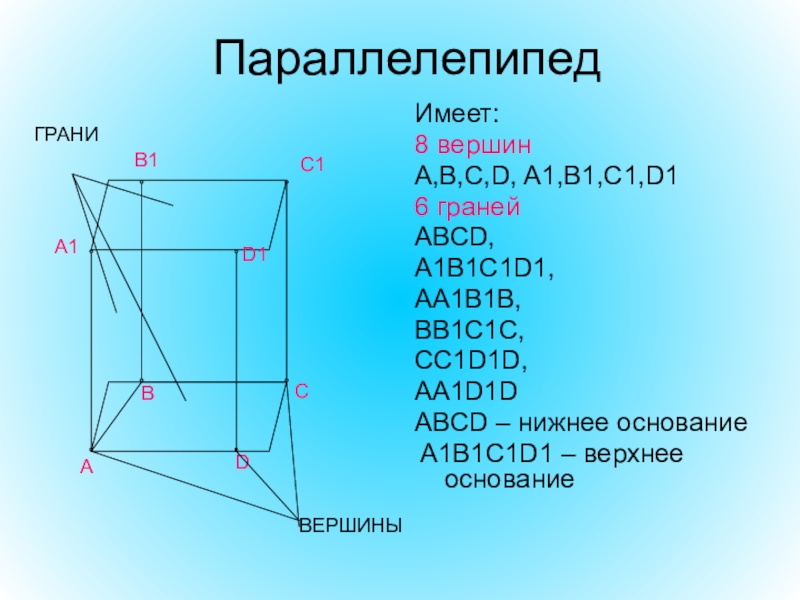
- 5. ПараллелепипедИмеет:8 вершин А,B,C,D, A1,B1,C1,D16 граней ABCD,
- 6. ПараллелепипедТеорема: У параллелепипеда противоположные грани параллельны и равны
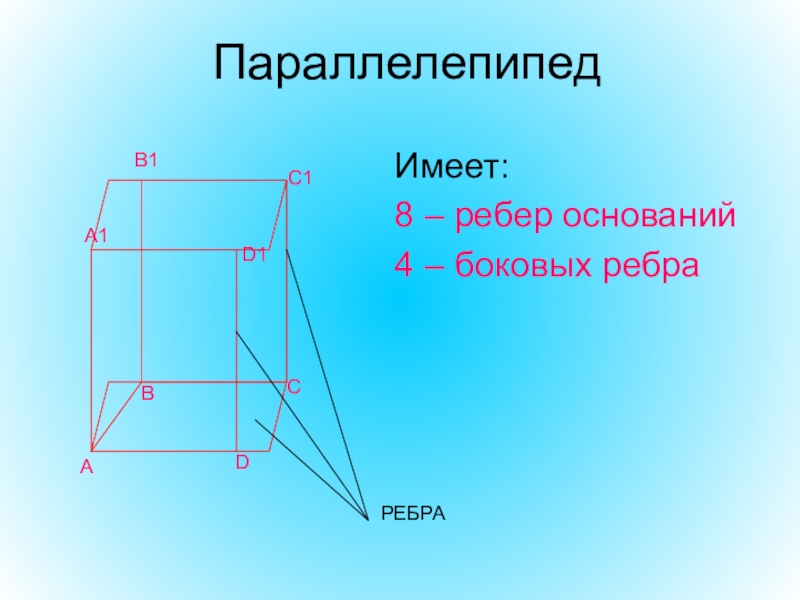
- 7. Имеет:8 – ребер оснований4 – боковых ребра ПараллелепипедBCADA1B1C1D1РЕБРА
- 8. Высотой называется перпендикуляр опущенный из вершины верхнего
- 9. У наклонного параллелепипеда – это перпендикуляр, опущенный из вершины верхнего основания на плоскость нижнего основания. Параллелепипедh
- 10. Прямоугольный параллелепипедДиагонали основанийа,b,c – линейные размеры (измерения)abc
- 11. Прямоугольный параллелепипедДиагонали прямоугольного параллелепипеда – отрезки, соединяющие
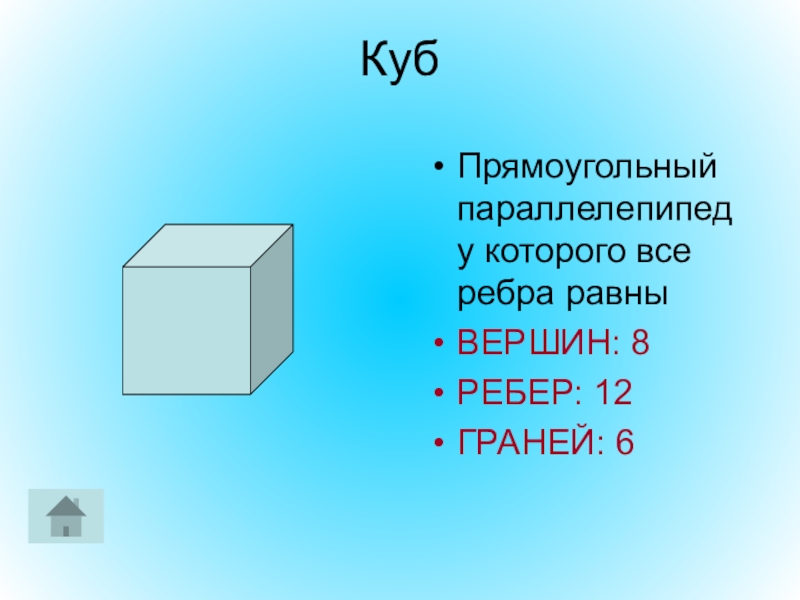
- 12. КубПрямоугольный параллелепипед у которого все ребра равныВЕРШИН: 8РЕБЕР: 12ГРАНЕЙ: 6
- 13. Построение сечений в прямоугольном параллелепипеде и кубе.
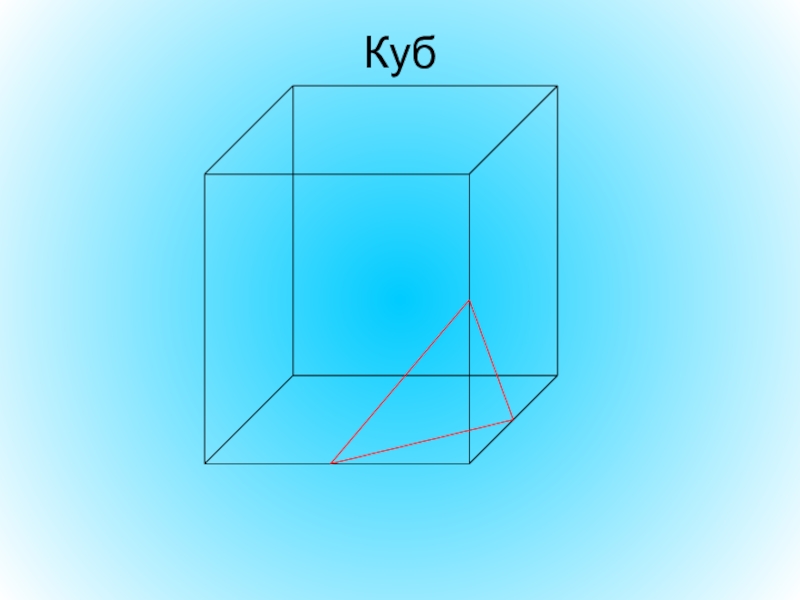
- 14. Постройте плоскость сечения куба так, чтобы получился:Правильный треугольник
- 15. Куб
- 16. Куб
- 17. Равнобедренный треугольник
- 18. Куб
- 19. Куб
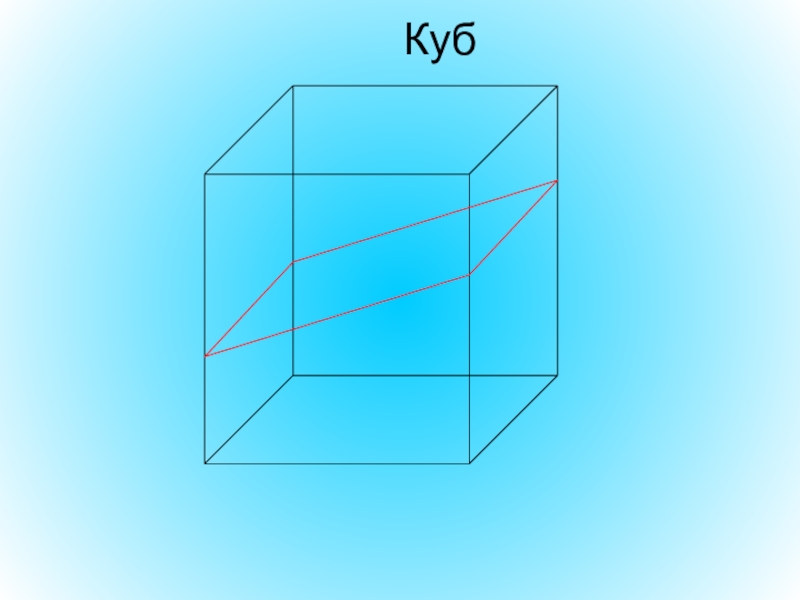
- 20. Квадрат
- 21. КубСечение плоскостью
- 22. Куб
- 23. Прямоугольник
- 24. Куб
- 25. Куб
- 26. Куб
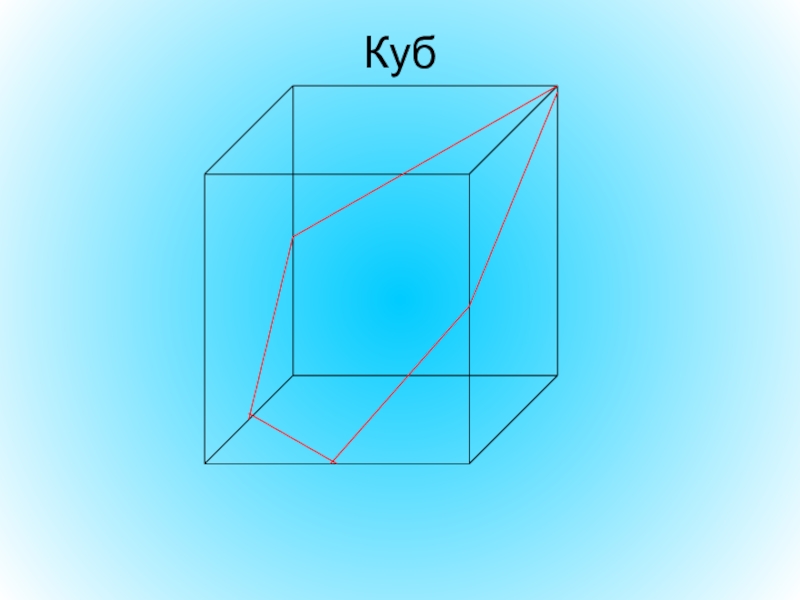
- 27. Трапеция
- 28. Куб
- 29. Правильный пятиугольник
- 30. Куб
- 31. Правильный шестиугольник
- 32. Куб
- 33. Слайд 33
- 34. Математический диктантИзобразите параллелепипедДайте определение, что называется параллелепипедомСколько
- 35. Призма -многогранник, который состоит из двух плоских
- 36. Треугольная призма6 – вершин5 – граней9 - реберАBCA1B1C1
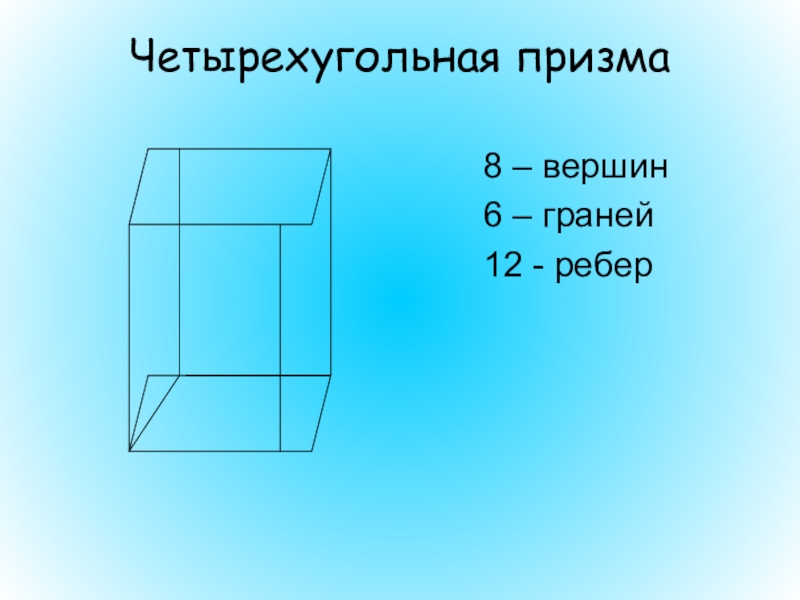
- 37. Четырехугольная призма8 – вершин6 – граней12 - ребер
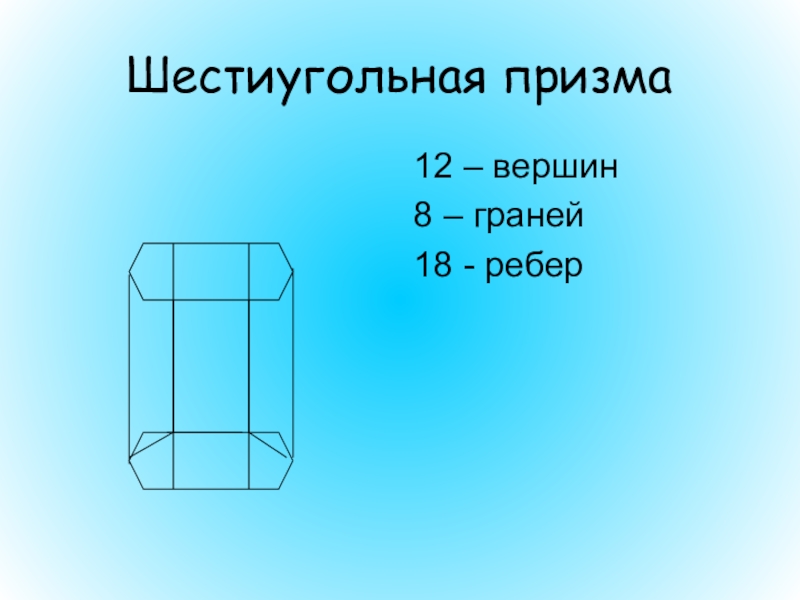
- 38. Шестиугольная призма12 – вершин8 – граней18 - ребер
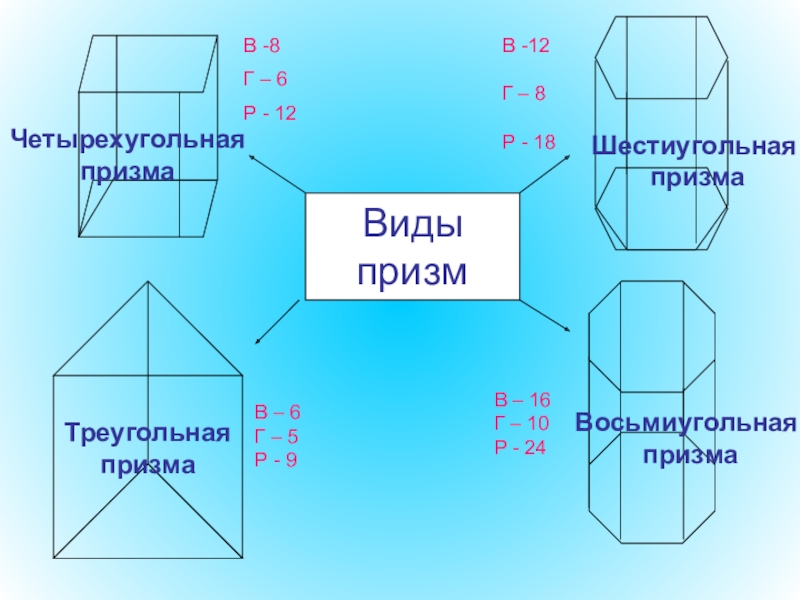
- 39. Виды призм В -8Г – 6Р -
- 40. Призма называется правильной, если в ее основании
- 41. Призма называется прямой, если ее боковые ребра
- 42. Пирамида –многогранник, который состоит из плоского многоугольника
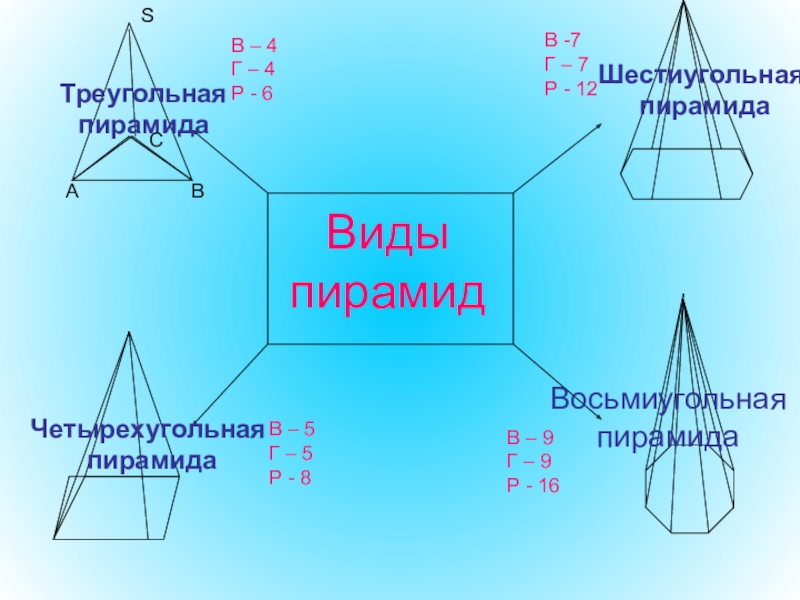
- 43. Виды пирамидТреугольная пирамидаЧетырехугольная пирамидаШестиугольная пирамидаВосьмиугольная пирамидаВ –
- 44. Пирамида называется правильной, если в ее основании
- 45. Высотой призмы называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.Апофема – высота боковой грани
- 46. Усеченная пирамида
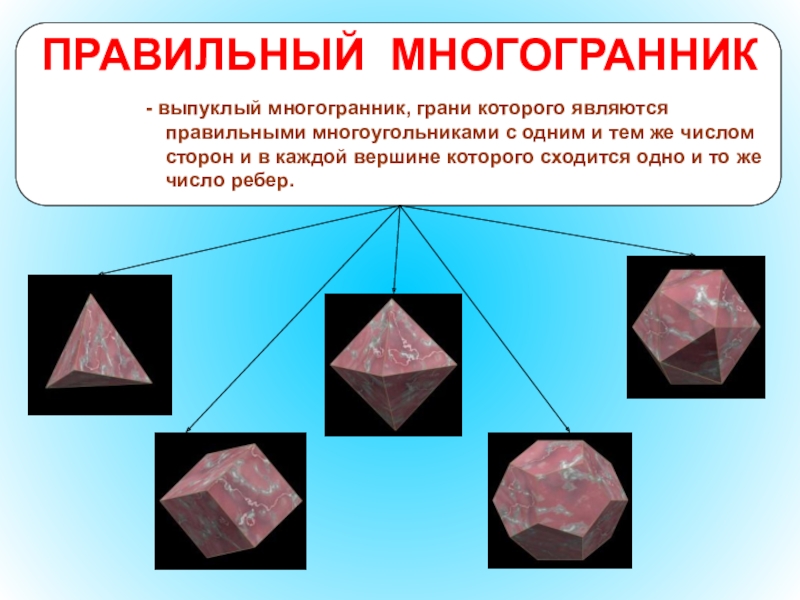
- 47. ПРАВИЛЬНЫЙ МНОГОГРАННИК- выпуклый многогранник, грани которого являются
- 48. Названия многогранников пришли из Древней Греции, в
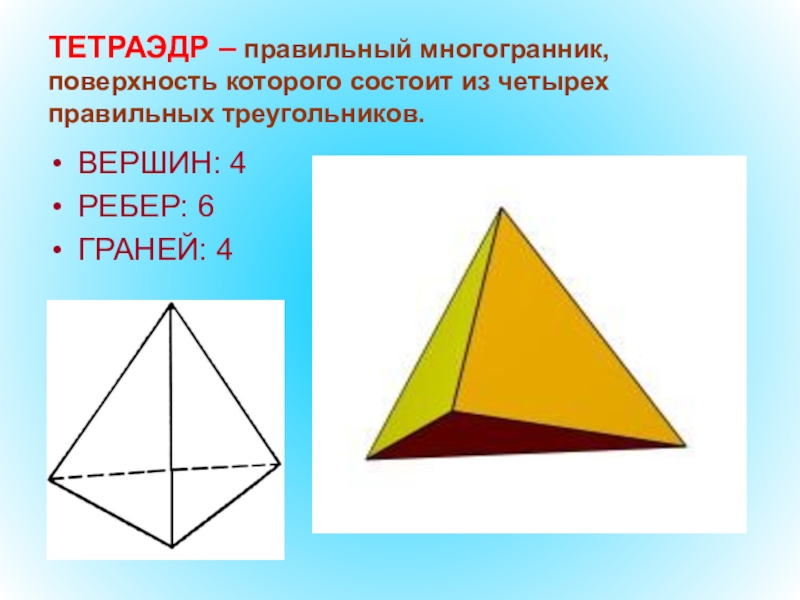
- 49. ТЕТРАЭДР – правильный многогранник, поверхность которого состоит из четырех правильных треугольников.ВЕРШИН: 4РЕБЕР: 6ГРАНЕЙ: 4
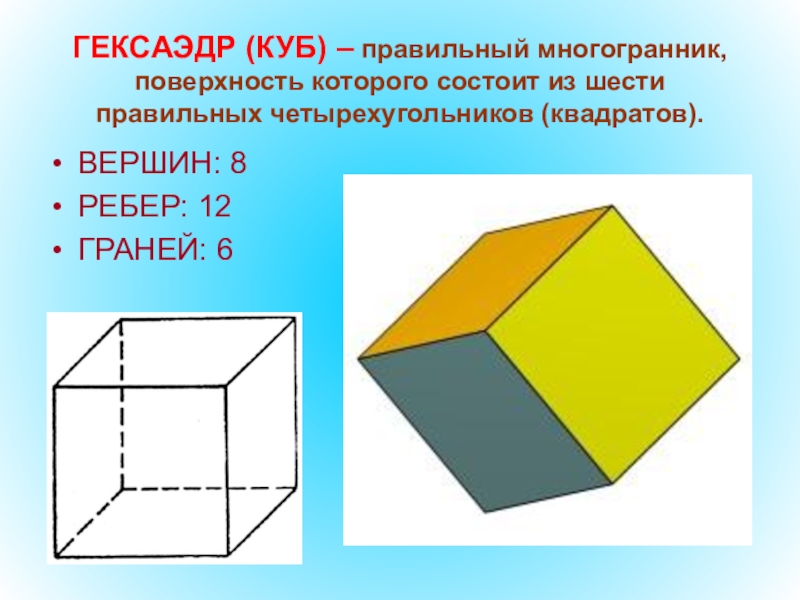
- 50. ГЕКСАЭДР (КУБ) – правильный многогранник, поверхность которого состоит из шести правильных четырехугольников (квадратов).ВЕРШИН: 8РЕБЕР: 12ГРАНЕЙ: 6
- 51. ОКТАЭДР – правильный многогранник, поверхность которого состоит из восьми правильных треугольников.ВЕРШИН: 6РЕБЕР: 12ГРАНЕЙ: 8
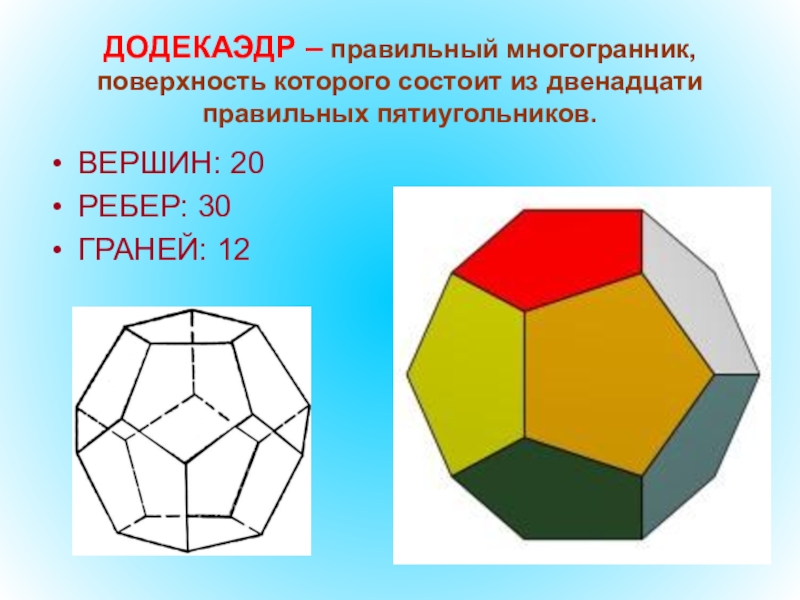
- 52. ДОДЕКАЭДР – правильный многогранник, поверхность которого состоит из двенадцати правильных пятиугольников.ВЕРШИН: 20РЕБЕР: 30ГРАНЕЙ: 12
- 53. ИКОСАЭДР – правильный многогранник, поверхность которого состоит из двадцати правильных треугольников.ВЕРШИН: 12РЕБЕР: 30ГРАНЕЙ: 20
- 54. Число граней плюс число вершин минус число
- 55. Построение разверток многогранников
- 56. Разверткой многогранника называется фигура на плоскости,
- 57. КУБ
- 58. Прямоугольный параллелепипед
- 59. Правильная треугольная призма
- 60. Правильная четырехугольная призма
- 61. Правильная шестиугольная призма
- 62. Правильная восьмиугольная призма
- 63. Правильная треугольная пирамида
- 64. Правильная четырехугольная пирамида
- 65. Многогранники вокруг нас
- 66. Многогранные формы окружают нас повсюду. Почти все
- 67. МногогранникиКуб ОктаэдрТетраэдр ИкосаэдрДодекаэдр
- 68. Многогранники
- 69. Египетские пирамидыТайна Пирамид в различных частях Света
- 70. Египетские пирамиды Полученные инженером Давидсоном результаты измерения
- 71. Египетские пирамиды.Таким образом, за 2500лет до Р.Х.
- 72. Пирамиды современностиКомпания АБО осуществляет проекты по строительству
- 73. Пирамиды современностиЗа последние годы компанией АБО были
- 74. Пчелиные сотыПчели́ные со́ты — восковые постройки пчёл,
- 75. Многогранники в кулинарии Многогранники в кулинарии применяются
- 76. Формы нарезки картофеля
- 77. Формы нарезки моркови, свеклы, репы
- 78. Формы нарезки капусты
- 79. Кулинария
- 80. Кулинария
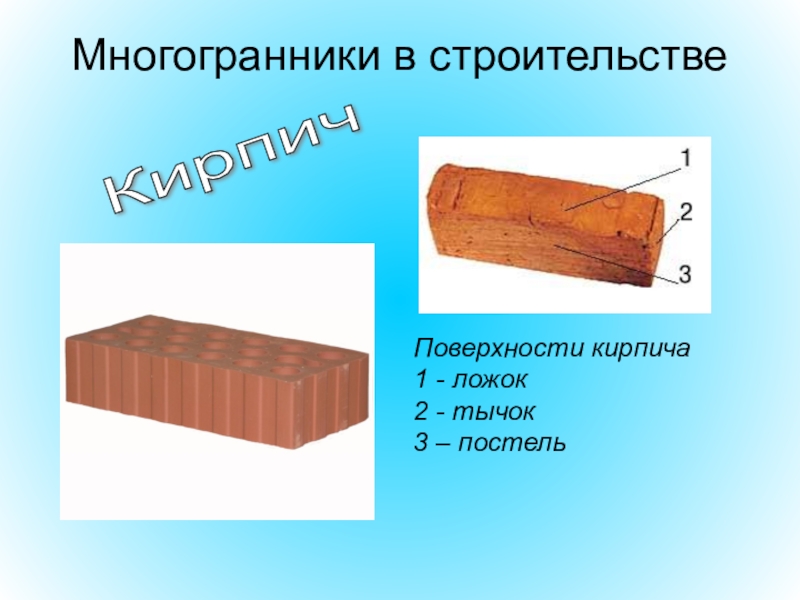
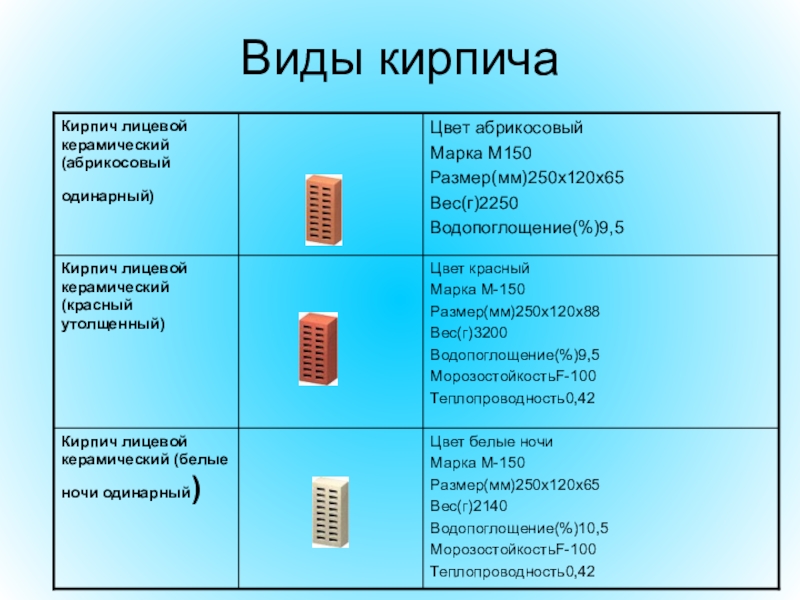
- 81. Многогранники в строительствеКирпичПоверхности кирпича 1 - ложок 2 - тычок 3 – постель
- 82. Виды кирпича
- 83. Многогранники в строительстве
- 84. «Тайная вечеря»Сальвадор Дали
- 85. Правильные многогранники встречаются в живой природе. Например,
- 86. Правильные многогранники – самые «выгодные» фигуры. И
Тематический план:Многогранники.Прямоугольный параллелепипед. Куб.Построение сечений в прямоугольном параллелепипеде и кубе.Призма. Построение сечений в призмах.Пирамида. Построение сечений в пирамиде.Правильные многогранники. Моделирование многогранников.Звездчатые многогранники. Полуправильные многогранники.Графическая работа «Многогранники»Многогранники вокруг нас.Зачет «Многогранники»
Слайд 2Тематический план:
Многогранники.
Прямоугольный параллелепипед. Куб.
Построение сечений в прямоугольном параллелепипеде и кубе.
Призма.
Построение
сечений в призмах.
Пирамида. Построение сечений в пирамиде.
Правильные многогранники. Моделирование многогранников.
Звездчатые многогранники. Полуправильные многогранники.
Графическая работа «Многогранники»
Многогранники вокруг нас.
Зачет «Многогранники»
Пирамида. Построение сечений в пирамиде.
Правильные многогранники. Моделирование многогранников.
Звездчатые многогранники. Полуправильные многогранники.
Графическая работа «Многогранники»
Многогранники вокруг нас.
Зачет «Многогранники»
Слайд 4Параллелепипед
- многогранник, который состоит из двух плоских многоугольников, лежащих в разных
плоскостях и отрезков соединяющих вершины этих многоугольников
B
C
A
D
A1
B1
C1
D1
Слайд 5 Параллелепипед
Имеет:
8 вершин
А,B,C,D, A1,B1,C1,D1
6 граней
ABCD,
A1B1C1D1,
AA1B1B,
BB1C1C,
CC1D1D,
AA1D1D
ABCD – нижнее основание
A1B1C1D1 – верхнее основание
B
C
A
D
A1
B1
C1
D1
ВЕРШИНЫ
ГРАНИ
Слайд 8
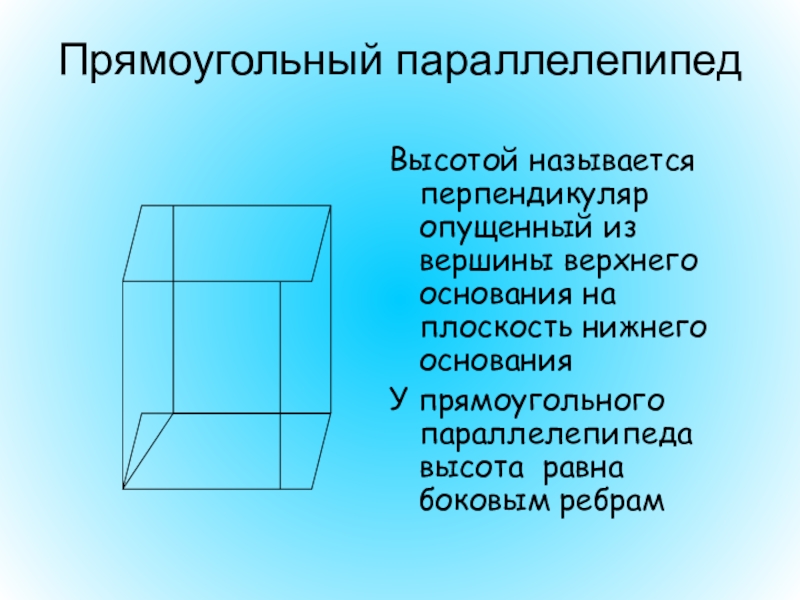
Высотой называется перпендикуляр опущенный из вершины верхнего основания на плоскость нижнего
основания
У прямоугольного параллелепипеда высота равна боковым ребрам
У прямоугольного параллелепипеда высота равна боковым ребрам
Прямоугольный параллелепипед
Слайд 9У наклонного параллелепипеда
– это перпендикуляр, опущенный из вершины верхнего основания
на плоскость нижнего основания.
Параллелепипед
h
Слайд 11Прямоугольный параллелепипед
Диагонали прямоугольного параллелепипеда – отрезки, соединяющие две вершины, не принадлежащие
одной грани
Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам
Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам
а
b
c
Слайд 34Математический диктант
Изобразите параллелепипед
Дайте определение, что называется параллелепипедом
Сколько вершин у параллелепипеда
Сколько граней
и ребер имеет параллелепипед.
Дайте определение высоты параллелепипеда.
Дайте определение куба и перечислите сколько ребер, вершин, граней.
Изобразите три различных параллелепипеда и три куба.
Дайте определение высоты параллелепипеда.
Дайте определение куба и перечислите сколько ребер, вершин, граней.
Изобразите три различных параллелепипеда и три куба.
Слайд 35Призма -многогранник, который состоит из двух плоских многоугольников, лежащих в разных
плоскостях и отрезков соединяющих вершины этих многоугольников
Слайд 39Виды
призм
В -8
Г – 6
Р - 12
В -12
Г – 8
Р
- 18
В – 6
Г – 5
Р - 9
Треугольная призма
Четырехугольная призма
Шестиугольная
призма
Восьмиугольная
призма
В – 16
Г – 10
Р - 24
Слайд 40Призма называется правильной, если в ее основании лежит правильный многоугольник (
у четырехугольной призмы – квадрат, у треугольной призмы – равносторонний треугольник, у шестиугольной призмы – правильный шестиугольник)
Слайд 41Призма называется прямой, если ее боковые ребра перпендикулярны основанию.
Высотой призмы называется
расстояние между плоскостями оснований.
Диагональю призмы называется отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.
Диагональю призмы называется отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.
h
d
Слайд 42Пирамида –многогранник, который состоит из плоского многоугольника – основания пирамиды, точки
не лежащей в плоскости основания – вершины пирамиды, и всех отрезков, соединяющих вершину пирамиды с точками основания.
Слайд 43
Виды пирамид
Треугольная
пирамида
Четырехугольная
пирамида
Шестиугольная
пирамида
Восьмиугольная
пирамида
В – 5
Г – 5
Р -
8
В – 9
Г – 9
Р - 16
В – 4
Г – 4
Р - 6
В -7
Г – 7
Р - 12
А
B
C
S
Слайд 44Пирамида называется правильной, если в ее основании лежит правильный многоугольник (
у четырехугольной призмы – квадрат, у треугольной призмы – равносторонний треугольник, у шестиугольной призмы – правильный шестиугольник)
Слайд 45Высотой призмы называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Апофема
– высота боковой грани
Слайд 47
ПРАВИЛЬНЫЙ МНОГОГРАННИК
- выпуклый многогранник, грани которого являются правильными многоугольниками с одним
и тем же числом сторон и в каждой вершине которого сходится одно и то же число ребер.
Слайд 48Названия многогранников пришли из Древней Греции,
в них указывается число граней:
«эдра»
− грань;
«тетра» − 4;
«гекса» − 6;
«окта» − 8;
«икоса» − 20;
«додека» − 12.
«тетра» − 4;
«гекса» − 6;
«окта» − 8;
«икоса» − 20;
«додека» − 12.
Слайд 49ТЕТРАЭДР – правильный многогранник, поверхность которого состоит из четырех правильных треугольников.
ВЕРШИН:
4
РЕБЕР: 6
ГРАНЕЙ: 4
РЕБЕР: 6
ГРАНЕЙ: 4
Слайд 50ГЕКСАЭДР (КУБ) – правильный многогранник, поверхность которого состоит из шести правильных
четырехугольников (квадратов).
ВЕРШИН: 8
РЕБЕР: 12
ГРАНЕЙ: 6
Слайд 51ОКТАЭДР – правильный многогранник, поверхность которого состоит из восьми правильных треугольников.
ВЕРШИН:
6
РЕБЕР: 12
ГРАНЕЙ: 8
РЕБЕР: 12
ГРАНЕЙ: 8
Слайд 52ДОДЕКАЭДР – правильный многогранник, поверхность которого состоит из двенадцати правильных пятиугольников.
ВЕРШИН:
20
РЕБЕР: 30
ГРАНЕЙ: 12
РЕБЕР: 30
ГРАНЕЙ: 12
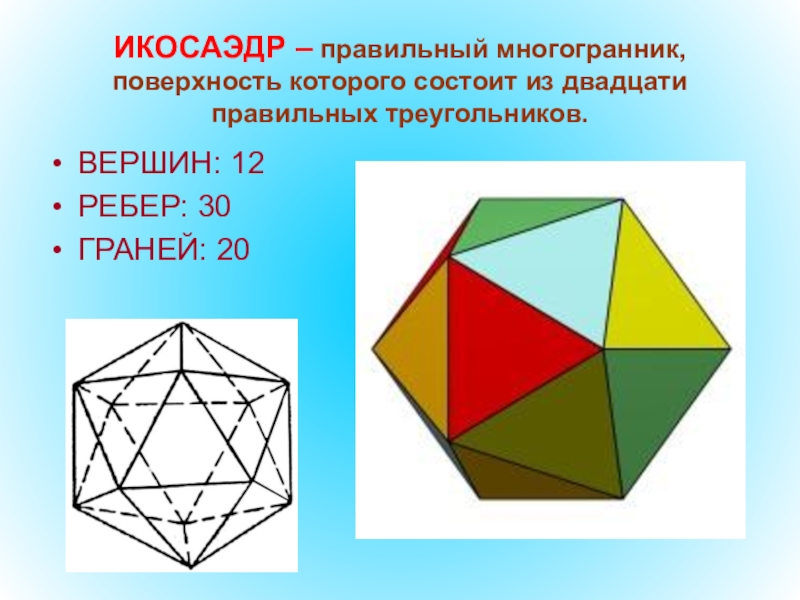
Слайд 53ИКОСАЭДР – правильный многогранник, поверхность которого состоит из двадцати правильных треугольников.
ВЕРШИН:
12
РЕБЕР: 30
ГРАНЕЙ: 20
РЕБЕР: 30
ГРАНЕЙ: 20
Слайд 54
Число граней плюс число вершин минус число рёбер в любом многограннике
равно 2.
Г + В − Р = 2
Г + В − Р = 2
Формула Эйлера
Слайд 56Разверткой многогранника называется фигура на плоскости, полученная путем разрезания по
некоторым ребрам и развернута, так чтобы все многоугольники лежали в одной плоскости.
Слайд 66Многогранные формы окружают нас повсюду. Почти все сооружения, возведённые человеком, от
древнеегипетских пирамид до современных небоскрёбов, имеют форму многогранников. Многогранные формы встречаются у многих минералов и, что особенно удивительно, у некоторых растений и даже живых организмов.
Слайд 69Египетские пирамиды
Тайна Пирамид в различных частях Света интересует многих. Загадки Пирамиды
часто также интересны, как и сложны. Не секрет, что Египетские Пирамиды в Гизе (особенно Пирамида Хеопса) пользуются большой популярностью в мире.
Слайд 70Египетские пирамиды
Полученные инженером Давидсоном
результаты измерения египетской
пирамиды Хеопса оказались
поразительными.
Диагональ египетской пирамиды Хеопса дает
абсолютно точное ее направление по
меридиану, причем точность этого
направления на теоретический северный
полюс достигает 4 минуты 30 секунд: это
точнее, чем Парижская обсерватория.
Кроме того, этот меридиан, проходящий
через египетскую пирамиду Хеопса, делит
на две равные части поверхность
моря и суши, считая Америку и
Тихий океан. Более того: широта,
проходящая через центр пирамиды
Хеопса, делит также на две равные
части весь земной шар, по количеству
суши и воды.
Диагональ египетской пирамиды Хеопса дает
абсолютно точное ее направление по
меридиану, причем точность этого
направления на теоретический северный
полюс достигает 4 минуты 30 секунд: это
точнее, чем Парижская обсерватория.
Кроме того, этот меридиан, проходящий
через египетскую пирамиду Хеопса, делит
на две равные части поверхность
моря и суши, считая Америку и
Тихий океан. Более того: широта,
проходящая через центр пирамиды
Хеопса, делит также на две равные
части весь земной шар, по количеству
суши и воды.
Слайд 71Египетские пирамиды.
Таким образом, за 2500лет до Р.Х. египтяне
знали точное соотношение
поверхности всех материков и н
е случайно выбрали устье Нила для
постройки египетских пирамид Гизы.
При измерении самой пирамиды Хеопса оказалось,
что периметр пирамиды Гизы, разделенный на
двойную высоту, дает точное число «Пи»,
с точностью до одной стотысячной.
Интересно, что священная мера длины Египта,
т.е. пирамидальный дюйм (по странному
совпадению равный современному английскому)
есть одна миллиардная часть орбиты Земли,
пройденной ею в 24 часа. Другая линейная
мера пирамиды - локоть, равная 25 дюймам,
или 635,66 миллиметра - это одна
десятимиллионная полярного радиуса Земли.
Сумма двух диагоналей египетской пирамиды,
выраженных в дюймах, дает число лет,
в течение которых северный полюс
нашей земли совершает один полный оборот.
Объем пирамиды, помноженный на удельный
вес камня, из которого она сделана, дает
теоретический вес земного шара.
Слайд 72Пирамиды современности
Компания АБО осуществляет проекты по строительству Пирамид высотой 5,5; 11,
22 метра, а также других размеров с соблюдением пропорций Золотого Сечения и правил строительства. Пирамиды Александра Голода строятся для улучшения экологической обстановки в различных регионах, для использования в лечебно-оздоровительном процессе, для повышения привлекательности коммерческих объектов (пансионатов, открытых кафе, домов, коттеджных поселков и т.п.).
Слайд 73Пирамиды современности
За последние годы компанией АБО были построены Пирамиды в различных
российских городах, в странах ближнего и дальнего зарубежья. Среди них:
- Пирамида высотой 11 метров на частной территории в Ницце (Франция);
- несколько Пирамид высотой 22 и 11 метров по заказу Астраханского подразделения "Газпрома" (для решения экологических проблем вблизи газоконденсатного месторождения и на оздоровительных базах);
- Пирамиды высотой 11 метров в пансионатах, санаториях, парковых зонах
- Пирамида высотой 11 метров на частной территории в Ницце (Франция);
- несколько Пирамид высотой 22 и 11 метров по заказу Астраханского подразделения "Газпрома" (для решения экологических проблем вблизи газоконденсатного месторождения и на оздоровительных базах);
- Пирамиды высотой 11 метров в пансионатах, санаториях, парковых зонах
Слайд 74Пчелиные соты
Пчели́ные со́ты — восковые постройки пчёл, предназначенные для хранения запасов
корма (мёда и перги) и выращивания потомства; являются также гнездом пчелиной семьи. Пчелиные соты состоят из шестигранных призматических ячеек, расположенных по обе стороны от общего средостения, которое может быть искусственным. В пчелиных сотах различают ячейки разных типов: пчелиные, трутневые, переходные и маточники. Размер сот зависит от формы и величины стандартной рамки улья. В улье соты расположены вертикально. Заполненные мёдом соты в стандартных рамках содержат до 4 кг мёда. Пространство для прохода пчёл между сотами называется улочкой, его стандартная ширина равна 12—13 мм.
Слайд 75Многогранники в кулинарии
Многогранники в кулинарии применяются в нарезке и в
формах готовых блюд и в выпечке.
Слайд 85Правильные многогранники встречаются в живой природе. Например, скелет одноклеточного организма феодарии
(Circjgjnia icosahtdra) по форме напоминает икосаэдр
Чем же вызвана такая природная геометризация феодарий? По-видимому, тем, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.
Чем же вызвана такая природная геометризация феодарий? По-видимому, тем, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.
Феодария
(Circjgjnia icosahtdra)
Слайд 86Правильные многогранники – самые «выгодные» фигуры. И природа этим широко пользуется.
Подтверждением тому служит форма некоторых кристаллов.
Взять хотя бы поваренную соль, без которой мы не можем обойтись. Известно, что она растворима в воде, служит проводником электрического тока. А кристаллы поваренной соли (NaCl) имеют форму куба.
При производстве алюминия пользуются алюминиево-калиевыми кварцами (K[Al(SO4)2] ⋅ 12H2O), монокристалл которых имеет форму правильного октаэдра.
Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана (FeS). Кристаллы этого химического вещества имеют форму додекаэдра.
В разных химических реакциях применяется сурьменистый сернокислый натрий (Na5(SbO4(SO4)) – вещество, синтезированное учёными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра.
Последний правильный многогранник – икосаэдр передаёт форму кристаллов бора (В). В своё время бор использовался для создания полупроводников первого поколения.
Взять хотя бы поваренную соль, без которой мы не можем обойтись. Известно, что она растворима в воде, служит проводником электрического тока. А кристаллы поваренной соли (NaCl) имеют форму куба.
При производстве алюминия пользуются алюминиево-калиевыми кварцами (K[Al(SO4)2] ⋅ 12H2O), монокристалл которых имеет форму правильного октаэдра.
Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана (FeS). Кристаллы этого химического вещества имеют форму додекаэдра.
В разных химических реакциях применяется сурьменистый сернокислый натрий (Na5(SbO4(SO4)) – вещество, синтезированное учёными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра.
Последний правильный многогранник – икосаэдр передаёт форму кристаллов бора (В). В своё время бор использовался для создания полупроводников первого поколения.
