Муниципальное казённое общеобразовательное учреждение
«Нидымская основная школа»
Эвенкийского муниципального района Красноярского края
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Четырехугольники
Содержание
- 1. Презентация по математике Четырехугольники
- 2. Цель проекта: Исследование и сравнение свойств четырёхугольников.Задачи:
- 3. дельтоид
- 4. Немного историиГеометрия – это предмет для тех
- 5. С геометрическими фигурами имел дело и кожевник,
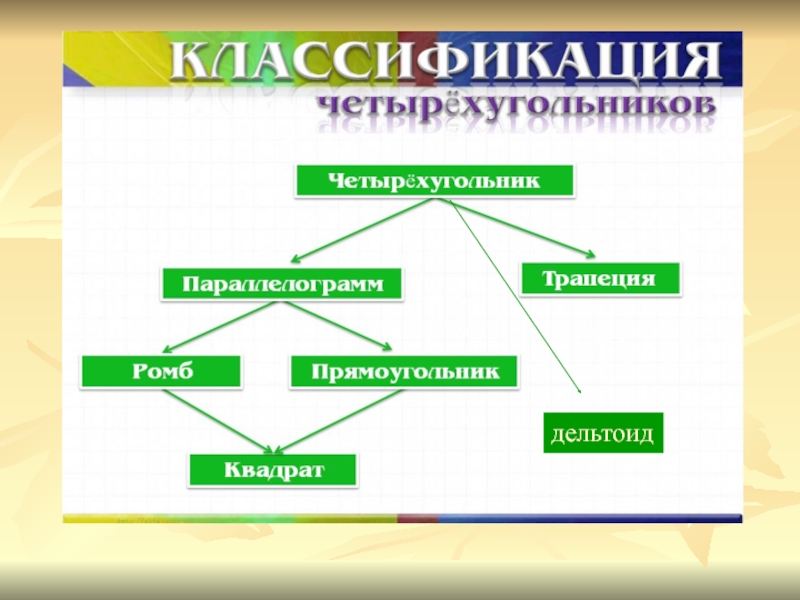
- 6. ЧетырехугольникЧетырехугольником - называется фигура состоящая из четырех точек и четырех последовательно соединяющих их отрезков.
- 7. ПараллелограммПараллелограммом называется четырехугольник, у которого все
- 8. Признаки параллелограмма:Четырёхугольник является параллелограммом, если:две его противоположные
- 9. Параллелограмм в жизни человека
- 10. РОМБРомбом называется параллелограмм, у которого все
- 11. Признаки ромбаПараллелограмм является ромбом, если:две его смежные
- 12. Ромб на службе человека
- 13. ПрямоугольникПрямоугольником называется параллелограмм, у которого все углы
- 14. Признаки прямоугольникаПараллелограмм является прямоугольником, если:один из его углов прямой;его диагонали равны.
- 15. Прямоугольник в жизни
- 16. КвадратКвадратом называется прямоугольник, у которого все стороны
- 17. Признаки квадратаПрямоугольник является квадратом, если:две его смежные
- 18. Квадрат в жизни
- 19. ТрапецияТрапецией называют четырехугольник, у которого две стороны
- 20. Свойства трапеции.средняя линия параллельна основаниям и равна
- 21. Трапеция в жизни
- 22. ДельтоидДельтоид — четырёхугольник, обладающий двумя парами сторон одинаковой
- 23. Свойства дельтоидауглы между сторонами неравной длины равны.диагонали
- 24. Слайд 24
- 25. Слайд 25
- 26. Сказка - вопрос Собрались все четырёхугольники
- 27. Спасибо за внимание !
Цель проекта: Исследование и сравнение свойств четырёхугольников.Задачи: изучить свойства сторон четырёхугольников; Изучить свойства углов четырёхугольников; Рассмотреть особые свойства четырёхугольников.Методы: систематический сбор информации.Объект исследования: геометрические фигуры - четырёхугольники.Актуальность работы
Слайд 1ЧЕТЫРЕХУГОЛЬНИКИ
Выполнила работу: ученица 8 класса
Маймага Сардана.
Руководитель: Габдулхаева Татьяна Николаевна –
учитель
математики.
Слайд 2
Цель проекта: Исследование и сравнение свойств четырёхугольников.
Задачи: изучить свойства сторон четырёхугольников;
Изучить свойства углов четырёхугольников;
Рассмотреть особые свойства четырёхугольников.
Методы: систематический сбор информации.
Объект исследования: геометрические фигуры - четырёхугольники.
Актуальность работы состоит в том, что изучая геометрию многие не замечают сходства и различия свойств этих фигур.
Гипотеза исследования: если в систему работы по математике целенаправленно и систематично включать задания, выполнение которых предполагает проведение учебных исследований, то это позволит повысить степень обученности учащихся и развить их творческую самостоятельность, будет способствовать развитию у учащихся мыслительных процессов, в том числе творческого мышления.
Рассмотреть особые свойства четырёхугольников.
Методы: систематический сбор информации.
Объект исследования: геометрические фигуры - четырёхугольники.
Актуальность работы состоит в том, что изучая геометрию многие не замечают сходства и различия свойств этих фигур.
Гипотеза исследования: если в систему работы по математике целенаправленно и систематично включать задания, выполнение которых предполагает проведение учебных исследований, то это позволит повысить степень обученности учащихся и развить их творческую самостоятельность, будет способствовать развитию у учащихся мыслительных процессов, в том числе творческого мышления.
Слайд 4Немного истории
Геометрия – это предмет для тех , кому нравится фантазировать,
рисовать, кто умеет наблюдать, замечать и делать выводы. Это наверное самая древняя наука и возникла она из практических потребностей людей.
Слайд 5С геометрическими фигурами имел дело и кожевник, резавший шкуру, и кузнец,
ковавший железные изделия, и портной , и строитель храмов, дворцов, пирамид.
Слово «геометрия» греческое, в переводе на русский язык означает «землемерие»
Сегодня мы познакомимся с четырёхугольниками и их свойствами.
Слово «геометрия» греческое, в переводе на русский язык означает «землемерие»
Сегодня мы познакомимся с четырёхугольниками и их свойствами.
Слайд 6Четырехугольник
Четырехугольником - называется фигура состоящая из четырех точек и четырех последовательно
соединяющих их отрезков.
Слайд 7Параллелограмм
Параллелограммом называется четырехугольник, у которого все стороны попарно параллельны.
Свойства параллелограмма:
противолежащие стороны равны;:
противоположные углы равны;
диагонали точкой пересечения делятся пополам;
сумма углов, прилежащих к одной стороне, равна 180;
сумма квадратов диагоналей равна сумме квадратов всех сторон.
противолежащие стороны равны;:
противоположные углы равны;
диагонали точкой пересечения делятся пополам;
сумма углов, прилежащих к одной стороне, равна 180;
сумма квадратов диагоналей равна сумме квадратов всех сторон.
Слайд 8Признаки параллелограмма:
Четырёхугольник является параллелограммом, если:
две его противоположные стороны равны и параллельны;
противоположные
стороны попарно равны;
противоположные углы равны;
диагонали точкой пересечения делятся пополам.
противоположные углы равны;
диагонали точкой пересечения делятся пополам.
Слайд 10РОМБ
Ромбом называется параллелограмм, у которого все стороны равны.
Свойства ромба:
противоположные стороны равны;
противоположные углы равны;
диагонали точкой пересечения делятся пополам;
сумма углов, прилежащих к одной стороне, равна 180;
сумма квадратов диагоналей равна сумме квадратов всех сторон;
диагонали перпендикулярны;
диагонали являются биссектрисами углов.
противоположные стороны равны;
противоположные углы равны;
диагонали точкой пересечения делятся пополам;
сумма углов, прилежащих к одной стороне, равна 180;
сумма квадратов диагоналей равна сумме квадратов всех сторон;
диагонали перпендикулярны;
диагонали являются биссектрисами углов.
Слайд 11Признаки ромба
Параллелограмм является ромбом, если:
две его смежные стороны равны;
его диагонали перпендикулярны;
одна
из диагоналей является биссектрисой его угла.
Слайд 13Прямоугольник
Прямоугольником называется параллелограмм, у которого все углы прямые.
Свойства прямоугольника:
противолежащие стороны равны;:
противоположные углы равны;
диагонали точкой пересечения делятся пополам;
сумма углов, прилежащих к одной стороне, равна 180;
сумма квадратов диагоналей равна сумме квадратов всех сторон;
диагонали равны.
противолежащие стороны равны;:
противоположные углы равны;
диагонали точкой пересечения делятся пополам;
сумма углов, прилежащих к одной стороне, равна 180;
сумма квадратов диагоналей равна сумме квадратов всех сторон;
диагонали равны.
Слайд 14Признаки прямоугольника
Параллелограмм является прямоугольником, если:
один из его углов прямой;
его диагонали равны.
Слайд 16Квадрат
Квадратом называется прямоугольник, у которого все стороны равны
Свойства квадрата:
все углы квадрата прямые;
диагонали квадрата равны;
диагонали взаимно перпендикулярны;
диагонали точкой пересечения делятся пополам;
диагонали делят углы квадрата пополам.
все углы квадрата прямые;
диагонали квадрата равны;
диагонали взаимно перпендикулярны;
диагонали точкой пересечения делятся пополам;
диагонали делят углы квадрата пополам.
Слайд 17Признаки квадрата
Прямоугольник является квадратом, если:
две его смежные стороны равны;
его диагонали перпендикулярны;
одна
из диагоналей является биссектрисой его угла.
Слайд 19Трапеция
Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие
стороны не параллельны.
Параллельные стороны трапеции называются
ёё основаниями, а непараллельные – боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией.
Трапеция называется равнобедренной (или равнобокой),если её боковые стороны равны.
Трапеция, один из углов которой прямой, называется прямоугольной.
Слайд 20Свойства трапеции.
средняя линия параллельна основаниям и равна их полусумме;
если трапеция равнобокая,
то её диагонали равны и углы при основании равны;
если трапеция равнобокая, то около неё можно описать окружность;
если сумма оснований равна сумме боковых сторон, то в неё можно вписать окружность.
Признаки трапеции.
четырёхугольник является трапецией, если его параллельные стороны не равны.
если трапеция равнобокая, то около неё можно описать окружность;
если сумма оснований равна сумме боковых сторон, то в неё можно вписать окружность.
Признаки трапеции.
четырёхугольник является трапецией, если его параллельные стороны не равны.
Слайд 22Дельтоид
Дельтоид — четырёхугольник, обладающий двумя парами сторон одинаковой длины. В отличие от
параллелограмма, равными являются не противоположные, а две пары смежных сторон. Дельтоид имеет форму, похожую на воздушного змея.
Слайд 23Свойства дельтоида
углы между сторонами неравной длины равны.
диагонали дельтоида (или их продолжения)
пересекаются под прямым углом.
в любой выпуклый дельтоид можно вписать окружность, кроме этого, если дельтоид не является ромбом, то существует ещё одна окружность, касающаяся продолжений всех четырёх сторон. Для невыпуклого дельтоида можно построить окружность, касающуюся двух бо́льших сторон и продолжений двух меньших сторон и окружность, касающуюся двух меньших сторон и продолжений двух больших сторон.
в любой выпуклый дельтоид можно вписать окружность, кроме этого, если дельтоид не является ромбом, то существует ещё одна окружность, касающаяся продолжений всех четырёх сторон. Для невыпуклого дельтоида можно построить окружность, касающуюся двух бо́льших сторон и продолжений двух меньших сторон и окружность, касающуюся двух меньших сторон и продолжений двух больших сторон.
Слайд 26Сказка - вопрос
Собрались все четырёхугольники на лесной поляне и
стали обсуждать вопрос о выборе короля. Долго спорили и никак не могли прийти к единому мнению. И вот один старый параллелограмм сказал: «Давайте отправимся все в царство четырёхугольников. Кто первым дойдёт, тот и будет королём». Все согласились. Рано утром отправились все в путешествие. На пути путешественников повстречалась река, которая сказала: «Переплывут меня только те, у кого диагонали пересекаются и точкой пересечения делятся пополам». Часть четырёхугольников осталась на берегу, остальные благополучно переплыли и отправились дальше. Затем на пути им повстречалась высокая гора, которая сказала, что даст пройти только тем, у кого диагонали равны. Несколько путешественников остались у горы, остальные продолжили путь. Дошли до большого обрыва, где был узкий мост. Мост сказал, что пропустит тех, у кого диагонали пересекаются под прямым углом. По мосту прошёл один четырёхугольник, который первым добрался до царства и был провозглашён королём.
1.Кто стал королём? 2. Кто был основным соперником? 3. Кто первым выбыл из соревнования?
1.Кто стал королём? 2. Кто был основным соперником? 3. Кто первым выбыл из соревнования?