- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике 10-11 класс на тему Построение перпендикулярных прямой и плоскости
Содержание
- 1. Презентация по математике 10-11 класс на тему Построение перпендикулярных прямой и плоскости
- 2. ЗАДАЧА 1. Через данную точку М провести
- 3. I. Рассмотрим случай, когда М ∉ а
- 4. Далее, через прямую а проведем любую плоскость
- 5. Предположим, что через точку М можно провести
- 6. II. Случай, когда М ∈ а,рассмотрите самостоятельно. Его иллюстрация дана на рис 3.Рис.3
- 7. ЗАДАЧА 2. Через данную точку
- 8. I. M∈ α (рис. 4, а). Шаги
- 9. В самом деле, прямая с проходит (по
- 10. Через каждую точку пространства
- 11. Потоскуев Е. В. Геометрия 10 кл.: Учеб.
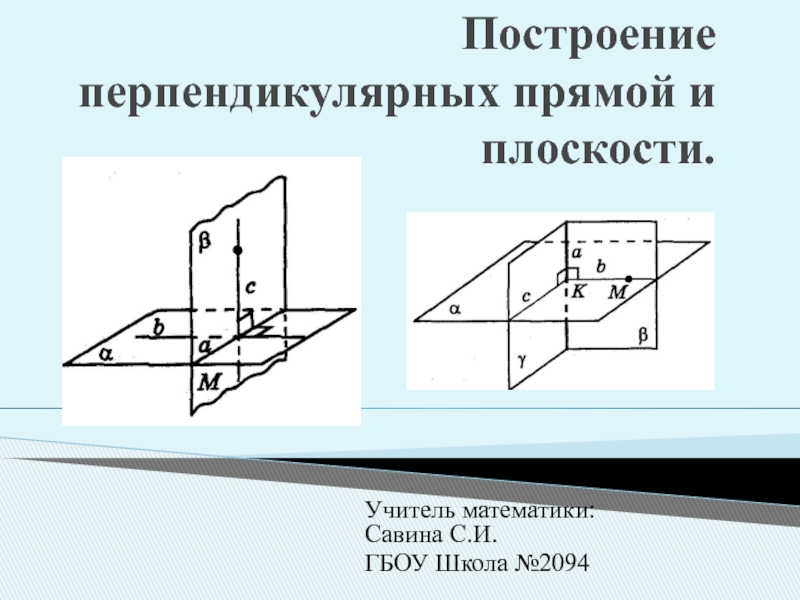
Слайд 1Построение перпендикулярных прямой и плоскости.
Учитель математики: Савина С.И.
ГБОУ Школа №2094
Слайд 2ЗАДАЧА 1. Через данную точку М провести
плоскость ɑ, перпендикулярную данной
прямой а.
В решении возможны два случая:
1)точка М не принадлежит данной прямой а;
2) точка М принадлежит данной прямой а.
Решим две задачи.
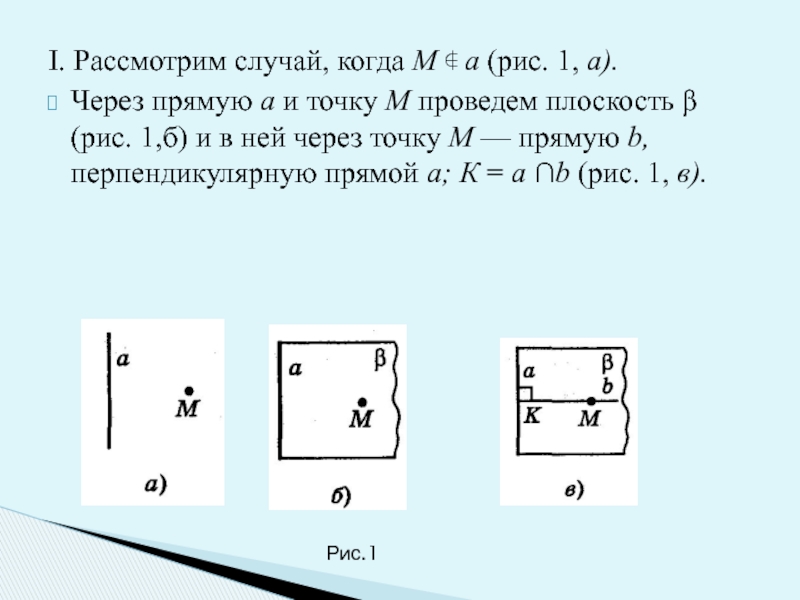
Слайд 3I. Рассмотрим случай, когда М ∉ а (рис. 1, а).
Через прямую
Рис.1
Слайд 4Далее, через прямую а проведем любую плоскость γ (рис. 1, г),
Теперь через прямые b и с проведем плоскость а
(рис. 1, е), которая по признаку перпендикулярности прямой и плоскости перпендикулярна прямой а
(с ⊂ α, b⊂ α, с∩ b = К, a ⊥ с, a ⊥b).
Таким образом, α — искомая плоскость.
Рис.1
Слайд 5Предположим, что через точку М можно провести другую плоскость, например α1
Докажем, что α— единственная плоскость, удовлетворяющая условию задачи.
Рис.2
Слайд 7 ЗАДАЧА 2. Через данную точку М провести прямую а,
В решении возможны два случая:
1)точка М принадлежит плоскости α;
2) точка М не принадлежит плоскости α.
Слайд 8I. M∈ α (рис. 4, а).
Шаги построения:
1) в плоскости α
2) через точку М проводим плоскость β, перпендикулярную прямой b (задача 1), при этом β пересекает плоскость α по прямой а, перпендикулярной прямой b (рис. 4, в);
3) в плоскости β проводим через точку М прямую с перпендикулярно прямой а (рис. 4, г).
Прямая с — искомая.
Рис.4
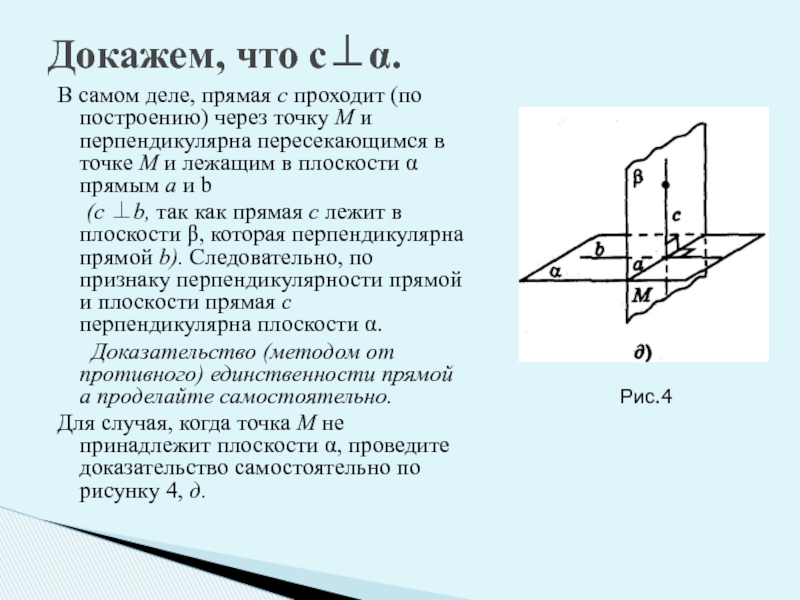
Слайд 9В самом деле, прямая с проходит (по построению) через точку М
(с ⊥b, так как прямая с лежит в плоскости β, которая перпендикулярна прямой b). Следовательно, по признаку перпендикулярности прямой и плоскости прямая с перпендикулярна плоскости α.
Доказательство (методом от противного) единственности прямой а проделайте самостоятельно.
Для случая, когда точка М не принадлежит плоскости α, проведите доказательство самостоятельно по рисунку 4, д.
Докажем, что с⊥α.
Рис.4
Слайд 10 Через каждую точку пространства проходит единственная плоскость, перпендикулярная
В дальнейшем мы, естественно, назовем не имеющие общих точек плоскости параллельными (рис. 5).
Через каждую точку пространства проходит единственная прямая, перпендикулярная данной плоскости, следовательно, две различные прямые, перпендикулярные одной и той же плоскости, не могут пересекаться, такие прямые параллельны (рис.6).
Обобщая вышесказанное, отметим, что:
Рис.5
Рис.6
Слайд 11Потоскуев Е. В.
Геометрия 10 кл.: Учеб. Для общеобразоват. Учреждений с
Используемая литература.