- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрииТеорема Фалеса
Содержание
- 1. Презентация по геометрииТеорема Фалеса
- 2. “Невежество – тяжкое бремя” Фалес Фалес (Thales -
- 3. ЦелиИзучить теорему Фалеса;Научиться делить отрезок на n
- 4. Содержание презентацииТеорема ФалесаЗадача (деление отрезка на Задача
- 5. Теорема Фалеса Если на одной из двух прямых
- 6. Задача (деление отрезка на n равных частей)При
- 7. Средняя линия треугольникаСредней линией треугольника называется отрезок,
- 8. Признак средней линииЕсли отрезок параллелен стороне треугольника,
- 9. Свойства средней линии Дано: ABC – треугольник, ОЄBC,
- 10. Задачид/зСодержание
- 11. Задача №2Докажите, что середины сторон произвольного четырехугольника ABCD являются вершинами параллелограмма.Подсказка 1Подсказка 2РешениеСборник задач
- 12. Подсказка 1 (задача №2)Проведите диагональ AC четырехугольника ABCD.Условие задачи
- 13. Подсказка 2 (задача №2)Найдите средние линии треугольников и примените свойства средней линии треугольникаУсловие задачи
- 14. Решение задачи №2 Дано: ABCD – четырехугольник,
- 15. Задача №4Точки O и F – середины
- 16. Подсказка 1 (задача №4)OF – средняя линия треугольника ABC. Примените свойство средней линии треугольника.Условие задачи
- 17. Решение задачи №4 Дано: ∆ ABC,
- 18. Ответ задачи №4Периметр треугольника ABC равен 14 см.Сборник задач
- 19. Задача №5В равнобедренном треугольнике ABC точки T
- 20. Подсказка 1 (задача №5)Найдите длину основания AC треугольника ABC.Условие задачи
- 21. Подсказка 2 (задача №5)Примените свойство средней линии треугольникаУсловие задачи
- 22. Решение задачи №5Решение. PABC =AB+BC+AC; BC=AB (по
- 23. Ответ задачи №5TO = 4 смСборник задач
- 24. Задача №6В параллелограмме ABCD точки K и
- 25. Подсказка 1 (задача №6)Рассмотрите ∆ABC и ∆ACD.Условие задачи
- 26. Подсказка 2 (задача №6)OK – средняя линия
- 27. Решение задачи №6Решение.OK = OF + 2
- 28. Ответ задачи №6Периметр параллелограмма ABCD равен 64 см.Сборник задач
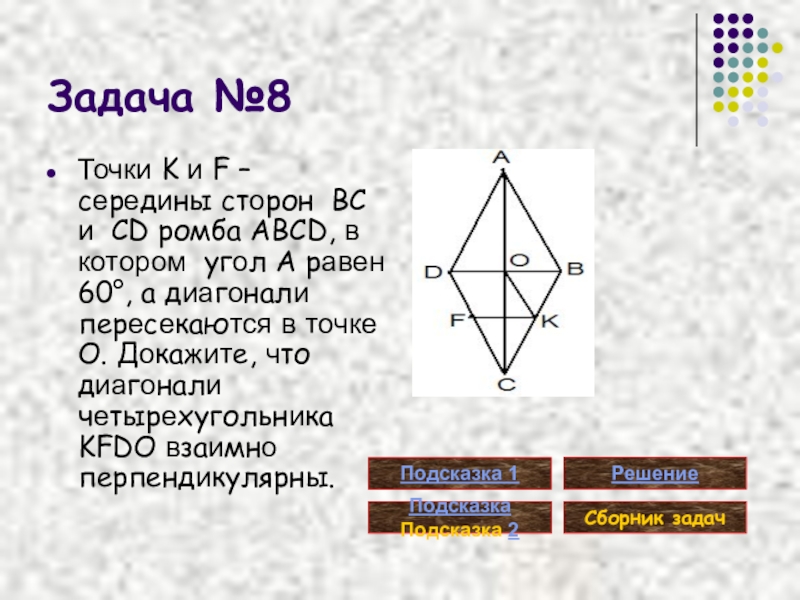
- 29. Задача №8Точки K и F – середины
- 30. Подсказка 1 (задача №8)Докажите, что ∆BCD равносторонний.Умова задачыУсловие задачи
- 31. Подсказка 2 (задача №8)Примените свойства средних линий
- 32. Решение задачи №8 РешениеC =A (противолежащие углы
- 33. Задача №9ABCD – ромб, диагонали которого пересекаются
- 34. Подсказка 1 (задача №9)Докажите, что треугольник ABC - равностороннийУсловие задачи
- 35. Подсказка 2 (задача №9)Примените свойства средних линий треугольника ABC.Условие задачи
- 36. Решение задачи №9Решение.BCD=120°, значит BAD=120° (противоположные углы)
- 37. Ответ задачи №9 Периметр четырехугольника ATFO равен 16 см.Сборник задач
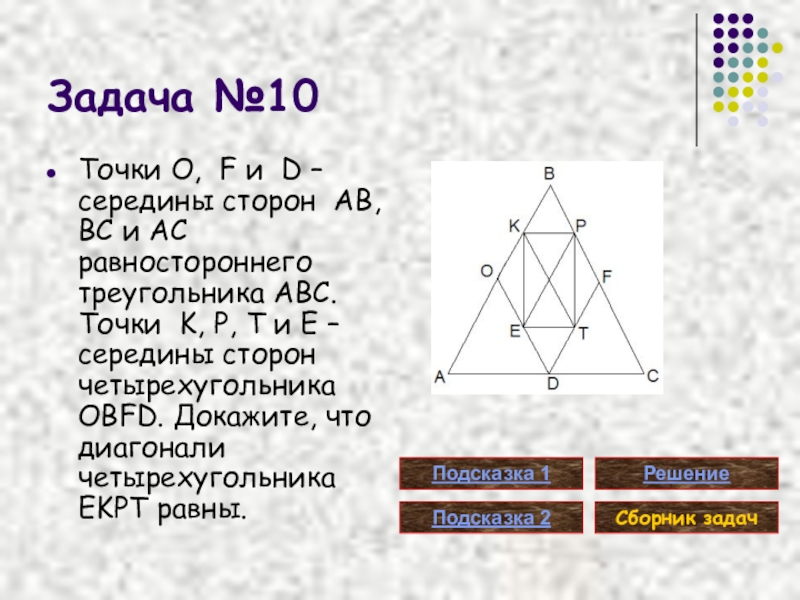
- 38. Задача №10Точки O, F и D –
- 39. Подсказка 1 (задача №10)Чтобы доказать, что KT=PE, надо доказать, что EKPT – прямоугольник.Условие задачи
- 40. Подсказка 2 (задача №10)Докажите, что OBFD –
- 41. Решение задачи №10 Решение.OD и DF – средние
- 42. Задача №11Отрезки CF и BK – высоты
- 43. Подсказка 1 (задача №11)Грани правильного тетраэдра являются равносторонними треугольниками.Условие задачи
- 44. Подсказка 2 (задача №11)Высота равностороннего треугольника является
- 45. Решение задачи №11 Дано: SABC – правильный тетраэдр,
- 46. Ответ задачи №11Длина ломаной ASCB равна 12,6 см.Сборник задач
- 47. Задача №13Отрезок AB – диаметр окружности, С
- 48. Подсказка 1 (задача №13)Докажите, что ACB=90°. Условие задачи
- 49. Решение задачи №13 Решение.l - серединный перпендикуляр к
- 50. Дано: ∆ABC, AB – диаметр,
- 51. Задание на дом§5;№1, №7Рефлексия
- 52. Рефлексия
- 53. Рефлексия
- 54. Рефлексия
- 55. Рефлексия
- 56. Успехов Вам в учебе!Содержание
Слайд 1Теорема Фалеса.
Средняя линия треугольника
9 класс
Учитель математики
ГБОУ СОШ 377
Судиловская Ирина Владимировна
Слайд 2“Невежество – тяжкое бремя” Фалес
Фалес (Thales - жил около 625-547 до
Слайд 3Цели
Изучить теорему Фалеса;
Научиться делить отрезок на n равных частей;
Усвоить понятие средней
Изучить свойства и признак средней линии треугольника;
Научиться применять изученный материал при решении задач
Слайд 4Содержание презентации
Теорема Фалеса
Задача (деление отрезка на Задача (деление отрезка на nЗадача
Средняя линия треугольника
Признак средней линии
Свойства средней линии
Задачи
Рефлексия
Выход
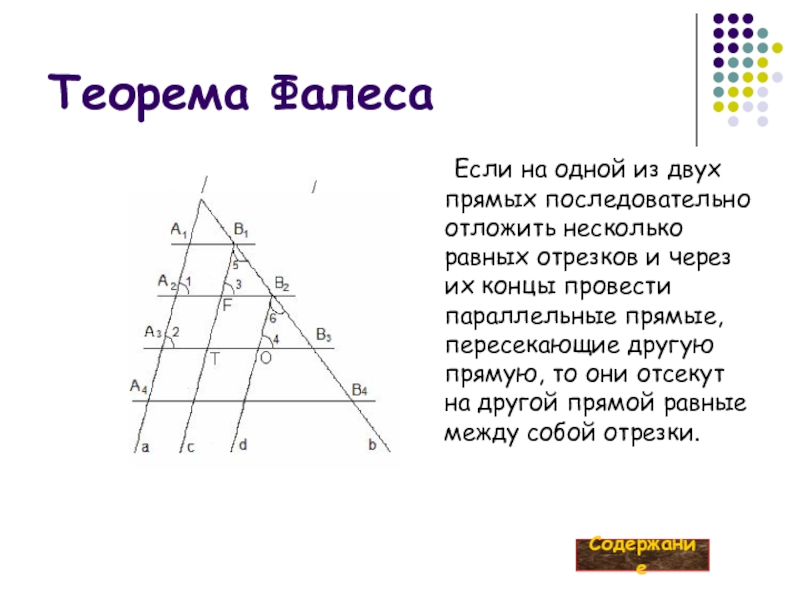
Слайд 5Теорема Фалеса
Если на одной из двух прямых последовательно отложить несколько равных
Содержание
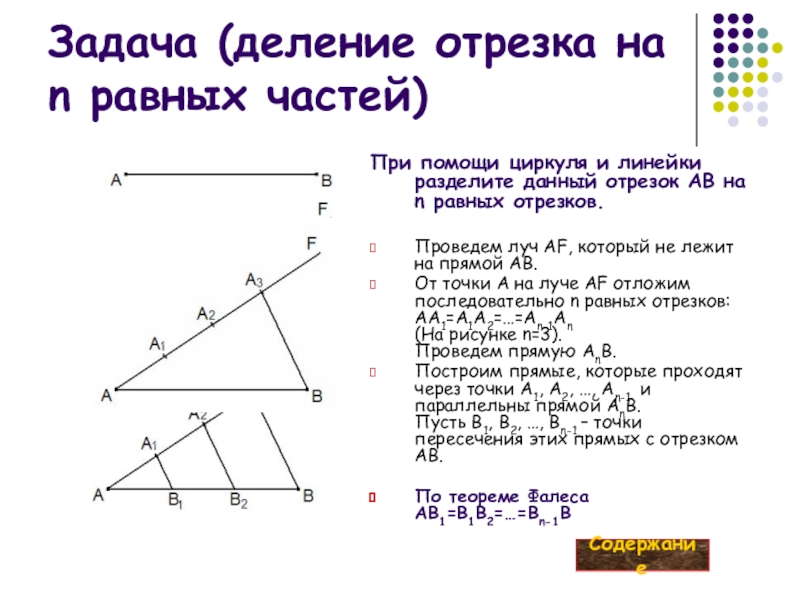
Слайд 6Задача (деление отрезка на n равных частей)
При помощи циркуля и линейки
Проведем луч AF, который не лежит на прямой AB.
От точки A на луче AF отложим последовательно n равных отрезков: AA1=A1A2=…=An-1An (На рисунке n=3). Проведем прямую AnB.
Построим прямые, которые проходят через точки A1, A2, …, An-1 и параллельны прямой AnВ. Пусть B1, B2, …, Bn-1 – точки пересечения этих прямых с отрезком AB.
По теореме Фалеса AB1=B1B2=…=Bn-1B
Содержание
Слайд 7Средняя линия треугольника
Средней линией треугольника называется отрезок, который соединяет середины двух
Любой треугольник имеет три средних линии.
Содержание
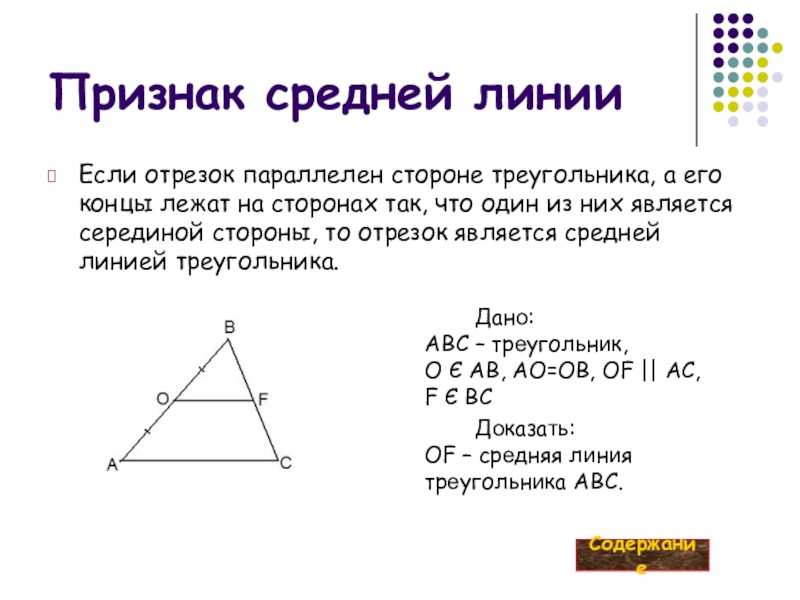
Слайд 8Признак средней линии
Если отрезок параллелен стороне треугольника, а его концы лежат
Дано:
ABC – треугольник,
О Є AB, AO=OB, OF || AC,
F Є BC
Доказать:
OF – средняя линия треугольника ABC.
Содержание
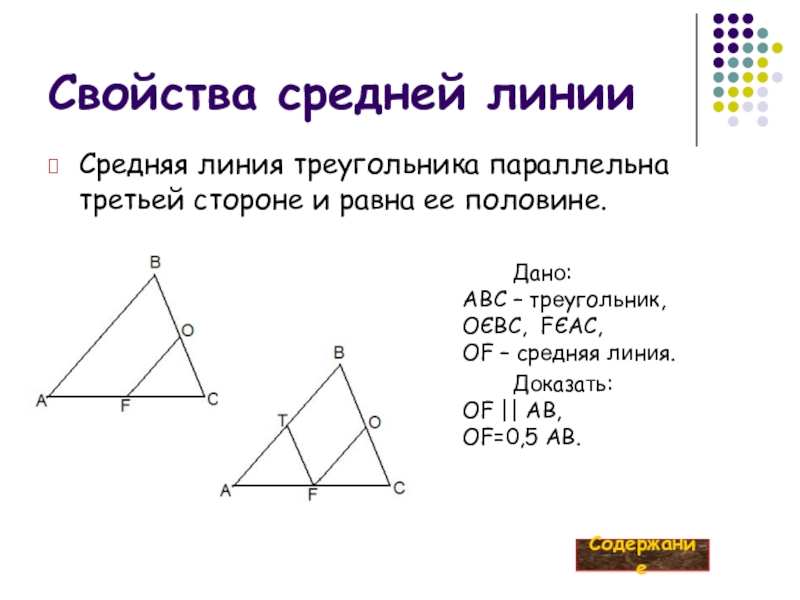
Слайд 9Свойства средней линии
Дано:
ABC – треугольник,
ОЄBC, FЄAC,
OF – средняя линия.
Доказать:
OF || AB,
OF=0,5
Средняя линия треугольника параллельна третьей стороне и равна ее половине.
Содержание
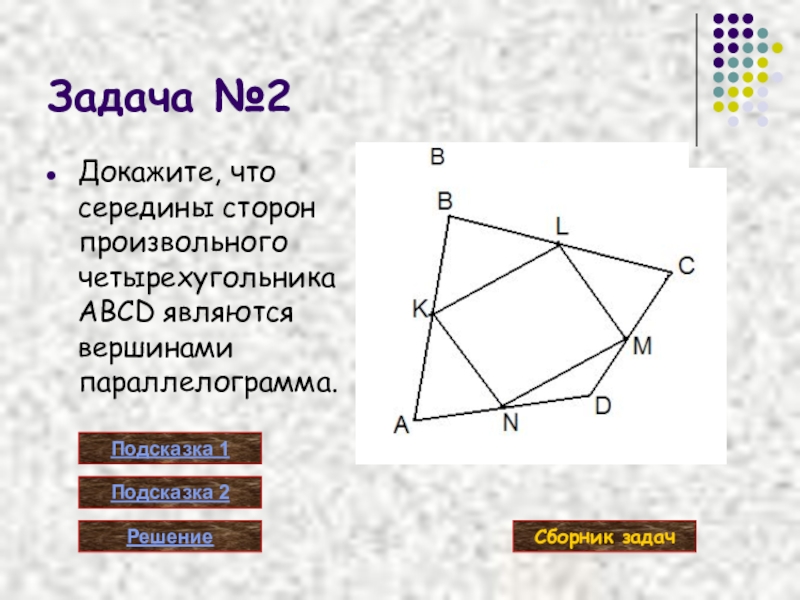
Слайд 11Задача №2
Докажите, что середины сторон произвольного четырехугольника ABCD являются вершинами параллелограмма.
Подсказка
Подсказка 2
Решение
Сборник задач
Слайд 13Подсказка 2 (задача №2)
Найдите средние линии треугольников и примените свойства средней
Условие задачи
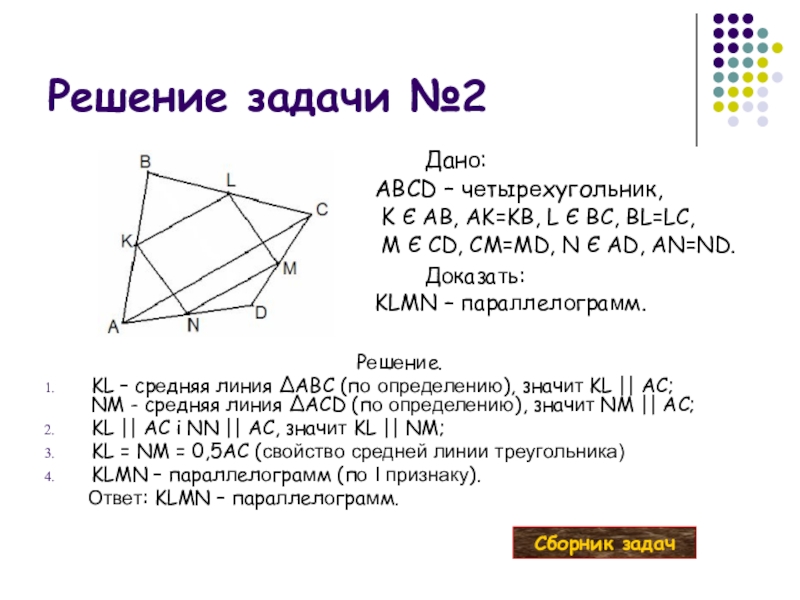
Слайд 14Решение задачи №2
Дано:
ABCD – четырехугольник,
K Є AB, AK=KB, L Є
Доказать: KLMN – параллелограмм.
Решение.
KL – средняя линия ∆ABC (по определению), значит KL || AC;
NM - средняя линия ∆ACD (по определению), значит NM || AC;
KL || AC і NN || AC, значит KL || NM;
KL = NM = 0,5AC (свойство средней линии треугольника)
KLMN – параллелограмм (по І признаку).
Ответ: KLMN – параллелограмм.
Сборник задач
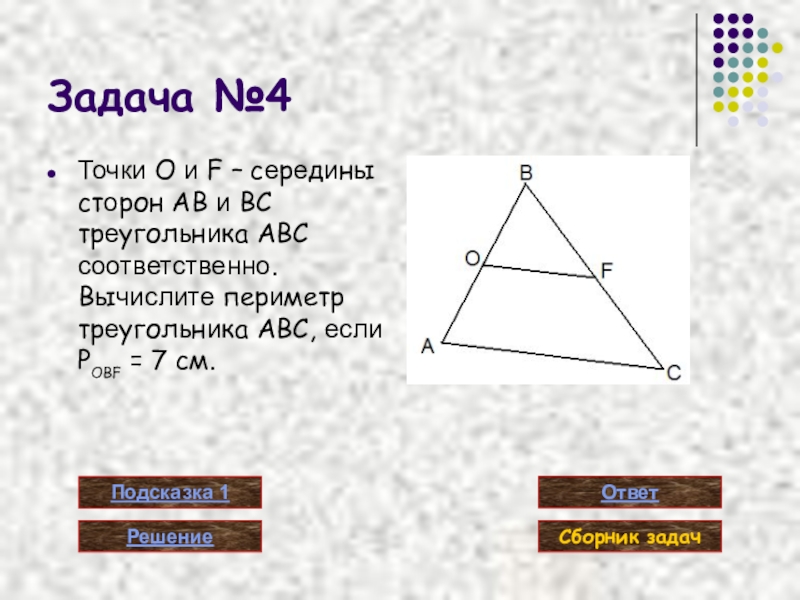
Слайд 15Задача №4
Точки O и F – середины сторон AB и BC
Подсказка 1
Решение
Ответ
Сборник задач
Слайд 16Подсказка 1 (задача №4)
OF – средняя линия треугольника ABC.
Примените свойство средней
Условие задачи
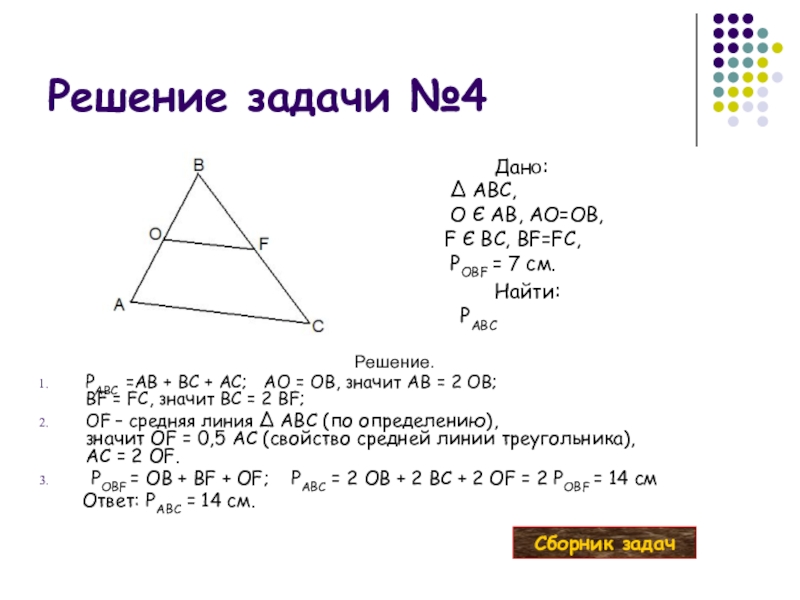
Слайд 17Решение задачи №4
Дано:
∆ ABC,
O Є AB, AO=OB,
F Є
Найти: PABC
Решение.
PABC =AB + BC + AC; AO = OB, значит AB = 2 OB;
BF = FC, значит BC = 2 BF;
OF – средняя линия ∆ ABC (по определению),
значит OF = 0,5 AC (свойство средней линии треугольника),
AC = 2 OF.
POBF = OB + BF + OF; PABC = 2 OB + 2 BC + 2 OF = 2 POBF = 14 см
Ответ: PABC = 14 см.
Сборник задач
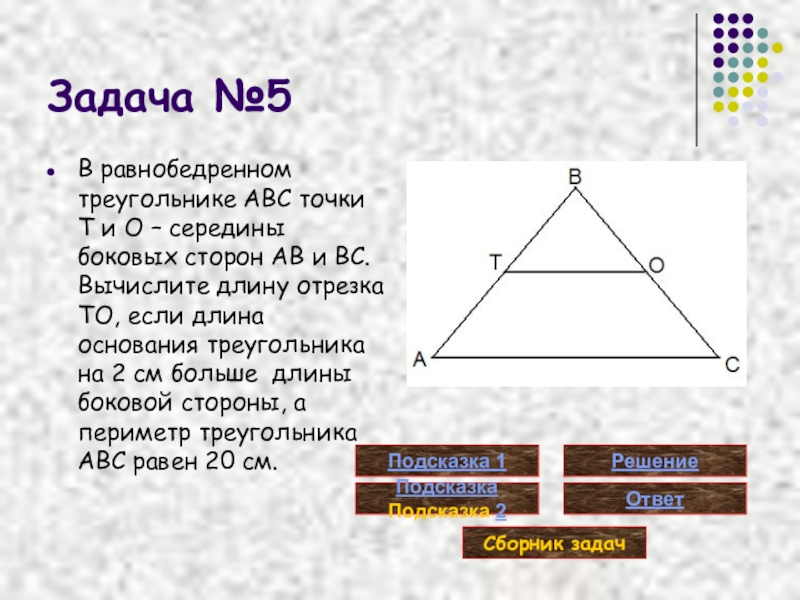
Слайд 19Задача №5
В равнобедренном треугольнике ABC точки T и O – середины
Сборник задач
Подсказка 1
Решение
Подсказка Подсказка 2
Ответ
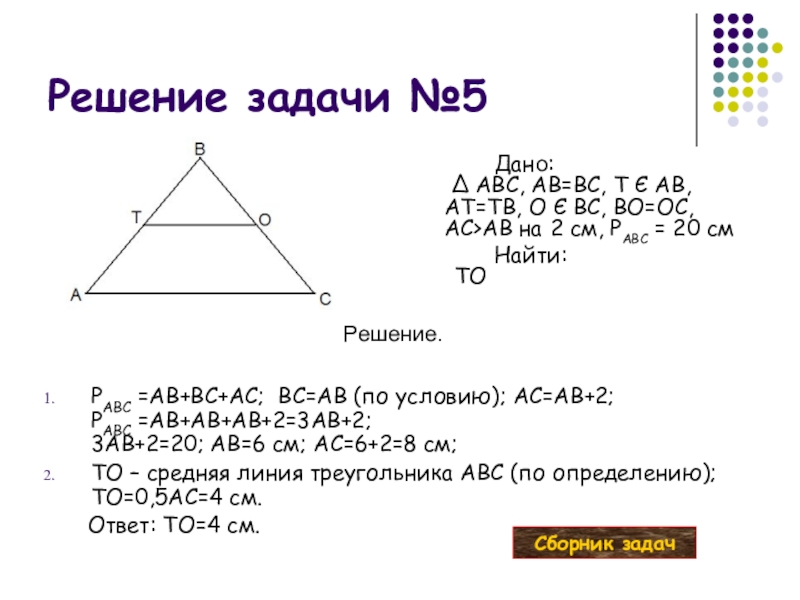
Слайд 22Решение задачи №5
Решение.
PABC =AB+BC+AC; BC=AB (по условию); AC=AB+2;
PABC =AB+AB+AB+2=3AB+2;
3AB+2=20; AB=6
TO – средняя линия треугольника ABC (по определению); TO=0,5AC=4 см.
Ответ: TO=4 см.
Дано:
∆ ABC, AB=BC, T Є AB, AT=TB, O Є BC, BO=OC,
AC>AB на 2 см, PABC = 20 см
Найти:
TO
Сборник задач
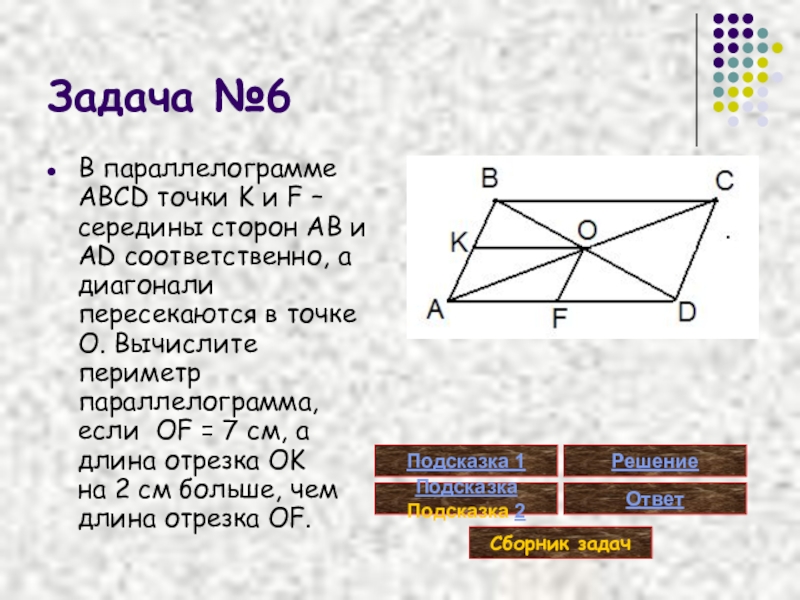
Слайд 24Задача №6
В параллелограмме ABCD точки K и F – середины сторон
Сборник задач
Подсказка 1
Подсказка Подсказка 2
Решение
Ответ
Слайд 26Подсказка 2 (задача №6)
OK – средняя линия ∆ABC;
OF – средняя
Примените свойство средней линии треугольника
Условие задачи
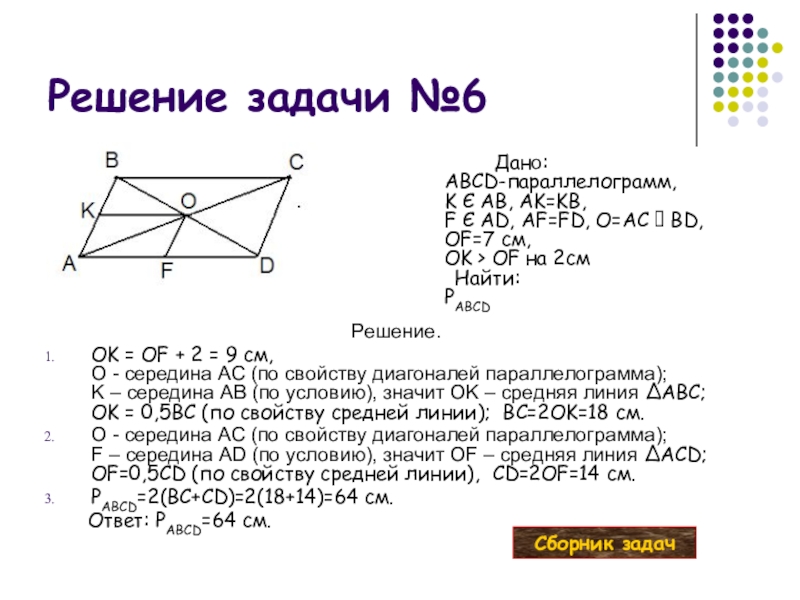
Слайд 27Решение задачи №6
Решение.
OK = OF + 2 = 9 см,
O
O - середина AC (по свойству диагоналей параллелограмма); F – середина AD (по условию), значит OF – средняя линия ∆ACD; OF=0,5CD (по свойству средней линии), CD=2OF=14 см.
PABCD=2(BC+CD)=2(18+14)=64 см.
Ответ: PABCD=64 см.
Дано:
ABCD-параллелограмм,
K Є AB, AK=KB,
F Є AD, AF=FD, O=AC BD,
OF=7 см,
OK > OF на 2см
Найти:
PABCD
Сборник задач
Слайд 29Задача №8
Точки K и F – середины сторон BC и CD
Сборник задач
Подсказка 1
Подсказка Подсказка 2
Решение
Слайд 31Подсказка 2 (задача №8)
Примените свойства средних линий треугольника.
Докажите, что KFDO –
Докажите, что KFDO – ромб;
Условие задачи
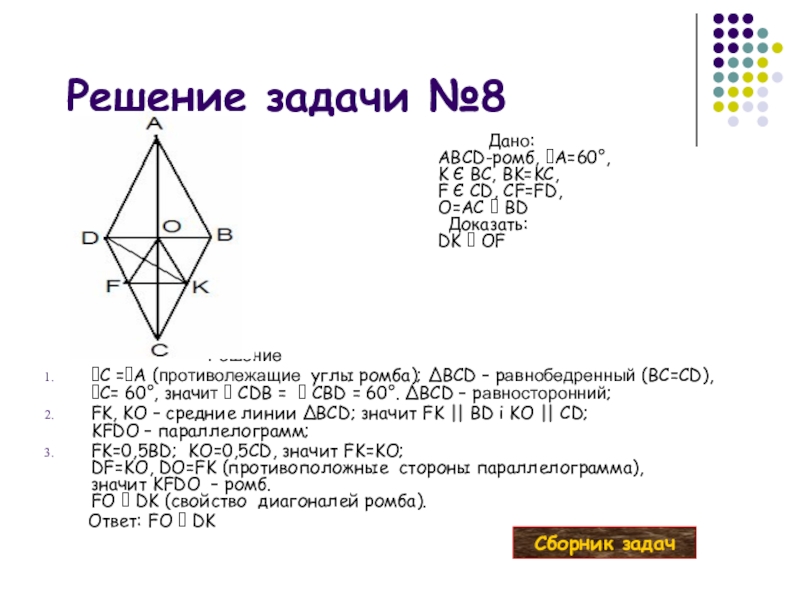
Слайд 32 Решение задачи №8
Решение
C =A (противолежащие углы ромба); ∆BCD – равнобедренный
FK, KO – средние линии ∆BCD; значит FK || BD i KO || CD; KFDO – параллелограмм;
FK=0,5BD; KO=0,5CD, значит FK=KO; DF=KO, DO=FK (противоположные стороны параллелограмма), значит KFDO – ромб. FO DK (свойство диагоналей ромба).
Ответ: FO DK
Дано:
ABCD-ромб, A=60°,
K Є BС, BK=KC,
F Є CD, CF=FD,
O=AC BD
Доказать:
DK OF
Сборник задач
Слайд 33Задача №9
ABCD – ромб, диагонали которого пересекаются в точке O и
Сборник задач
Подсказка 1
Подсказка Подсказка 2
Решение
Ответ
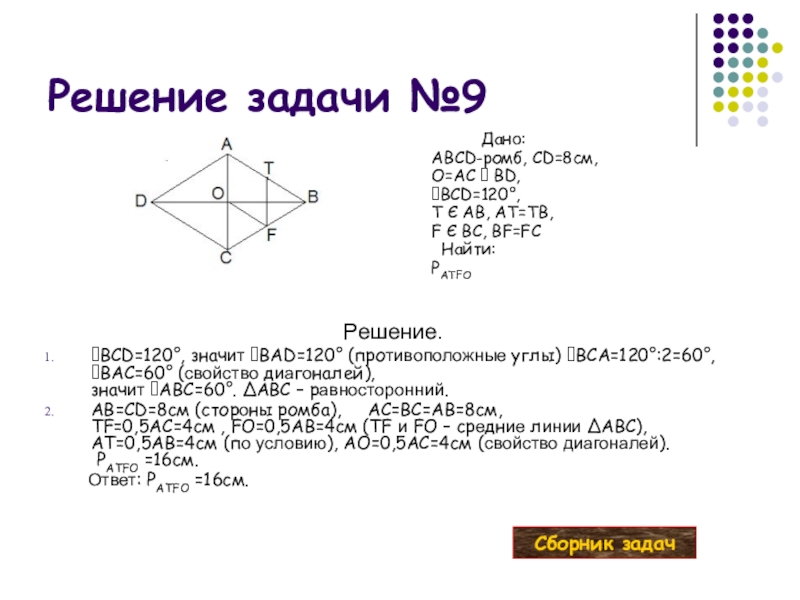
Слайд 36Решение задачи №9
Решение.
BCD=120°, значит BAD=120° (противоположные углы) BCA=120°:2=60°, BAC=60° (свойство диагоналей),
значит
AB=CD=8см (стороны ромба), AC=BC=AB=8см, TF=0,5AC=4см , FO=0,5AB=4см (TF и FO – средние линии ∆ABC), AT=0,5AB=4см (по условию), AO=0,5AC=4см (свойство диагоналей). PATFO =16см.
Ответ: PATFO =16см.
Дано:
ABCD-ромб, CD=8см,
O=AC BD,
BCD=120°,
T Є AB, AT=TB,
F Є BC, BF=FC
Найти:
PATFO
Сборник задач
Слайд 38Задача №10
Точки O, F и D – середины сторон AB, BC
Сборник задач
Подсказка 1
Подсказка 2
Решение
Слайд 39Подсказка 1 (задача №10)
Чтобы доказать, что KT=PE, надо доказать, что EKPT
Условие задачи
Слайд 40Подсказка 2 (задача №10)
Докажите, что OBFD – ромб;
Докажите, что EKPT –
Докажите, что EKPT – прямоугольник.
Условие задачи
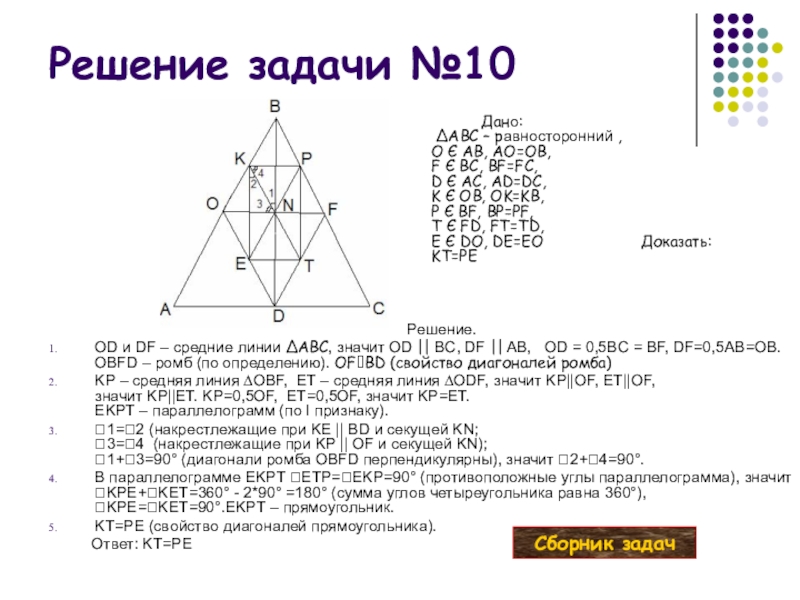
Слайд 41Решение задачи №10
Решение.
OD и DF – средние линии ∆ABC, значит OD
KP – средняя линия ∆OBF, ET – средняя линия ∆ODF, значит KP||OF, ET||OF, значит KP||ET. KP=0,5OF, ET=0,5OF, значит KP=ET. EKPT – параллелограмм (по І признаку).
1=2 (накрестлежащие при KE || BD и секущей KN; 3=4 (накрестлежащие при KP || OF и секущей KN); 1+3=90° (диагонали ромба OBFD перпендикулярны), значит 2+4=90°.
В параллелограмме EKPT ETP=EKP=90° (противоположные углы параллелограмма), значит KPЕ+KET=360° - 2*90° =180° (сумма углов четыреугольника равна 360°), KPE=KET=90°.EKPT – прямоугольник.
KT=PE (свойство диагоналей прямоугольника).
Ответ: KT=PE
Дано:
∆ABC – равносторонний ,
O Є AB, AO=OB,
F Є BC, BF=FC,
D Є AC, AD=DC,
K Є OB, OK=KB,
P Є BF, BP=PF,
T Є FD, FT=TD,
E Є DO, DE=EO Доказать:
KT=PE
Сборник задач
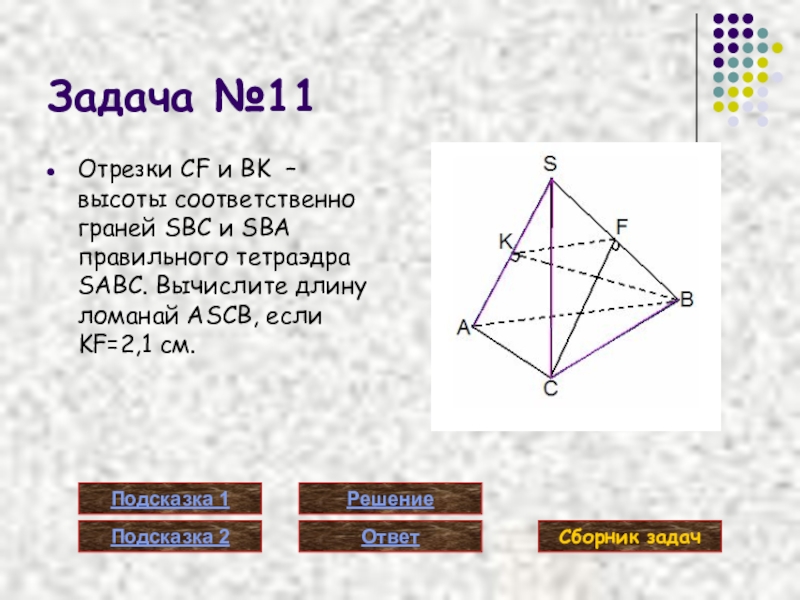
Слайд 42Задача №11
Отрезки CF и BK – высоты соответственно граней SBC и
Ответ
Подсказка 2
Подсказка 1
Решение
Сборник задач
Слайд 43Подсказка 1 (задача №11)
Грани правильного тетраэдра являются равносторонними треугольниками.
Условие задачи
Слайд 44Подсказка 2 (задача №11)
Высота равностороннего треугольника является и его медианой.
Средняя линия
Условие задачи
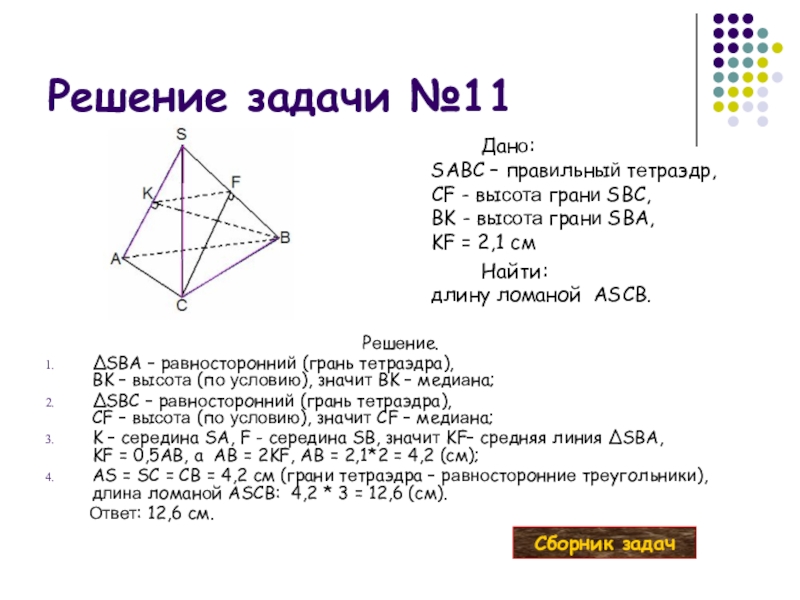
Слайд 45Решение задачи №11
Дано:
SABC – правильный тетраэдр,
CF - высота грани SBC,
BK
Найти: длину ломаной ASCB.
Решение.
∆SBA – равносторонний (грань тетраэдра),
BK – высота (по условию), значит BK – медиана;
∆SBC – равносторонний (грань тетраэдра),
CF – высота (по условию), значит CF – медиана;
K – середина SA, F - середина SB, значит KF– средняя линия ∆SBA,
KF = 0,5AB, а AB = 2KF, AB = 2,1*2 = 4,2 (см);
AS = SC = CB = 4,2 см (грани тетраэдра – равносторонние треугольники), длина ломаной ASCB: 4,2 * 3 = 12,6 (см).
Ответ: 12,6 см.
Сборник задач
Слайд 47Задача №13
Отрезок AB – диаметр окружности, С – произвольная точка на
Сборник задач
Подсказка 1
Решение
Слайд 49Решение задачи №13
Решение.
l - серединный перпендикуляр к AC, значит F Є
ACB=90° (посмотреть доказательство); l AC, BC AC, значит l || BC.
FO – средняя линия ∆ABC (по признаку средней линии)
Ответ: FO – средняя линия ∆ABC.
Дано:
AB- диаметр окружности,
С – точка на окружности,
l – серединный перпендикуляр к AC,
l AB=O,
F Є AC, AF=FC,
Доказать:
FO – средняя линия ∆ABC
Сборник задач
Слайд 50
Дано:
∆ABC, AB – диаметр,
С – точка на окружности
Доказать:
Доказательство.
О – центр окружности;
∆OBC – равнобедренный (OB=OC радиусы),
пусть BOC = x, тогда BCO = (180°- x) : 2= 90° – 0,5x;
∆OAC – равнобедренный (OA=OC радиусы),
AOC = 180°- x (смежный с BOC );
ACO = (180°- (180°- x)) : 2 = 0,5x
ACB = 90°- 0,5x + 0,5x = 90°
Ответ: ACB=90°