часов)
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Взаимное расположение прямых в пространстве
Содержание
- 1. Презентация по геометрии Взаимное расположение прямых в пространстве
- 2. Введение в стереометриюУрок 49,50
- 3. ГеометрияПланиметрияСтереометрия stereos - телесный, твердый, объемный, пространственныйmetreo - измерять
- 4. Стереометрия.Раздел геометрии, в котором изучаются свойства фигур в пространстве.Основные фигуры в пространстве:АТочка.аПрямая.Плоскость.
- 5. Обозначение основных фигур в пространстве:точкапрямаяплоскостьA, B, C, …a, b, c, …илиAВ, BС, CD, …
- 6. Аксиома(от греч. axíõma – принятие положения)исходное положение научной теории, принимаемое без доказательства
- 7. Аксиомы стереометрииI. Какова бы ни была прямая,
- 8. C1. Какова бы ни была плоскость, существуют
- 9. АКСИОМА стереометрии.С2. Если две различные плоскости имеют
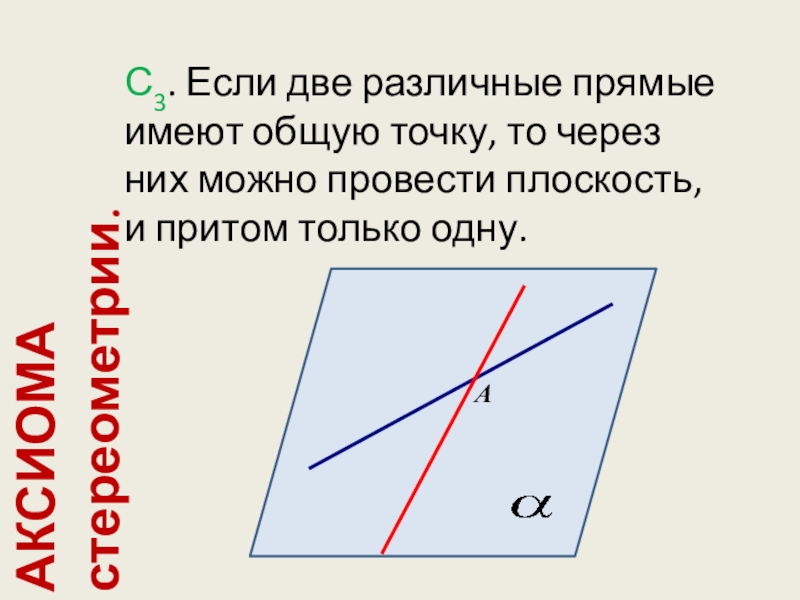
- 10. АКСИОМА стереометрии.С3. Если две различные прямые имеют
- 11. Утверждение, требующее доказательства, на основе известных теорем и аксиом.Теорема
- 12. Теорема 15.1. Через прямую и не лежащую
- 13. Теоремы стереометрии.Теорема 15.2. Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскостиАВ
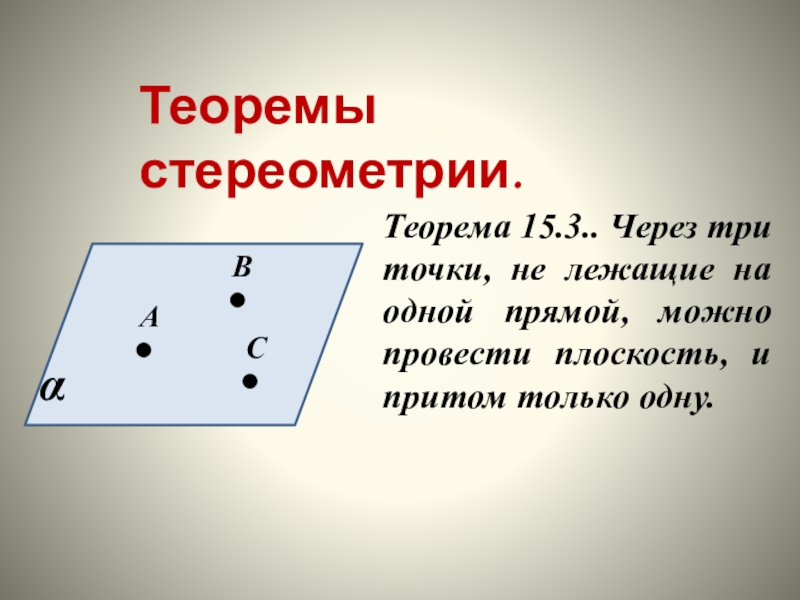
- 14. Теоремы стереометрии.Теорема 15.3.. Через три точки, не
- 15. Теорема 15.4. Плоскость разбивает пространство на два
- 16. Работа в группах (четыре группы). Первая
- 17. Данные занести в таблицу
- 18. Слайд 18
- 19. Данные занести в таблицу24567811121314151713910161237910121314151645681117
- 20. АНАЛИЗ 1, 3, 9, 10, 16 – (это
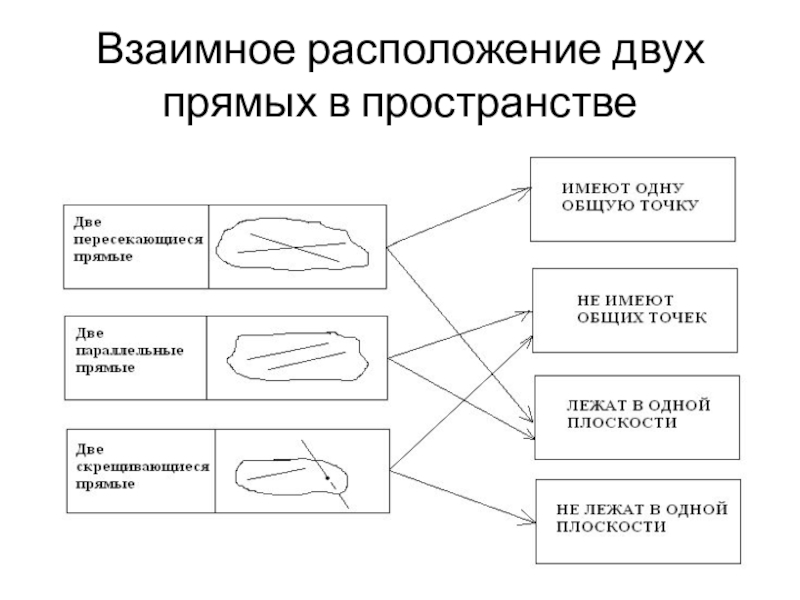
- 21. Взаимное расположение двух прямых в пространстве
- 22. Домашнее заданиеСамостоятельная работаПодготовить сообщение «Аксиомы стереометрии»
Введение в стереометриюУрок 49,50
Слайд 3Геометрия
Планиметрия
Стереометрия
stereos - телесный, твердый, объемный, пространственный
metreo - измерять
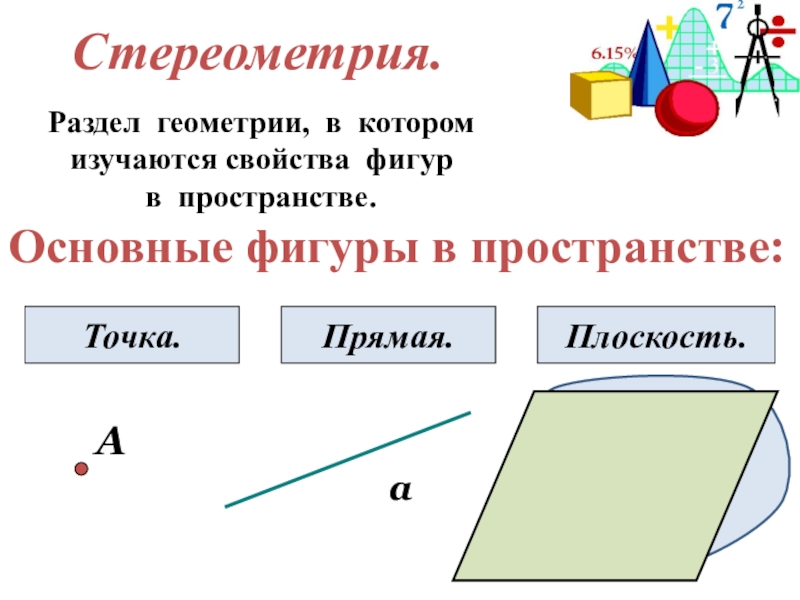
Слайд 4Стереометрия.
Раздел геометрии, в котором
изучаются свойства фигур
в пространстве.
Основные фигуры в
пространстве:
А
Точка.
а
Прямая.
Плоскость.
Слайд 5Обозначение основных
фигур в пространстве:
точка
прямая
плоскость
A, B, C, …
a, b, c, …
или
AВ,
BС, CD, …
Слайд 6Аксиома
(от греч. axíõma – принятие положения)
исходное положение научной теории, принимаемое без
доказательства
Слайд 7Аксиомы стереометрии
I. Какова бы ни была прямая, существуют точки, принадлежащие этой
прямой , и точки не принадлежащие ей.
Через любые две точки можно провести прямую, и только одну.
II. Из трех точек на прямой одна и только одна лежит между двумя другими
III. Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой
IV. Прямая, принадлежащая плоскости, разбивает плоскость на две полуплоскости
V. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 1800. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
VI. На любой полупрямой от её начальной точки можно отложить отрезок заданной длины, и только один
VII. От любой полупрямой на содержащей её плоскости в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 1800, и только один
VIII. Каков бы ни был треугольник, существует равный ему треугольник в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости
IX. На плоскости через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.
Через любые две точки можно провести прямую, и только одну.
II. Из трех точек на прямой одна и только одна лежит между двумя другими
III. Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой
IV. Прямая, принадлежащая плоскости, разбивает плоскость на две полуплоскости
V. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 1800. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
VI. На любой полупрямой от её начальной точки можно отложить отрезок заданной длины, и только один
VII. От любой полупрямой на содержащей её плоскости в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 1800, и только один
VIII. Каков бы ни был треугольник, существует равный ему треугольник в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости
IX. На плоскости через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.
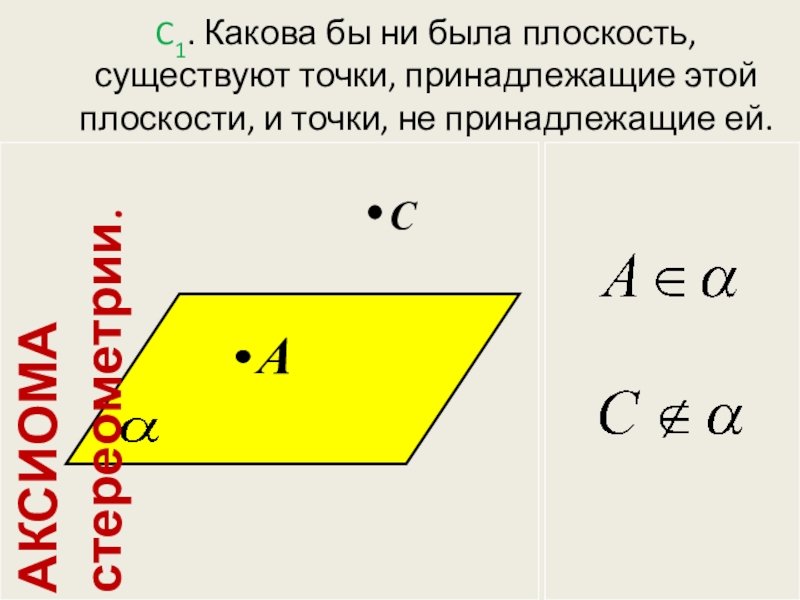
Слайд 8C1. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости,
и точки, не принадлежащие ей.
A
С
АКСИОМА стереометрии.
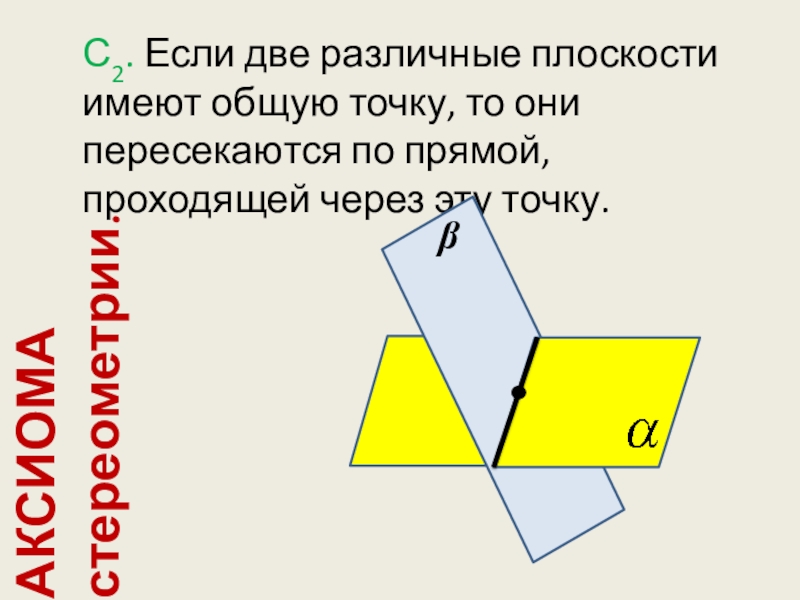
Слайд 9АКСИОМА стереометрии.
С2. Если две различные плоскости имеют общую точку, то они
пересекаются по прямой, проходящей через эту точку.
Слайд 10АКСИОМА стереометрии.
С3. Если две различные прямые имеют общую точку, то через
них можно провести плоскость, и притом только одну.
А
Слайд 12Теорема 15.1. Через прямую и не лежащую на ней точку можно
провести плоскость, и притом только одну.
Теоремы стереометрии.
В
Слайд 13Теоремы стереометрии.
Теорема 15.2. Если две точки прямой принадлежат плоскости, то вся
прямая принадлежит этой плоскости
А
В
Слайд 14Теоремы стереометрии.
Теорема 15.3.. Через три точки, не лежащие на одной прямой,
можно провести плоскость, и притом только одну.
А
В
С
Слайд 15Теорема 15.4.
Плоскость разбивает пространство на два полупространства. Если точки X
и Y принадлежат одному полупространству, то отрезок XY не пересекает плоскость.
Если же точки Х и Y принадлежат разным полупространствам, то отрезок XY пересекает плоскость.
Если же точки Х и Y принадлежат разным полупространствам, то отрезок XY пересекает плоскость.
Теоремы стереометрии.
Слайд 16Работа в группах (четыре группы).
Первая группа, из предложенных чертежей, указывает
только те, где прямые не имеют точек.
Вторая – где прямые имеют одну общую точку.
Третья – где прямые лежат в одной плоскости.
Четвертая – где прямые не лежат в одной плоскости.
Вторая – где прямые имеют одну общую точку.
Третья – где прямые лежат в одной плоскости.
Четвертая – где прямые не лежат в одной плоскости.
Слайд 20АНАЛИЗ
1, 3, 9, 10, 16 –
(это пересекающиеся прямые)
Имеют общую точку
и лежат в одной плоскости
2, 7, 12, 13, 14, 15 –
(это параллельные прямые)
Не имеют общих точек и лежат в одной плоскости
4, 5, 6, 8, 11, 17 –
(это скрещивающиеся прямые)
Не имеют общих точек и не лежат в одной плоскости.
2, 7, 12, 13, 14, 15 –
(это параллельные прямые)
Не имеют общих точек и лежат в одной плоскости
4, 5, 6, 8, 11, 17 –
(это скрещивающиеся прямые)
Не имеют общих точек и не лежат в одной плоскости.