- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Векторы в пространстве
Содержание
- 1. Презентация по геометрии Векторы в пространстве
- 2. Понятие вектора.
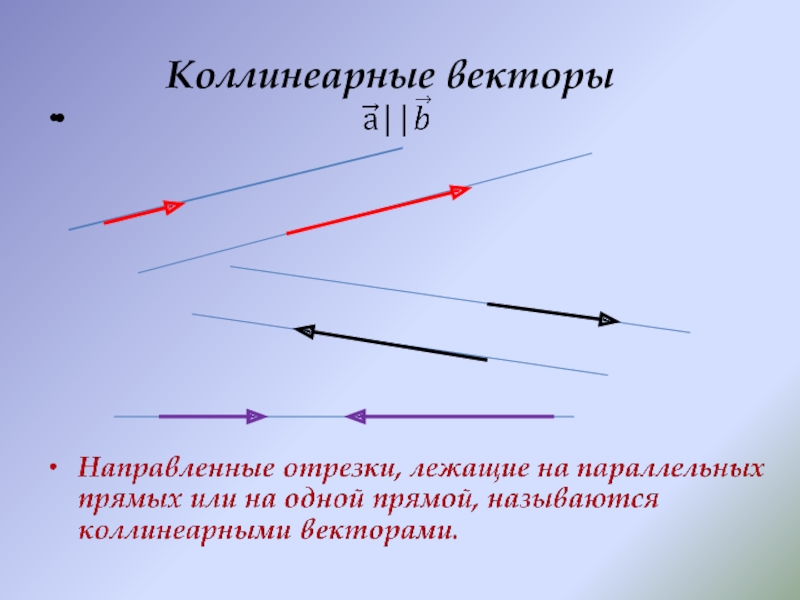
- 3. Коллинеарные векторы
- 4. Коллинеарные векторыСонаправленные векторыПротивоположно направленные векторыНулевой вектор коллинеарен любому вектору.
- 5. Равные векторы
- 6. Противоположные векторыДва вектора называются противоположными, если они имеют равные длины и противоположные направления.
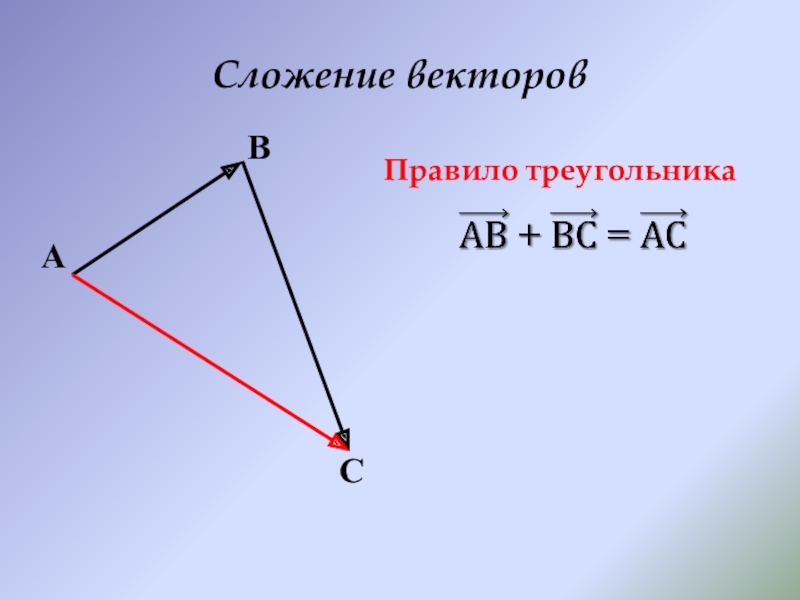
- 7. Сложение векторовАВСПравило треугольника
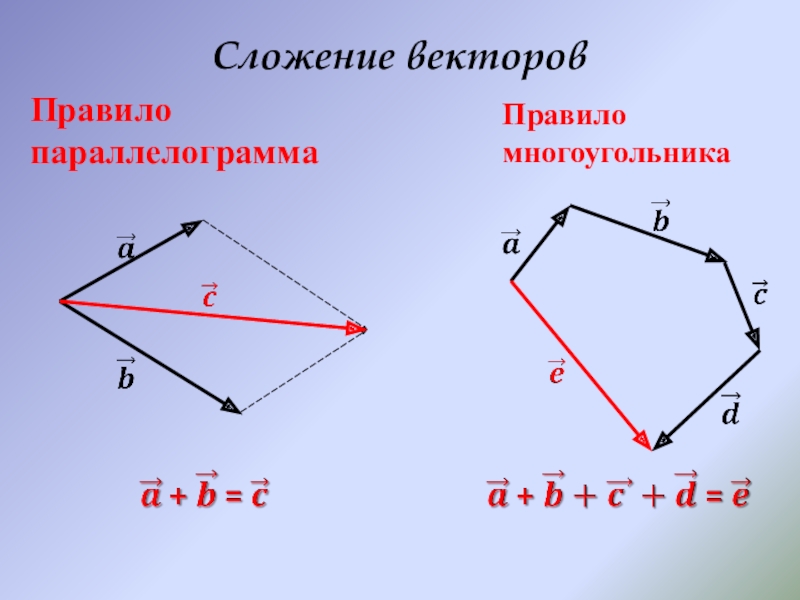
- 8. Сложение векторовПравило параллелограммаПравило многоугольника
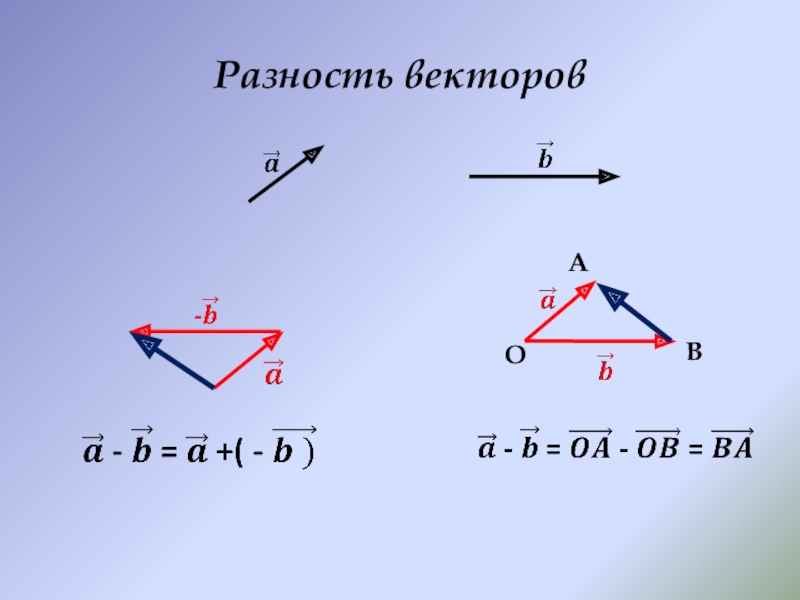
- 9. Разность векторовOAB
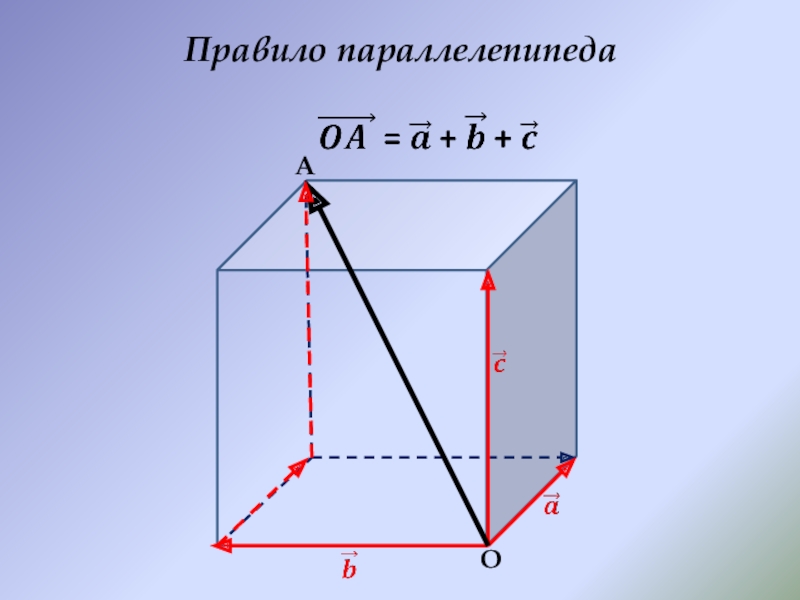
- 10. Правило параллелепипедаAO
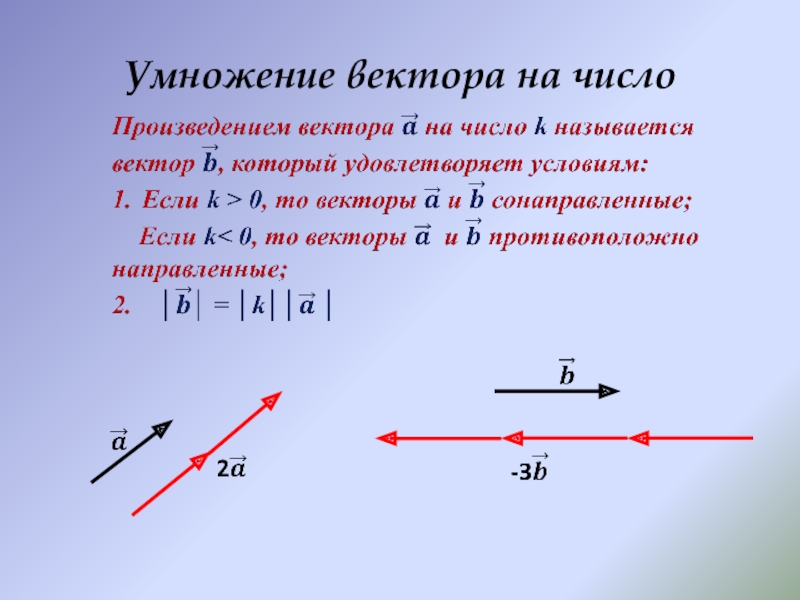
- 11. Умножение вектора на число
- 12. Свойства произведения векторовПризнак коллинеарности векторовГеометрический смысл коллинеарности векторов
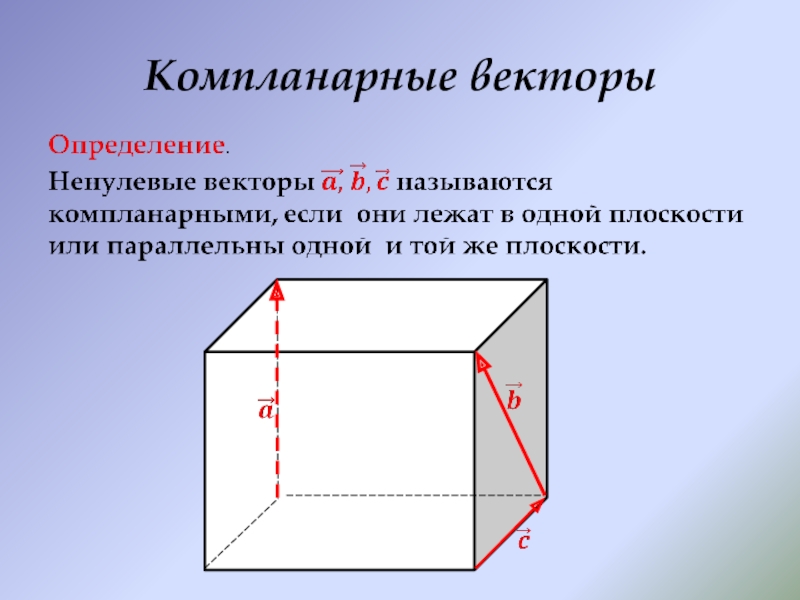
- 13. Компланарные векторы
- 14. Разложение вектора на плоскости
- 15. Признак компланарности трех векторов
- 16. Разложение вектора по трем некомпланарным векторам
- 17. Базис векторов в пространствеБазисом векторов в пространстве
- 18. Скалярное произведение векторовУгол между векторамиαα0°≤ α ≤ 180°
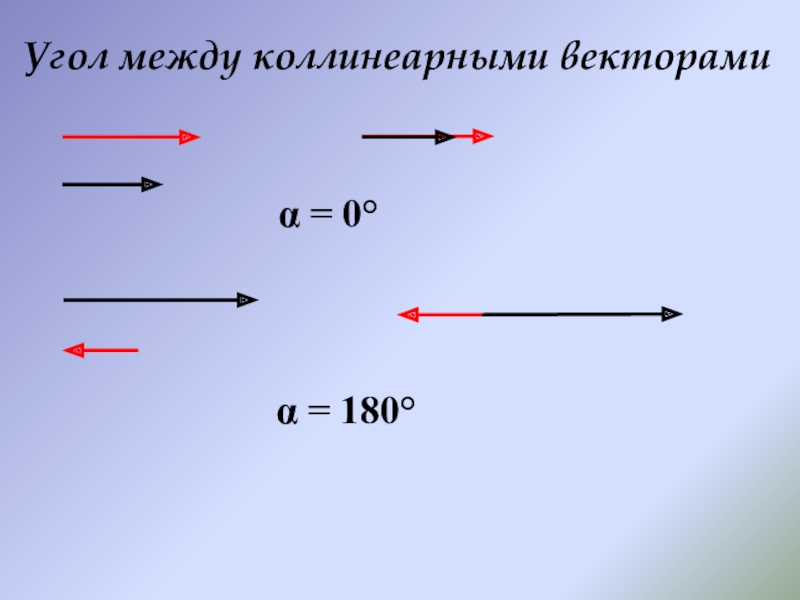
- 19. Угол между коллинеарными векторамиα = 0°α = 180°
- 20. Скалярное произведение векторовОпределение.Скалярным произведеним двух векторов называется
- 21. Скалярный квадрат векторовУгол между векторами
- 22. Свойства скалярного произведения векторовПризнак перпендикулярности двух векторов
Понятие вектора. Линейные операции над векторами
Слайд 4Коллинеарные векторы
Сонаправленные
векторы
Противоположно направленные векторы
Нулевой вектор коллинеарен любому вектору.
Слайд 6Противоположные векторы
Два вектора называются противоположными, если они имеют равные длины и
противоположные направления.
Слайд 12Свойства произведения векторов
Признак коллинеарности векторов
Геометрический смысл коллинеарности векторов
Слайд 17Базис векторов в пространстве
Базисом векторов в пространстве называется любая упорядоченная тройка
некомпланарных векторов. Векторы, образующие базис, называются базисными векторами.
Слайд 20Скалярное произведение векторов
Определение.
Скалярным произведеним двух векторов называется число, равное произведению длин
этих векторов на косинус угла между ними.
Если векторы сонаправленные, то скалярное произведение векторов равно произведению длин этих векторов.
Если векторы противоположно направленные, то скалярное произведение векторов равно минус произведению длин этих векторов.