- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Центральное и параллельное проектирование(10 класс)
Содержание
- 1. Презентация по геометрии Центральное и параллельное проектирование(10 класс)
- 2. Изображение предметов на плоскости получают различными способами:
- 3. Само восприятие человеком окружающих предметов посредством зрения
- 4. Пусть π- некоторая плоскость, S - не
- 5. Перспектива 1Центральное проектирование плоской фигуры Ф на
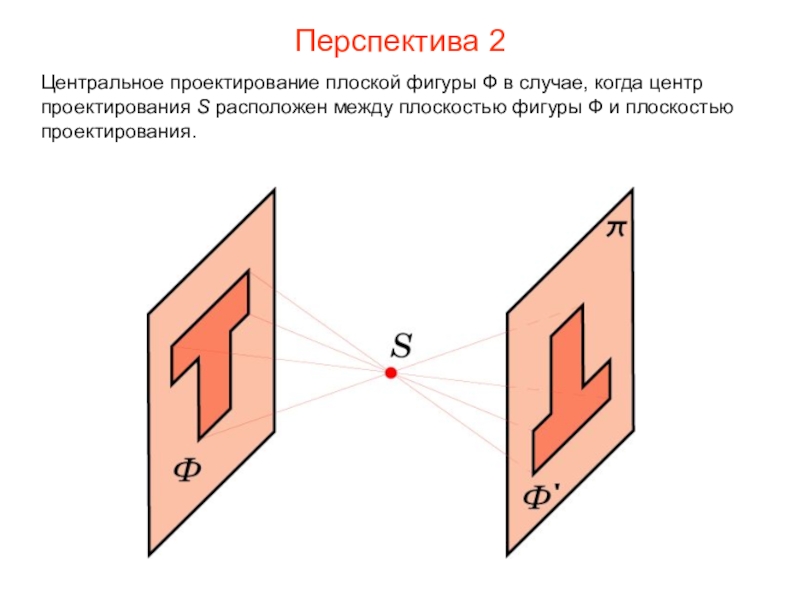
- 6. Перспектива 2Центральное проектирование плоской фигуры Ф в
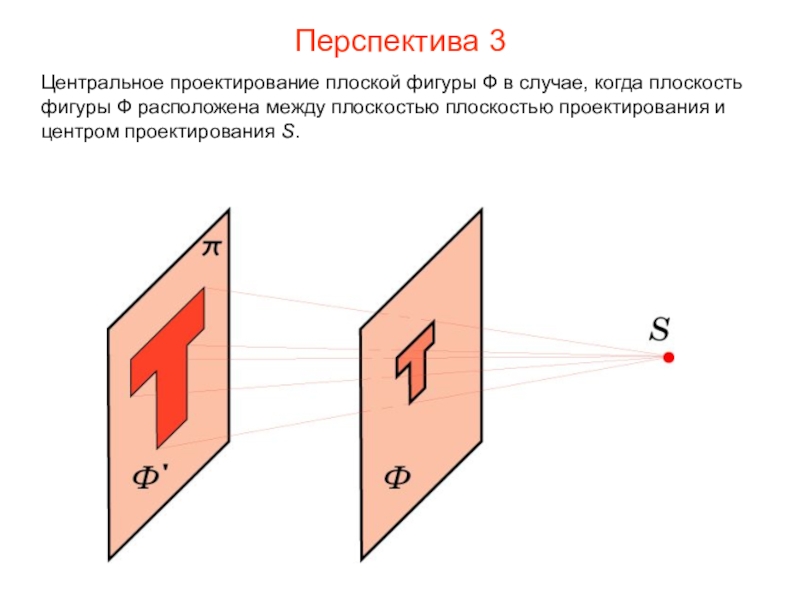
- 7. Перспектива 3Центральное проектирование плоской фигуры Ф в
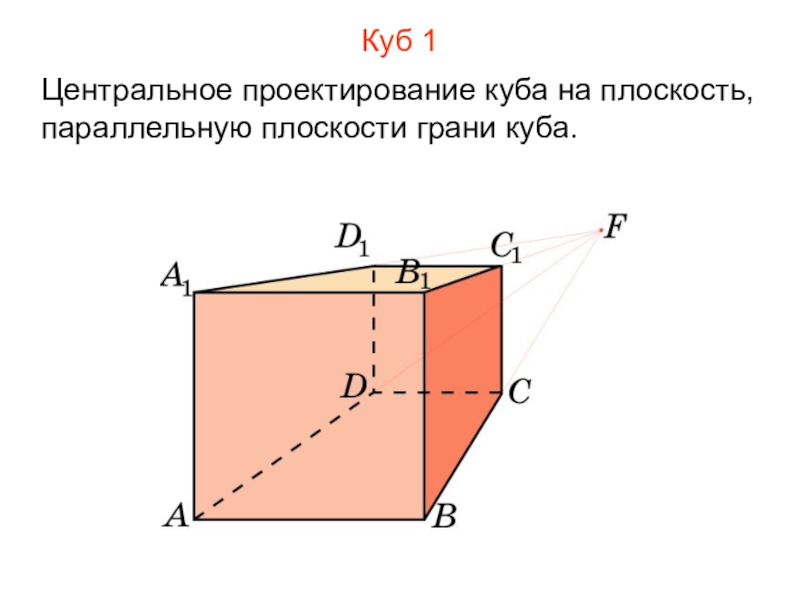
- 8. Куб 1Центральное проектирование куба на плоскость, параллельную плоскости грани куба.
- 9. А. ДюрерНа гравюре А.Дюрера (1471 – 1528) показано получение перспективного изображения предмета с помощью натянутой нити.
- 10. Н.Н. ГеРусский художник и педагог Н.Н. Ге
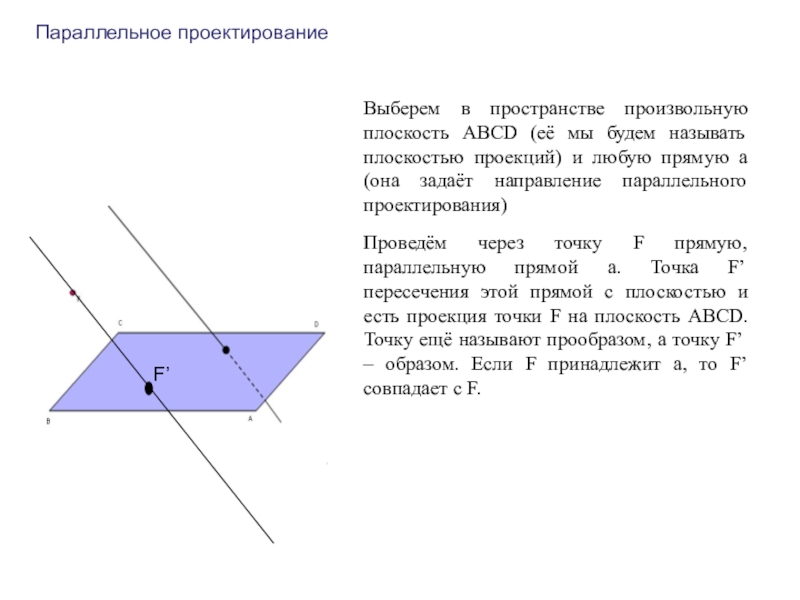
- 11. Параллельное проектированиеВыберем в пространстве произвольную плоскость ABCD
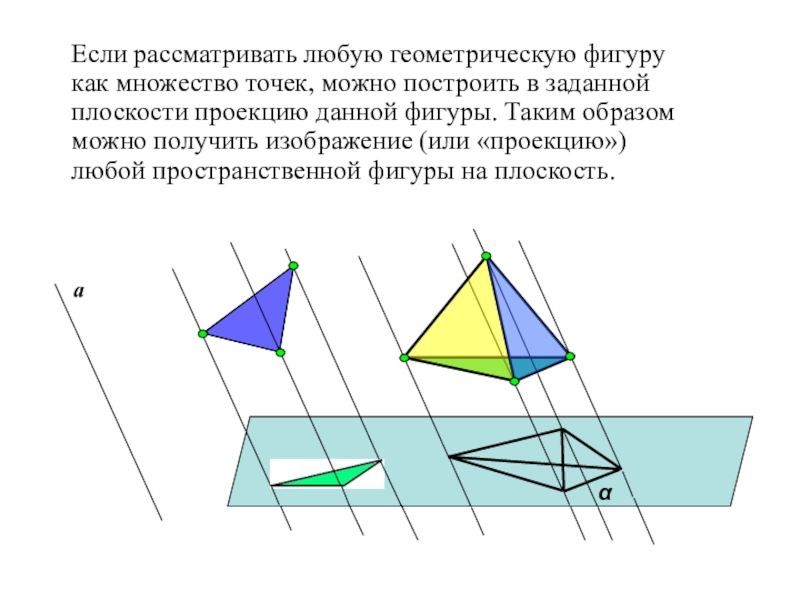
- 12. Если рассматривать любую геометрическую фигуру как множество
- 13. Изображение плоских фигур.Фигура в пространствеЕё изображение на плоскостиПроизвольный треугольникПроизвольный треугольник
- 14. Прямоугольный треугольникПроизвольный треугольникРавнобедренный треугольникПроизвольный треугольник
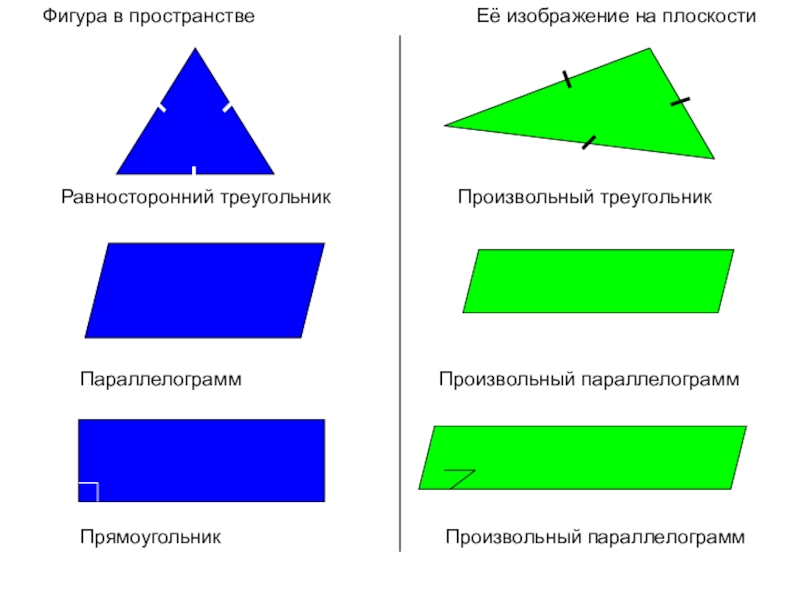
- 15. Фигура в пространствеЕё изображение на плоскостиРавносторонний треугольникПроизвольный треугольникПараллелограммПроизвольный параллелограммПрямоугольникПроизвольный параллелограмм
- 16. Фигура в пространствеЕё изображение на плоскостиКвадратПроизвольный параллелограммТрапецияПроизвольная трапецияПроизвольный параллелограммРомб
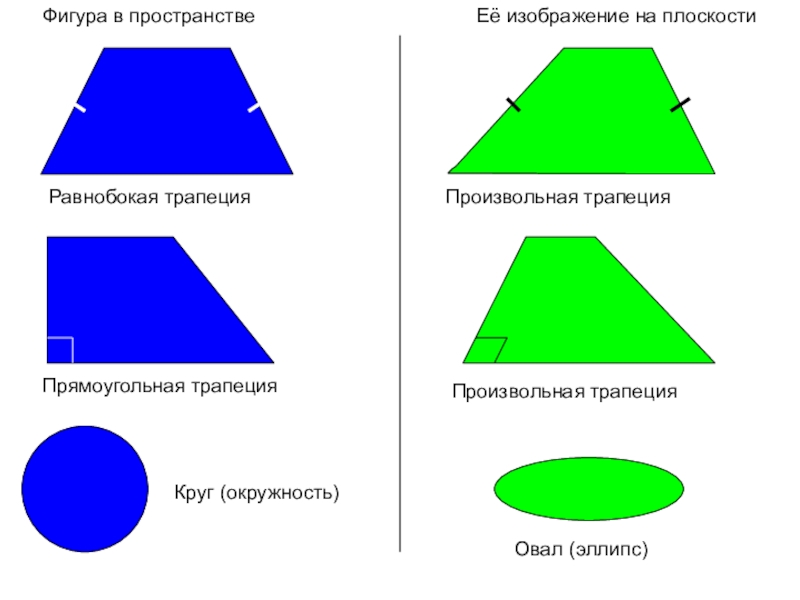
- 17. Фигура в пространствеЕё изображение на плоскостиРавнобокая трапецияПроизвольная трапецияПрямоугольная трапецияПроизвольная трапецияКруг (окружность)Овал (эллипс)
Слайд 2Изображение предметов на плоскости получают различными способами: рисованием, фотографированием и черчением.
Различают два вида проектирования:
центральное и параллельное.
Слайд 3Само восприятие человеком окружающих предметов посредством зрения осуществляется по законам центрального
Однако центральное проектирование искажает одно из основных отношений геометрии – параллельность (например, нам кажется , что железнодорожные пути сливаются на горизонте)
Центральное проектирование
Слайд 4Пусть π- некоторая плоскость, S - не принадлежащая ей точка, центр
Слайд 5Перспектива 1
Центральное проектирование плоской фигуры Ф на плоскость, находящуюся между плоскостью
Слайд 6Перспектива 2
Центральное проектирование плоской фигуры Ф в случае, когда центр проектирования
Слайд 7Перспектива 3
Центральное проектирование плоской фигуры Ф в случае, когда плоскость фигуры
Слайд 9А. Дюрер
На гравюре А.Дюрера (1471 – 1528) показано получение перспективного изображения
Слайд 10Н.Н. Ге
Русский художник и педагог Н.Н. Ге (1834 – 1894), обращаясь
Слайд 11Параллельное проектирование
Выберем в пространстве произвольную плоскость ABCD (её мы будем называть
Проведём через точку F прямую, параллельную прямой а. Точка F’ пересечения этой прямой с плоскостью и есть проекция точки F на плоскость ABCD. Точку ещё называют прообразом, а точку F’ – образом. Если F принадлежит а, то F’ совпадает с F.
F’