- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Треугольники. Теорема Пифагора
Содержание
- 1. Презентация по геометрии Треугольники. Теорема Пифагора
- 2. Слайд 2
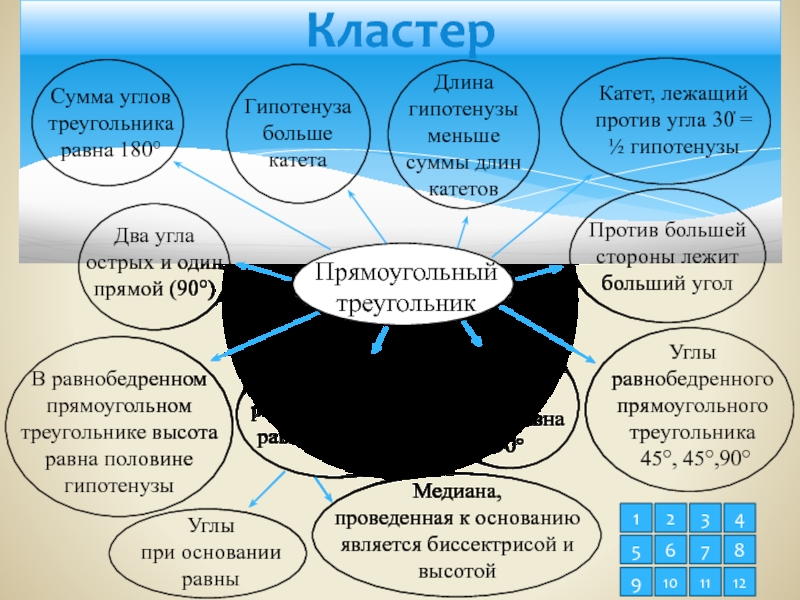
- 3. КластерПрямоугольный треугольник123456789101112
- 4. Что такое квадрат?Как вычислить площадь квадрата?Чему равна
- 5. Как вычислить площадь прямоугольного треугольника?Чему равна площадь
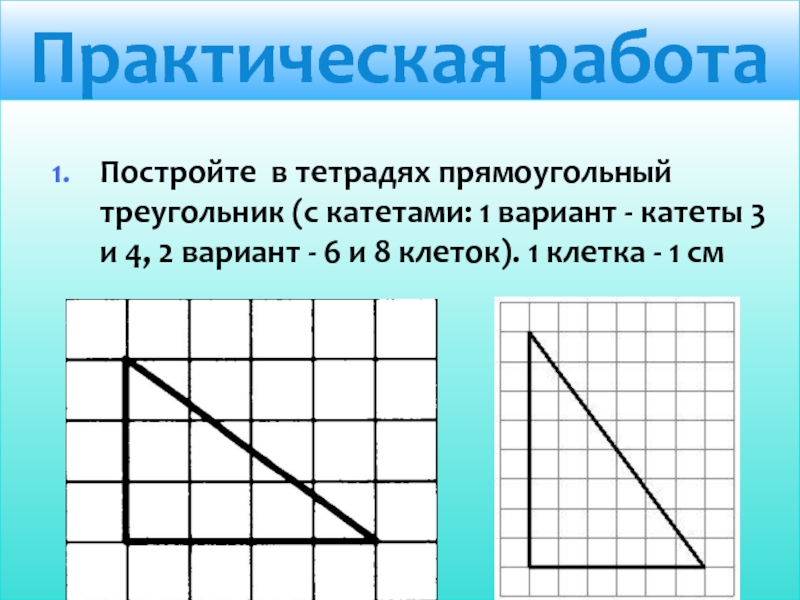
- 6. Практическая работаПостройте в тетрадях прямоугольный треугольник (с
- 7. Практическая работаИзмерьте гипотенузу. Результаты измерений запишите в
- 8. Зависимость, которую мы с вами установили, в геометрии называют теоремой Пифагора.a2 + b2 = с2
- 9. Древнегреческий философ и математик(580 - 500 г. до н.э.)Пифагор
- 10. Теорема Пифагора. Теорема Пифагора - важнейшее
- 11. Дано:Прямоугольный треугольника, в – катетыс- гипотенузаДоказать:с2=а2+b2ccccc 2 bababaДоказательство
- 12. Треугольник со сторонами 3, 4 и 5
- 13. По мнению
- 14. С древних времён известен очень простой способ построения прямых углов на местности.Принцип работы гарпедонаптов:
- 15. На изображении видим три разных круга с
- 16. В теорему Пифагора можно подставлять абсолютно любые
- 17. Теорема Пифагора широко применяется в строительстве, архитектуре и мобильной связи.
- 18. При строительстве домов и коттеджей часто встает
- 19. При строительстве мостов, дорог рассчитывают подъемы и спуски.
- 20. В прямоугольном треугольнике катеты равны 30 см
- 21. Задача:cabДано:Прямоугольный треугольника, в – катетыс- гипотенузаb=6м, c=10мНайти:Длину катета a
- 22. Самостоятельная работа1 ) Треугольник АВС - прямоугольный.
- 23. Решение:1) AB² = AC² + CB²
- 24. 1) Как формулируется теорема Пифагора?2) К любым
- 25. «Я повторил…»«Я узнал…»«Я научился решать…»«Мне понравилось…»«Теорема Пифагора звучит так…»Замечательная теорема
- 26. П. 54, № 483 (б), 484 (а).Исследовательская
- 27. Спасибо за внимание!
Слайд 4Что такое квадрат?
Как вычислить площадь квадрата?
Чему равна площадь квадрата, если его
Как называются стороны прямоугольного треугольника?
Назовите катеты и гипотенузу прямоугольного АВС с прямым углом С
Прямоугольник, у которого все стороны равны.
S = a2
16 см2; b2 см2; (a2+2ab+b2) см2
Два катета и гипотенуза.
AC, BC – катеты, AB –гипотенуза
Текущее повторение
A
B
C
Слайд 5
Как вычислить площадь прямоугольного треугольника?
Чему равна площадь прямоугольного треугольника с катетами
Площадь прямоугольного треугольника равна 20 см2, один из катетов 5 см. Найдите неизвестный катет.
Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника.
Половина произведения катетов
S = 21 см2
S = ½ ab
b = 8 см
c =? см
Текущее повторение
Слайд 6Практическая работа
Постройте в тетрадях прямоугольный треугольник (с катетами: 1 вариант -
Слайд 7Практическая работа
Измерьте гипотенузу. Результаты измерений запишите в тетрадях.
У всех ли получилось,
5
10
Слайд 8Зависимость, которую мы с вами установили, в геометрии называют теоремой Пифагора.
a2
Слайд 10Теорема Пифагора.
Теорема Пифагора - важнейшее утверждение геометрии.
Теорема
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Слайд 11Дано:
Прямоугольный треугольник
а, в – катеты
с- гипотенуза
Доказать:
с2=а2+b2
c
c
c
c
c 2
b
a
b
a
b
a
Доказательство Пифагора
b
b
a
Доказательство:
1) Достроим треугольник до
стороной а + в.
4) Тогда, 2ав+с2=(а+в) 2
2ав+с2=а2+2ав+в2
Вычтем из обеих частей 2ав, тогда:
с2=а2+в2,что и требовалось доказать.
+с2=2ав+с2
Слайд 12Треугольник со сторонами 3, 4 и 5 часто называют
египетским треугольником
т.
Существует бесчисленное множество целых положительных чисел,
удовлетворяющих соотношению
с2 = а2 + b2.
Они называются Пифагоровыми числами.
Интересные факты:
Слайд 13 По мнению крупнейшего немецкого историка математики
М. Кантора 1829 — 1920), (в Древнем Египте существовала особая профессия гарпедонаптов — «натягивателей веревок», которые во время торжественной церемонии закладки храмов и пирамид размечали прямые углы с помощью веревки, имеющей 12 (= 3 + 4 + 5) равноотстоящих узлов.
Историческая справка:
Слайд 14С древних времён известен очень простой способ построения прямых углов на
Принцип работы гарпедонаптов:
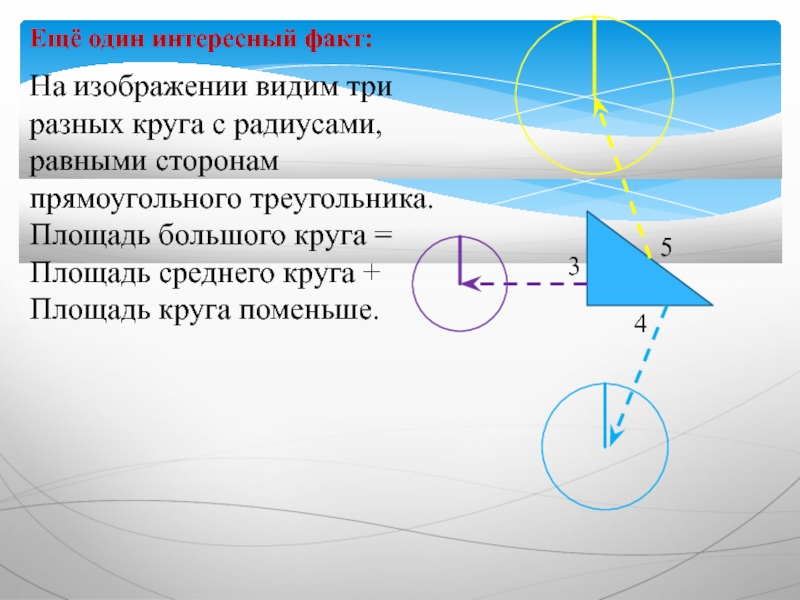
Слайд 15На изображении видим три разных круга с радиусами, равными сторонам
прямоугольного треугольника.
Ещё
4
3
5
Площадь большого круга = Площадь среднего круга + Площадь круга поменьше.
Слайд 16В теорему Пифагора можно подставлять абсолютно любые цифры. Она может помочь
Пример из жизни:
Слайд 18При строительстве домов и коттеджей часто встает вопрос о длине стропил
При строительстве лестниц необходимо рассчитать длину, ширину каждой ступени, крутизну лестницы.
Слайд 20В прямоугольном треугольнике катеты равны 30 см и 40 см. Найдите
Задача
a=30
c-?
b=40
Решение:
c2 = a2 + b2
c2 = 302 + 402
c2 = 900+1600
c2 = 2500
c =50,
c =-50(не имеет смысла)
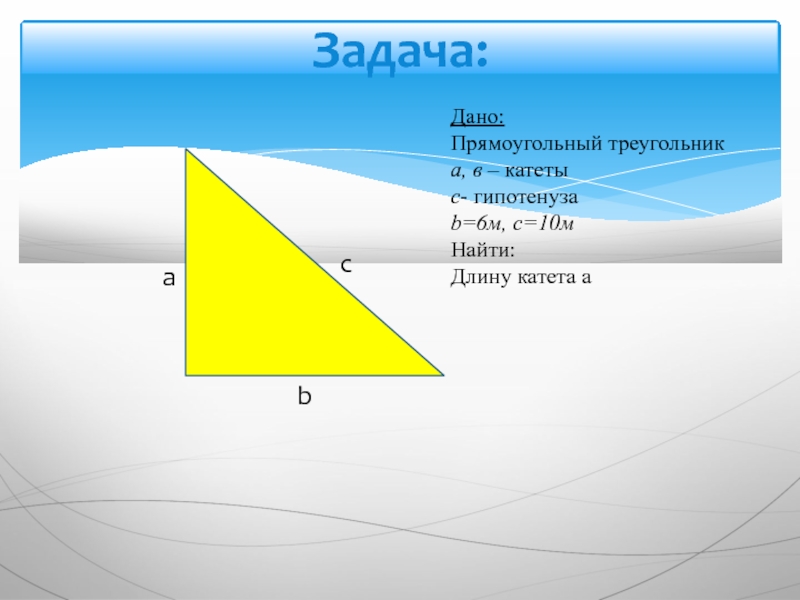
Слайд 21Задача:
c
a
b
Дано:
Прямоугольный треугольник
а, в – катеты
с- гипотенуза
b=6м, c=10м
Найти:
Длину катета a
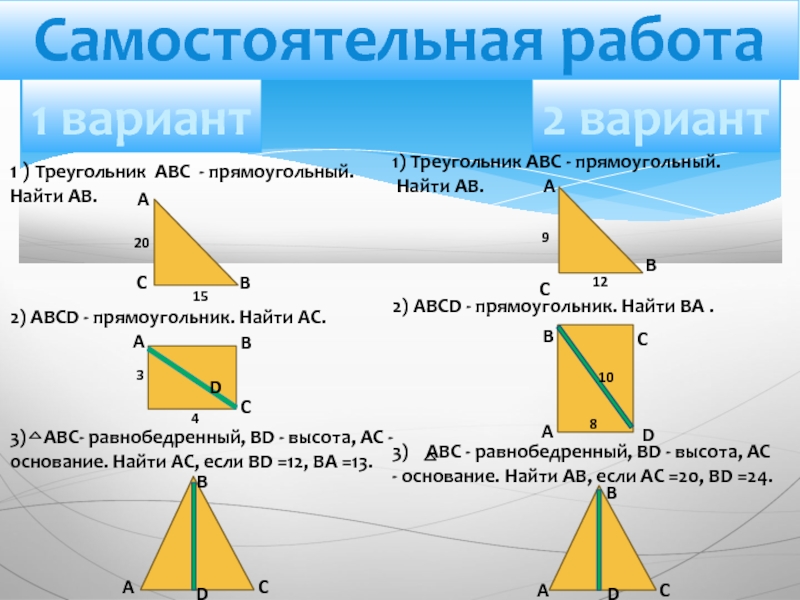
Слайд 22Самостоятельная работа
1 ) Треугольник АВС - прямоугольный. Найти АВ.
2)
3) АВС- равнобедренный, BD - высота, АС - основание. Найти АС, если BD =12, BA =13.
1 вариант
2 вариант
1) Треугольник АВС - прямоугольный.
Найти АВ.
2) ABCD - прямоугольник. Найти BA .
3) АВС - равнобедренный, BD - высота, АС - основание. Найти АВ, если АС =20, BD =24.
A
B
C
15
20
A
B
C
D
4
3
A
B
C
A
B
C
9
12
A
B
C
D
8
D
A
B
C
D
10
Слайд 23Решение:
1) AB² = AC² + CB²
AB² = 20²
AB² = 625
AB = 25
2) ACD - прямоугольный
AC² = AD² + DC²
AC² = 4² + 3²
AC² = 25
AC = 5
3) ABD - прямоугольный
AD² = AB² - BD²
AD² = 13² - 12²
AD² = 25
AD = 5
AC = 2AD = 2 * 5 = 10
1 вариант
1) AB² = AC² + CB²
BC² = 12² + 9²
BC² = 225
BC = 15
2) BAD - прямоугольный
BA² = BD² - AD²
BA² = 10² - 8²
BA² = 36
BA = 6
3) ABD - прямоугольный
AD = ½AC = 10;
AB² = AD² + BD²
AB² = 10² + 24²
AB² = 676
AB = 26
2 вариант
Слайд 241) Как формулируется теорема Пифагора?
2) К любым ли треугольникам ее можно
Ответьте на вопросы устно:
Назовите треугольники, к которым применима теорема Пифагора?
Слайд 25«Я повторил…»
«Я узнал…»
«Я научился решать…»
«Мне понравилось…»
«Теорема Пифагора звучит так…»
Замечательная теорема
Слайд 26П. 54, № 483 (б), 484 (а).
Исследовательская работа:
«Существуют ли
доказательства теоремы?»
Домашнее задание