- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Трапеция 8 класс
Содержание
- 1. Презентация по геометрии Трапеция 8 класс
- 2. Цели урокаРассмотреть теорему о площади трапеции и
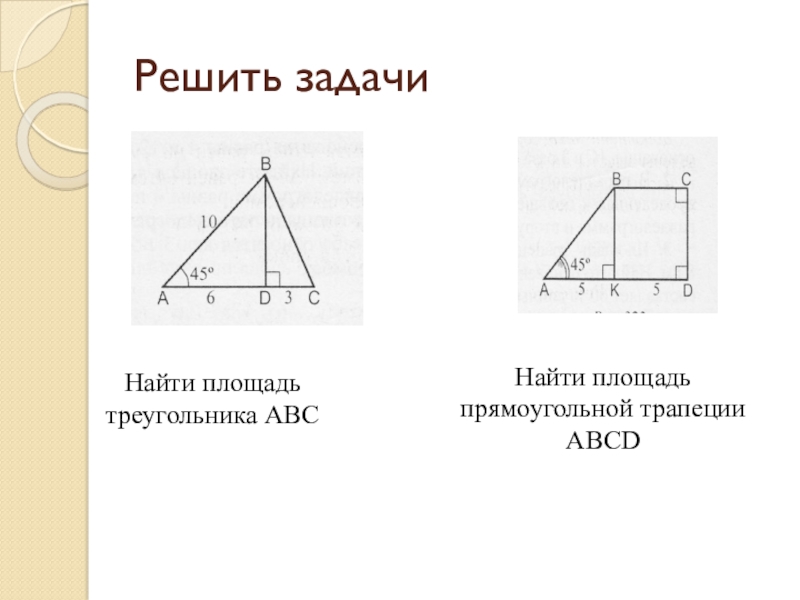
- 3. Решить задачиНайти площадь треугольника АВСНайти площадь прямоугольной трапеции АВСD
- 4. Решить задачу Найдите площадь трапеции АВСD,
- 5. Слайд 5
- 6. Теорема: Площадь трапеции равна произведению полусуммы ее
- 7. Дано: АВСD – трапеция, АD и ВС
- 8. Учебник (устно)№480 (а)Найдите площадь трапецииАВСD c основаниями
- 9. Учебник (письменно)№482Дано: АВСD-трапеция, АВ=СD, ∟В=135˚, ВК- высота,
- 10. Решить самостоятельноПериметр равнобедренной трапеции равен 32 см,
- 11. Итог урокаЧто нового узнали на уроке?Как найти площадь трапеции?Кто лучше всех работал?Что понравилось на уроке?
- 12. Домашнее заданиеПункт 53,вопрос 7Повторить формулы для вычисления площади прямоугольника, квадрата, параллелограмма, ромба, треугольника, трапеции;№480(б), 481
Слайд 2Цели урока
Рассмотреть теорему о площади трапеции и показать ее применение в
Совершенствовать навыки решения задач
Слайд 4Решить задачу
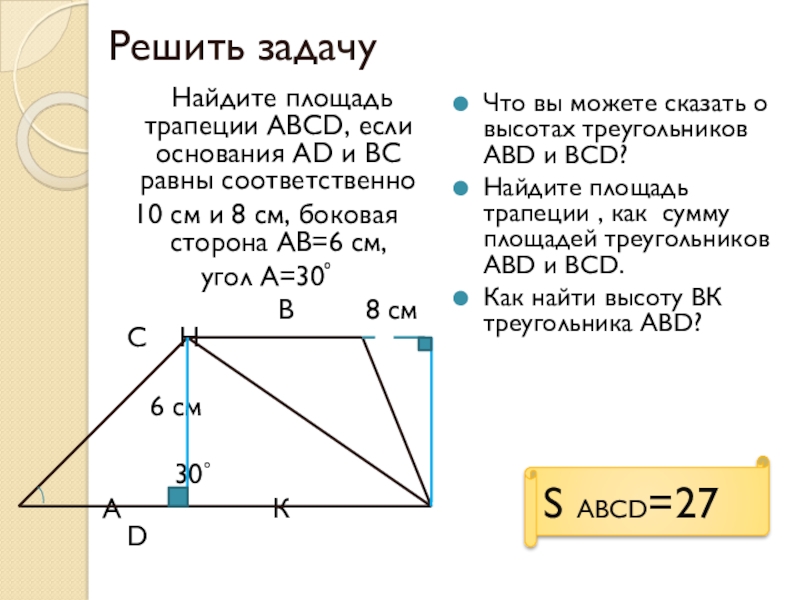
Найдите площадь трапеции АВСD, если основания AD и
10 см и 8 см, боковая сторона АВ=6 см,
угол А=30˚
В 8 см С Н
6 см
30˚
А К D
Что вы можете сказать о высотах треугольников АВD и BCD?
Найдите площадь трапеции , как сумму площадей треугольников АВD и BCD.
Как найти высоту ВК треугольника АВD?
S ABCD=27
Слайд 5
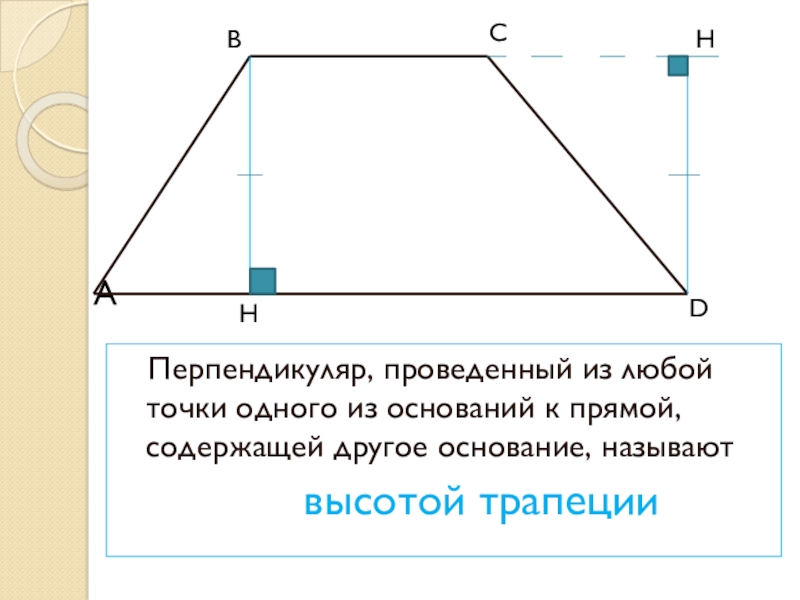
Перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание, называют
высотой трапеции
В
H
C
H
D
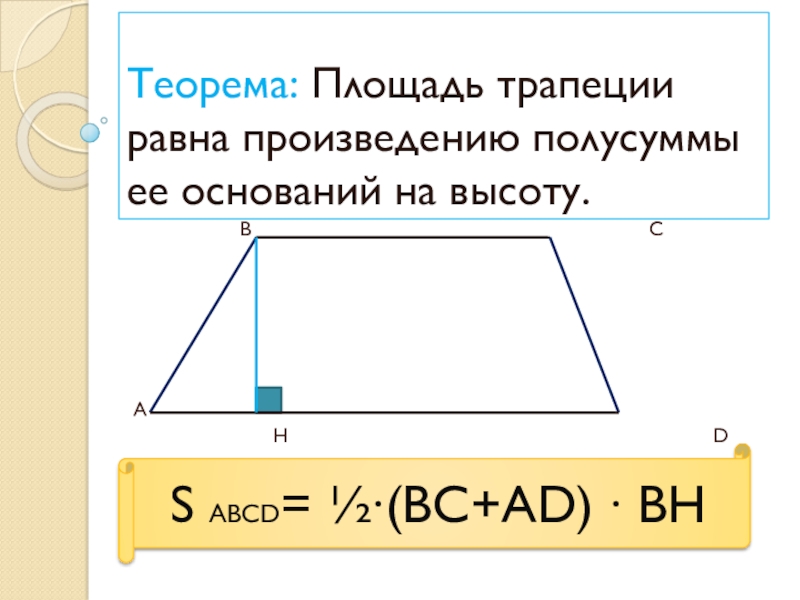
Слайд 6Теорема: Площадь трапеции равна произведению полусуммы ее оснований на высоту.
В С
А
Н D
S ABCD= ½∙(BC+AD) ∙ ВН
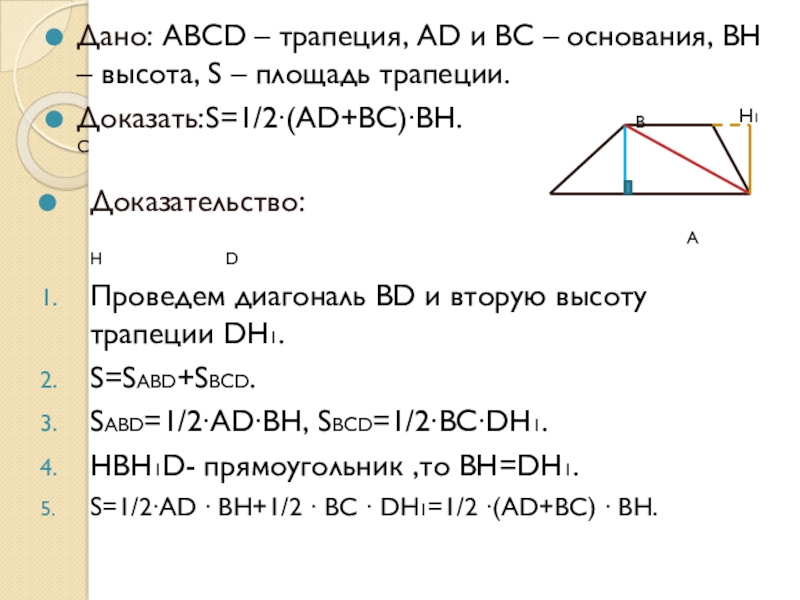
Слайд 7Дано: АВСD – трапеция, АD и ВС – основания, ВН –
Доказать:S=1/2∙(AD+BC)∙BН. В С
Доказательство:
А Н D
Проведем диагональ ВD и вторую высоту трапеции DН1.
S=SABD+SBCD.
SABD=1/2∙AD∙BH, SBCD=1/2∙BC∙DH1.
HBH1D- прямоугольник ,то BH=DH1.
S=1/2∙AD ∙ BH+1/2 ∙ BC ∙ DH1=1/2 ∙(AD+BC) ∙ BH.
Н1
Слайд 8Учебник (устно)
№480 (а)
Найдите площадь трапеции
АВСD c основаниями АВ и CD, если:
АВ=21
S=1/2∙(21+17) ∙ 7=
133
Слайд 9Учебник (письменно)
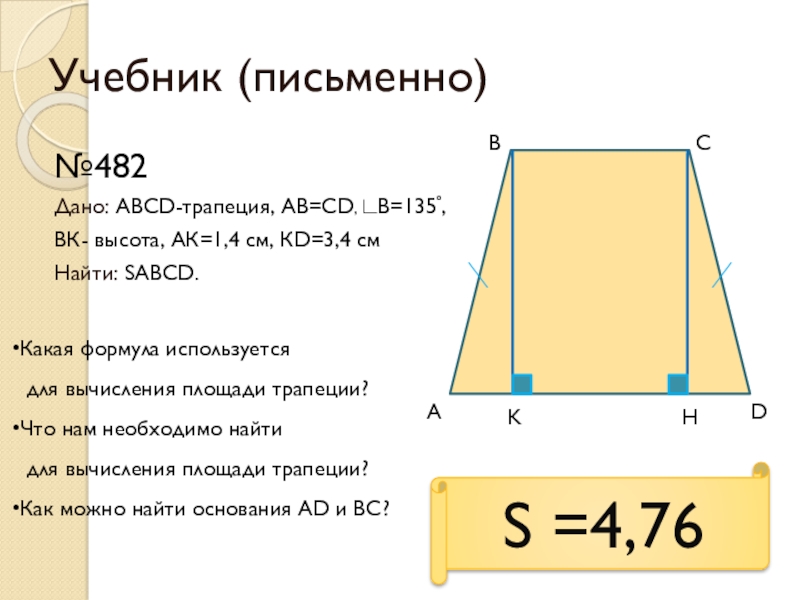
№482
Дано: АВСD-трапеция, АВ=СD, ∟В=135˚,
ВК- высота, АК=1,4 см, КD=3,4 см
Найти:
Какая формула используется
для вычисления площади трапеции?
Что нам необходимо найти
для вычисления площади трапеции?
Как можно найти основания АD и ВС?
S =4,76
C
B
D
A
K
H
Слайд 10Решить самостоятельно
Периметр равнобедренной трапеции равен 32 см, боковая сторона 5 см,
В трапеции ABCD основания AD и ВС равны 10 см и 8 см соответственно. Площадь треугольника ABD равна 30 см² .Найдите площадь трапеции.
4
54
Слайд 11Итог урока
Что нового узнали на уроке?
Как найти площадь трапеции?
Кто лучше всех
Что понравилось на уроке?
Слайд 12Домашнее задание
Пункт 53,вопрос 7
Повторить формулы для вычисления площади прямоугольника, квадрата, параллелограмма,
№480(б), 481