- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Повторение. Часть 3. Треугольники, площадь (8 класс )
Содержание
- 1. Презентация по геометрии Повторение. Часть 3. Треугольники, площадь (8 класс )
- 2. Повторяем теориюКакие пять изученных нами отрезков (линий)
- 3. Повторяем теориюВАСколько медиан можно провести в каждом
- 4. Повторяем теориюВАСколько биссектрис можно провести в каждом
- 5. Повторяем теориюВАСколько их можно провести в каждом
- 6. Повторяем теориюВАСколько высот можно провести в каждом
- 7. AB*CC1= BC*AA1=
- 8. Домашнее задание (Для домашнего задания использованы
Слайд 1Повторение 8 класс
часть 3
треугольники
Лаптева Ю.А.
Учитель математики МБОУ СОШ №3,
Слайд 2Повторяем теорию
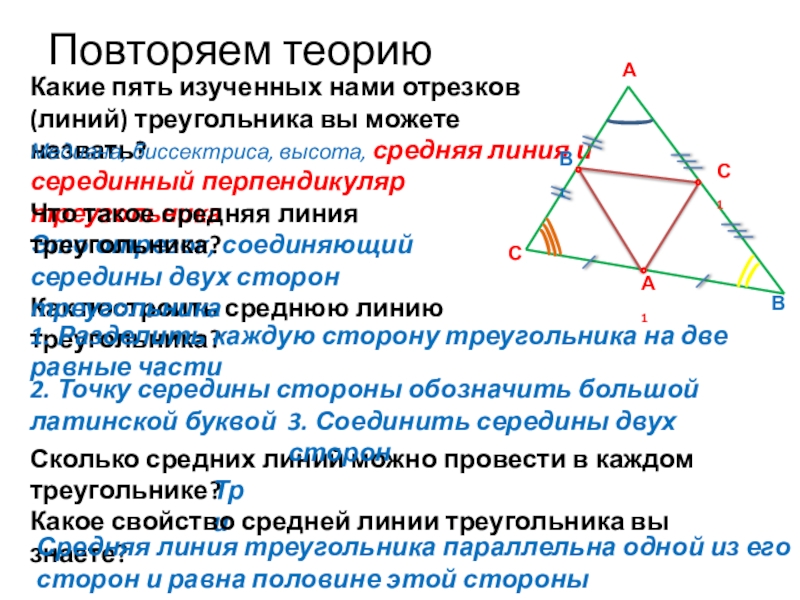
Какие пять изученных нами отрезков (линий) треугольника вы можете назвать?
Медиана,
В
А
Сколько средних линий можно провести в каждом треугольнике?
Как построить среднюю линию треугольника?
1. Разделить каждую сторону треугольника на две равные части
С
Это отрезок, соединяющий середины двух сторон треугольника
3. Соединить середины двух сторон
2. Точку середины стороны обозначить большой латинской буквой
Что такое средняя линия треугольника?
В1
А1
С1
Три
Какое свойство средней линии треугольника вы знаете?
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны
Слайд 3Повторяем теорию
В
А
Сколько медиан можно провести в каждом треугольнике?
Как построить медиану треугольника?
1.
С
Это отрезок, соединяющий вершину и середину противоположной стороны
3. Соединить середину стороны с противолежащей вершиной
2. Точку середины стороны обозначить большой латинской буквой
Вспомните что такое медиана?
В1
А1
С1
Три
Какие свойства медиан треугольника вы знаете?
Медианы треугольника пересекаются в одной точке
О
Медианы треугольника точкой пересечения делятся в пропорции 2:1
Решите задачу: Медианы треугольника , проведенные из вершин А и С равны соответственно 15 и 12 см, сторона АС равна 8 см, О - точка пересечения медиан. Найдите стороны треугольника АОС.
Слайд 4Повторяем теорию
В
А
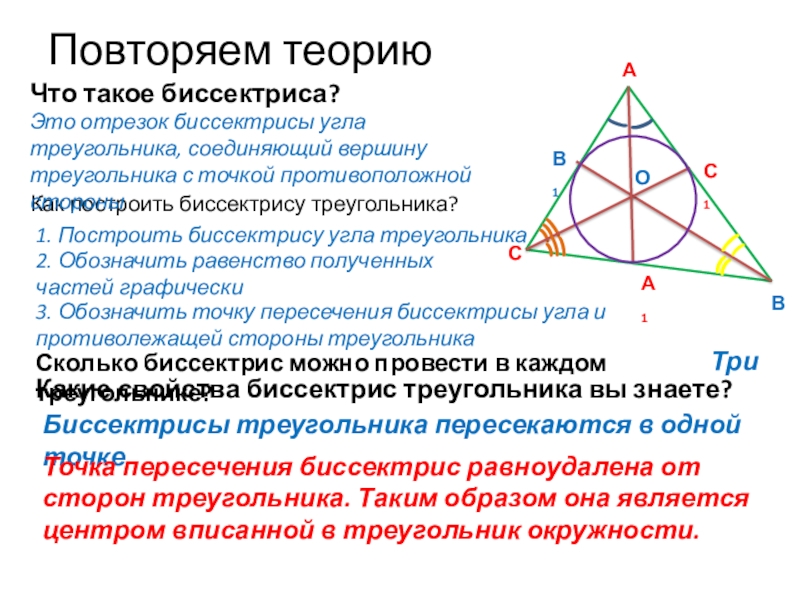
Сколько биссектрис можно провести в каждом треугольнике?
Как построить биссектрису треугольника?
1.
С
Это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны
3. Обозначить точку пересечения биссектрисы угла и противолежащей стороны треугольника
2. Обозначить равенство полученных частей графически
Что такое биссектриса?
В1
А1
С1
Три
Какие свойства биссектрис треугольника вы знаете?
Биссектрисы треугольника пересекаются в одной точке
О
Точка пересечения биссектрис равноудалена от сторон треугольника. Таким образом она является центром вписанной в треугольник окружности.
Слайд 5Повторяем теорию
В
А
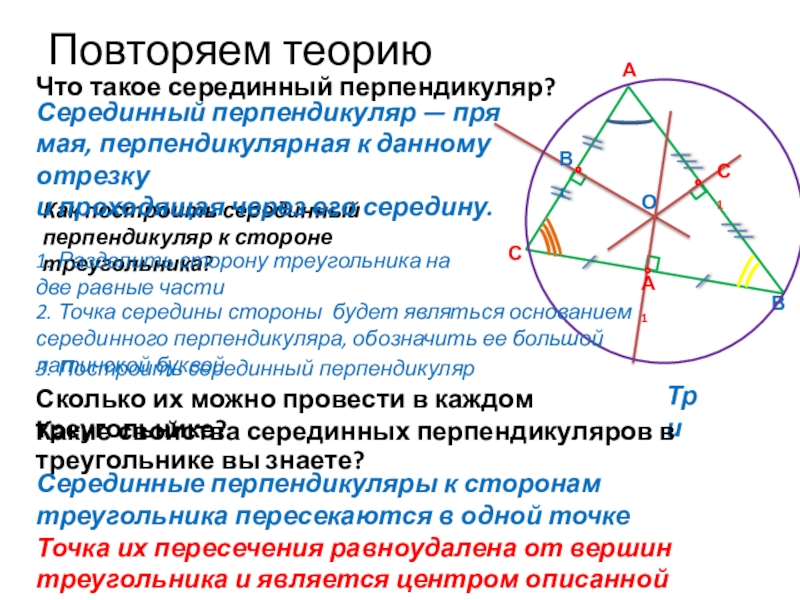
Сколько их можно провести в каждом треугольнике?
Как построить серединный перпендикуляр
1. Разделить сторону треугольника на две равные части
С
Серединный перпендикуляр — прямая, перпендикулярная к данному отрезку и проходящая через его середину.
3. Построить серединный перпендикуляр
Что такое серединный перпендикуляр?
В1
А1
С1
Три
Какие свойства серединных перпендикуляров в треугольнике вы знаете?
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке
О
Точка их пересечения равноудалена от вершин треугольника и является центром описанной окружности
2. Точка середины стороны будет являться основанием серединного перпендикуляра, обозначить ее большой латинской буквой
Слайд 6Повторяем теорию
В
А
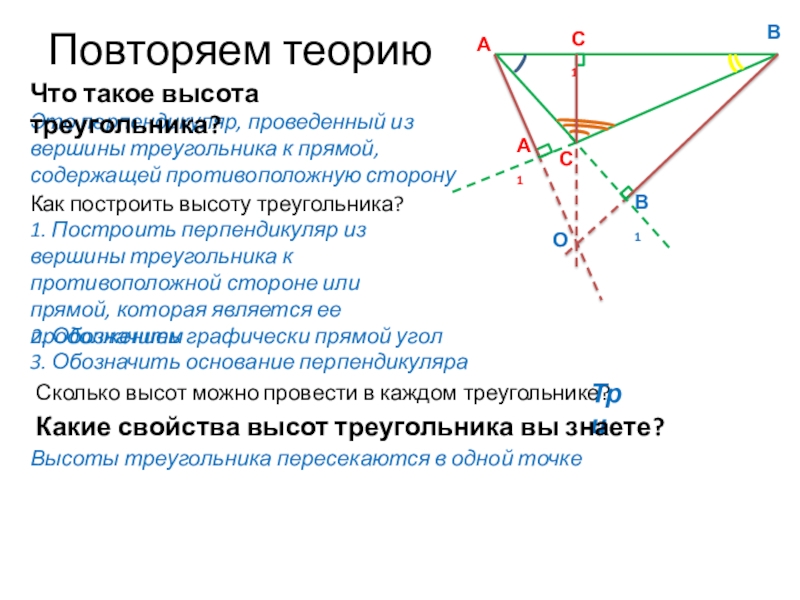
Сколько высот можно провести в каждом треугольнике?
Как построить высоту треугольника?
1.
С
Это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону
3. Обозначить основание перпендикуляра
2. Обозначить графически прямой угол
Что такое высота треугольника?
В1
А1
С1
Три
Какие свойства высот треугольника вы знаете?
Высоты треугольника пересекаются в одной точке
О
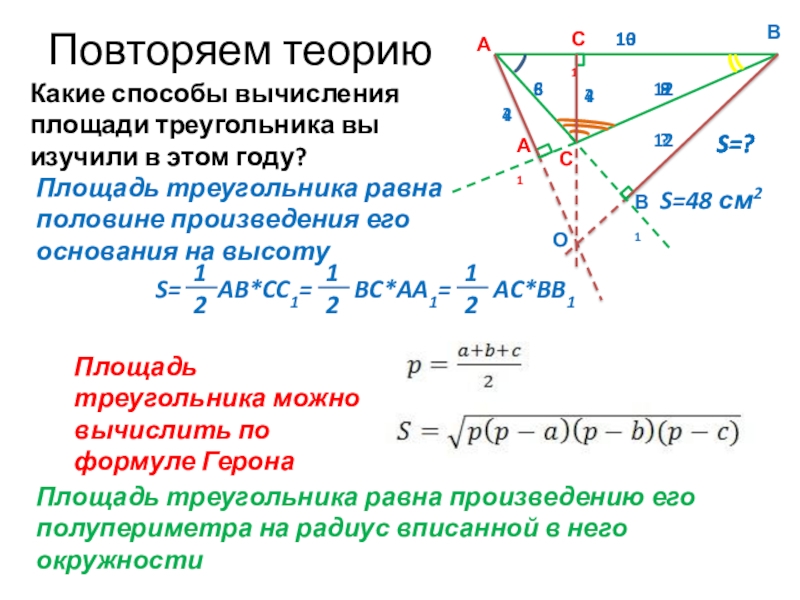
Слайд 7 AB*CC1= BC*AA1= AC*BB1
1
2
1
2
1
2
Повторяем теорию
Площадь треугольника равна половине произведения его основания на высоту
Какие способы вычисления площади треугольника вы изучили в этом году?
Площадь треугольника равна произведению его полупериметра на радиус вписанной в него окружности
Площадь треугольника можно вычислить по формуле Герона
S=
В
А
С
В1
А1
С1
О
4
10
9
12
4
6
6
8
S=?
S=?
S=?
S=?
10
12
8
16
S=48 см2
?
?
?
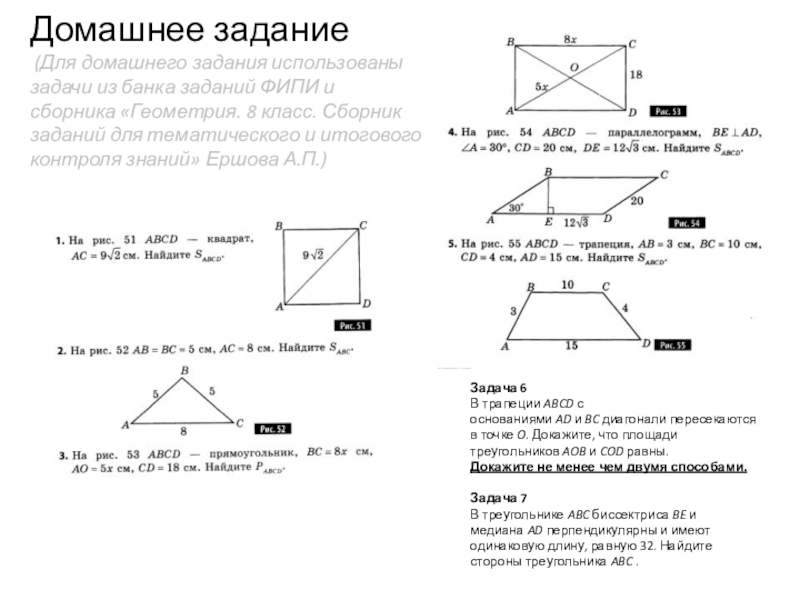
Слайд 8Домашнее задание (Для домашнего задания использованы задачи из банка заданий ФИПИ
Задача 6
В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O. Докажите, что площади треугольников AOB и COD равны.
Докажите не менее чем двумя способами.
Задача 7
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 32. Найдите стороны треугольника ABC .