- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Октаэдр (10 класс)
Содержание
- 1. Презентация по геометрии Октаэдр (10 класс)
- 2. ПРАВИЛЬНЫЙ ОКТАЭДРОктаэдр - геометрическое тело, ограниченное 8
- 3. Сумма ребер
- 4. Слайд 4
- 5. 3.В октаэдр можно вписать куб, притом все
- 6. Примеры
- 7. Октаэдр является одним из пяти платоновых
- 8. Немецкий математик и астроном Иоганн Кеплер (1571
- 9. Кубок КеплераГод за годом он уточнял свои
- 10. Слайд 10
- 11. Куприт (красная медная руда)МалахитПеровскит
- 12. 1)Монокристаллы алюмокалиевых квасцов имеют форму октаэдра. Они
- 13. Слайд 13
- 14. Из каких фигур составлен октаэдр?Из равносторонних треугольников.Сколько
- 15. Ресурсы:http://polyhedron2008.narod.ru/pages/octa.htmhttp://licey102.k26.ru/dist-kurs/p6aa1.htmhttp://ru.wikipedia.org/wiki/%D0%9E%D0%BA%D1%82%D0%B0%D1%8D%D0%B4%D1%80Учебник «ГЕОМЕТРИЯ, 10-11», авторы: Л. С. Атанасян, В. Ф. Бутузов и др.
Слайд 1ОКТАЭДР
Презентация к урокам геометрии 10 класса.
Каторова О.Г.,
учитель математики
МБОУ Гимназии №
Слайд 2ПРАВИЛЬНЫЙ ОКТАЭДР
Октаэдр - геометрическое тело, ограниченное 8 равносторонними треугольниками (греч. «окто»
Октаэдр имеет 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра (4 треугольника), т.е. сумма плоских углов при вершине составляет 240 градусов.
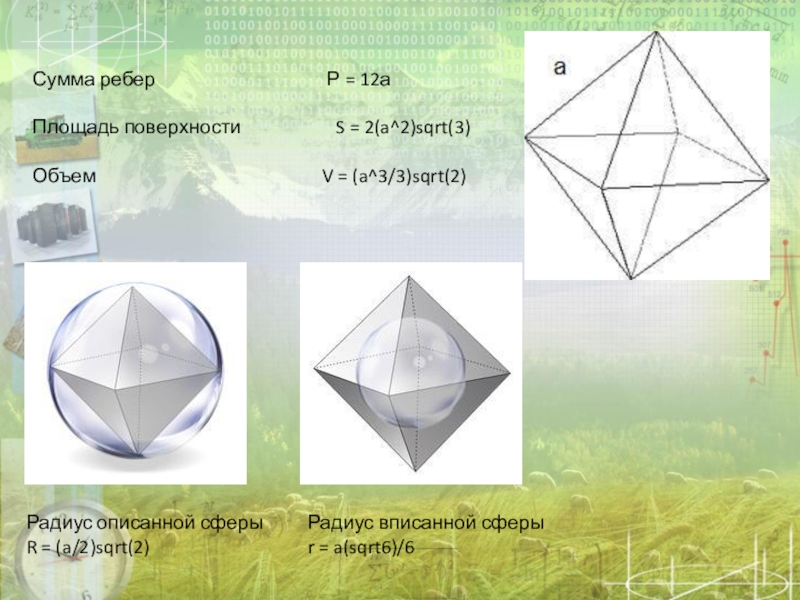
Слайд 3Сумма ребер
Площадь поверхности S = 2(a^2)sqrt(3)
Объем V = (a^3/3)sqrt(2)
Радиус описанной сферы R = (a/2)sqrt(2)
Радиус вписанной сферы r = a(sqrt6)/6
Слайд 4 Свойства
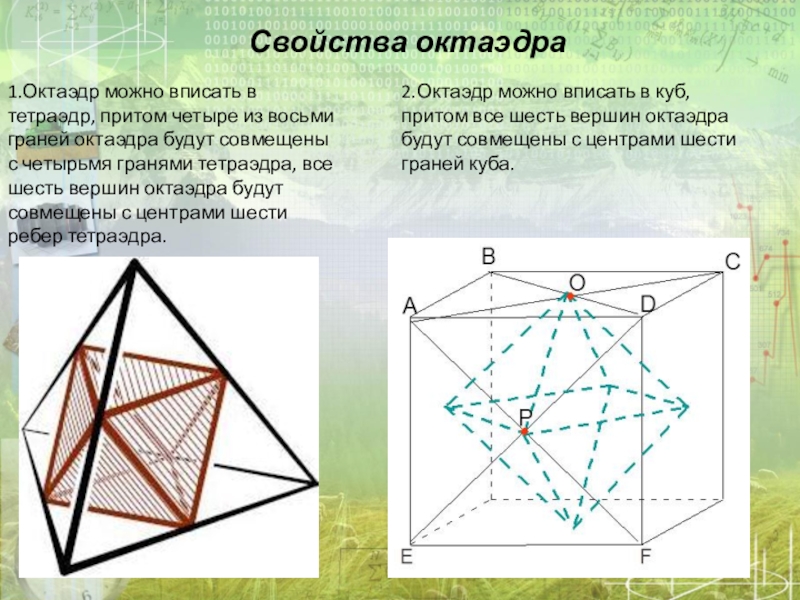
1.Октаэдр можно вписать в тетраэдр, притом четыре из восьми граней октаэдра будут совмещены с четырьмя гранями тетраэдра, все шесть вершин октаэдра будут совмещены с центрами шести ребер тетраэдра.
2.Октаэдр можно вписать в куб, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
Слайд 53.В октаэдр можно вписать куб, притом все восемь вершин куба будут
Слайд 6 Примеры решения задач
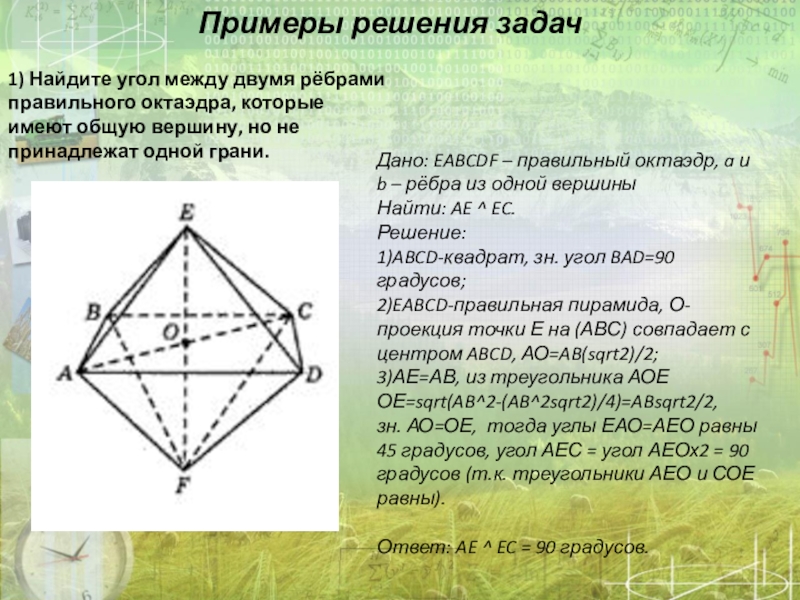
1) Найдите
Дано: EABCDF – правильный октаэдр, a и b – рёбра из одной вершины
Найти: AE ^ EC.
Решение:
1)ABCD-квадрат, зн. угол BAD=90 градусов;
2)EABCD-правильная пирамида, О-проекция точки Е на (АВС) совпадает с центром ABCD, АО=AB(sqrt2)/2;
3)АЕ=АВ, из треугольника АОЕ ОЕ=sqrt(AB^2-(AB^2sqrt2)/4)=ABsqrt2/2,
зн. АО=ОЕ, тогда углы ЕАО=АЕО равны 45 градусов, угол АЕС = угол АЕОх2 = 90 градусов (т.к. треугольники АЕО и СОЕ равны).
Ответ: AE ^ EC = 90 градусов.
Слайд 7 Октаэдр является одним из пяти платоновых тел.
Правильные многогранники называют Платоновыми
Платон считал, что мир строится из четырёх «стихий»: огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников.
Тетраэдр олицетворял огонь; икосаэдр –воду; куб– землю, а октаэдр – воздух. В наше время эту систему можно сравнить с четырьмя состояниями вещества: твёрдым, жидким, газообразным и пламенным. Это была одна из первых попыток ввести в науку идею систематизации.
Слайд 8Немецкий математик и астроном Иоганн Кеплер (1571 – 1630) предположил, что
Согласно этой теории, вокруг сферы Меркурия описан октаэдр. Этот октаэдр вписан в сферу Венеры, вокруг которой описан икосаэдр. Вокруг икосаэдра описана сфера Земли, а вокруг этой сферы - додекаэдр. Додекаэдр вписан в сферу Марса, вокруг которой описан тетраэдр. Вокруг тетраэдра описана сфера Юпитера, вписанная в куб. Наконец, вокруг куба описана сфера Сатурна.
Теория Кеплера
Слайд 9Кубок Кеплера
Год за годом он уточнял свои наблюдения, но наконец отказался
Идеи Кеплера оказались ошибочными, но без гипотез не может существовать наука.
Слайд 10 Интересные факты
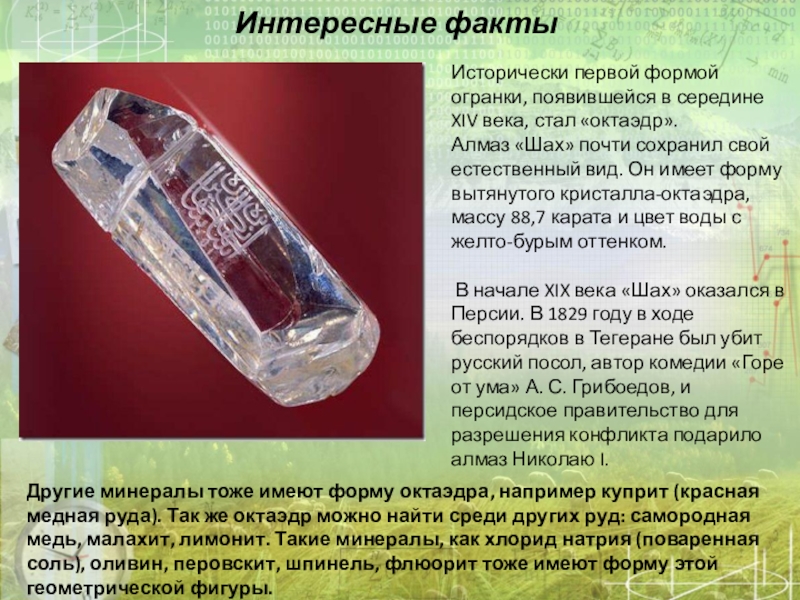
Исторически
Алмаз «Шах» почти сохранил свой естественный вид. Он имеет форму вытянутого кристалла-октаэдра, массу 88,7 карата и цвет воды с желто-бурым оттенком.
В начале XIX века «Шах» оказался в Персии. В 1829 году в ходе беспорядков в Тегеране был убит русский посол, автор комедии «Горе от ума» А. С. Грибоедов, и персидское правительство для разрешения конфликта подарило алмаз Николаю I.
Другие минералы тоже имеют форму октаэдра, например куприт (красная медная руда). Так же октаэдр можно найти среди других руд: самородная медь, малахит, лимонит. Такие минералы, как хлорид натрия (поваренная соль), оливин, перовскит, шпинель, флюорит тоже имеют форму этой геометрической фигуры.
Слайд 121)Монокристаллы алюмокалиевых квасцов имеют форму октаэдра. Они применяются для протравливания тканей,
2)Леонардо да Винчи открыл звёздчатый октаэдр. Его можно рассматривать, как соединение двух тетраэдров. Сто лет спустя звездчатый октаэдр был заново открыт Иоганном Кеплером, который назвал его звезда восьмиугольная.
Слайд 14Из каких фигур составлен октаэдр?
Из равносторонних треугольников.
Сколько граней имеет октаэдр?
Сколько рёбер
Сколько вершин у октаэдра?
8 граней.
12 рёбер.
6 вершин.
Задача.
Ребро правильного октаэдра равно а. Найдите расстояние между: а) двумя его противоположными вершинами;
б) центрами двух смежных граней;
в) противоположными гранями.
Ответ: а) (sqrt2)a ; б) a(sqrt2)/3; в) a(sqrt6)/3.