- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Объем прямой призмы (11 класс)
Содержание
- 1. Презентация по геометрии Объем прямой призмы (11 класс)
- 2. Если будем знать объем прямой призмы, в
- 3. Теорема: Объем прямой призмы равен произведению
- 4. Провести такую высоту треугольника АВС, которая разделяет
- 5. Рассмотрите доказательство теоремы, приведенное в учебнике.Доказать:V =
- 6. Теорема: Объем прямой призмы равен произведению
- 7. S1S2S3Эту призму можно разбить на прямые треугольные
- 8. Рассмотрите доказательство этой части теоремы, приведенное в
- 9. Доказательство:Доказать:V = S · hОформите доказательство двух частей теоремы.
- 10. Что нужно знать для нахождения объема прямой
Слайд 2Если будем знать объем прямой призмы, в осно-вании которой лежит произвольный
Объем каких геометрических тел
мы уже знаем, как вычислить?
Объем какого тела можно будет вывести, опираясь на изученное?
Куба; прямоугольного параллелепипеда;
прямой призмы, основанием которой является прямоугольный треугольник.
Объем прямой призмы, основанием которой является произвольный треугольник.
Объем любой прямой призмы.
Итак, докажем 2 части теоремы об объеме прямой призмы
Слайд 3
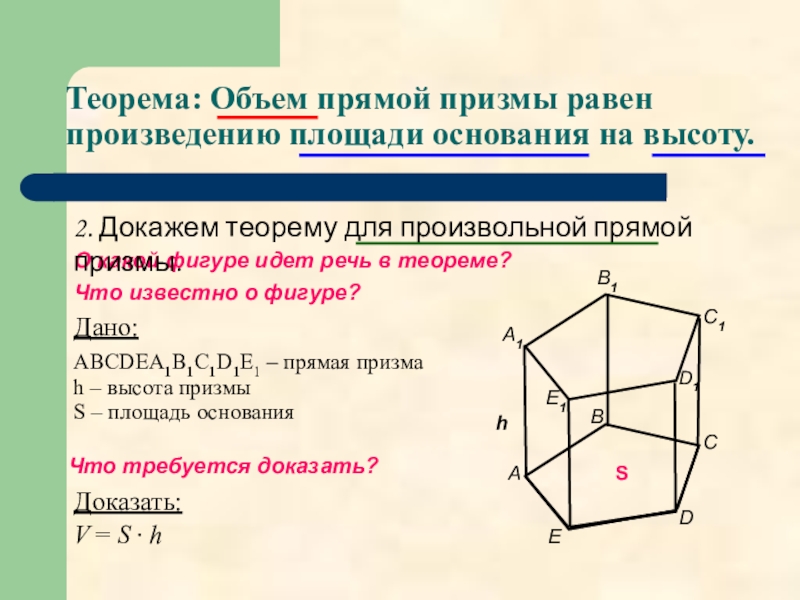
Теорема: Объем прямой призмы равен
произведению площади основания на высоту.
О какой фигуре
Что известно о фигуре?
1. Докажем теорему для треугольной прямой призмы.
Дано:
ABCA1B1C1 – прямая призма
Доказать:
V = SABC · h
h – высота призмы
h
Что требуется доказать?
S – площадь основания
S
Слайд 4Провести такую высоту треугольника АВС, которая разделяет этот треугольник на 2
D
D1
Плоскость BB1D разделяет данную призму на 2 призмы.
Поэтому объемы V1 и V2 этих призм можно найти :
V1 = SABD · h и V2 = SBDC · h.
По свойству объемов V = V1 + V2 , т.е.
V = SABD · h + SBDC · h = (SABD + SBDC) · h
V = SABC · h
Основаниями призм являются прямоугольные
треугольники: ABD
и BDC.
Какие приемы сведения к известным фигурам использовались при выводе формул площади?
Доказать: V = SABC · h
Какие могут использоваться при выводе
формулы объема данной призмы?
Дополнение.
Разбиение.
Какое разбиение провести?
Поможет ли это разбиение?
Слайд 5Рассмотрите доказательство теоремы, приведенное в учебнике.
Доказать:
V = SABC · h
Выделите этапы
1).
2).
3).
Какой прием сведения к известным телам использовался?
Слайд 6
Теорема: Объем прямой призмы равен
произведению площади основания на высоту.
О какой фигуре
Что известно о фигуре?
2. Докажем теорему для произвольной прямой призмы.
Дано:
ABCDЕA1B1C1D1Е1 – прямая призма
Доказать:
V = S · h
h – высота призмы
h
Что требуется доказать?
S – площадь основания
S
Слайд 7
S1
S2
S3
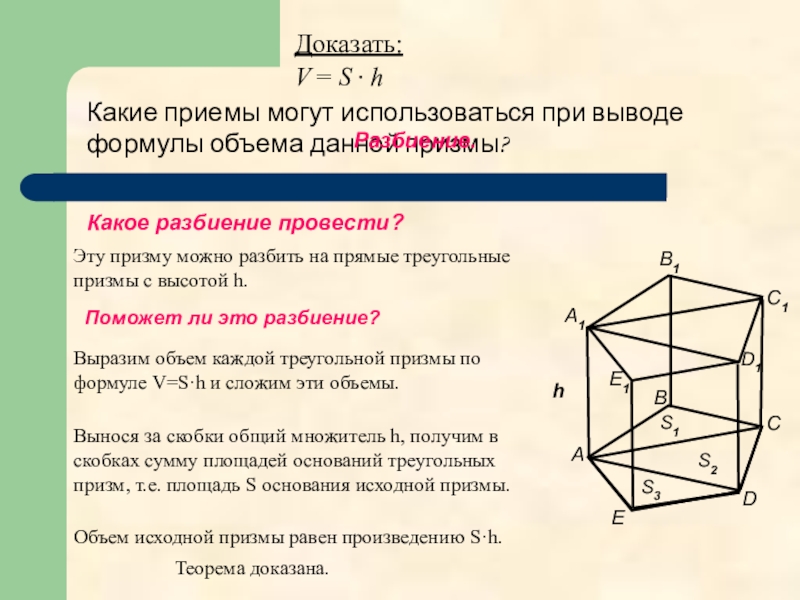
Эту призму можно разбить на прямые треугольные призмы с высотой h.
Выразим
Вынося за скобки общий множитель h, получим в скобках сумму площадей оснований треугольных призм, т.е. площадь S основания исходной призмы.
Объем исходной призмы равен произведению S·h.
Теорема доказана.
Доказать:
V = S · h
Какие приемы могут использоваться при выводе формулы объема данной призмы?
Разбиение.
Какое разбиение провести?
Поможет ли это разбиение?
h
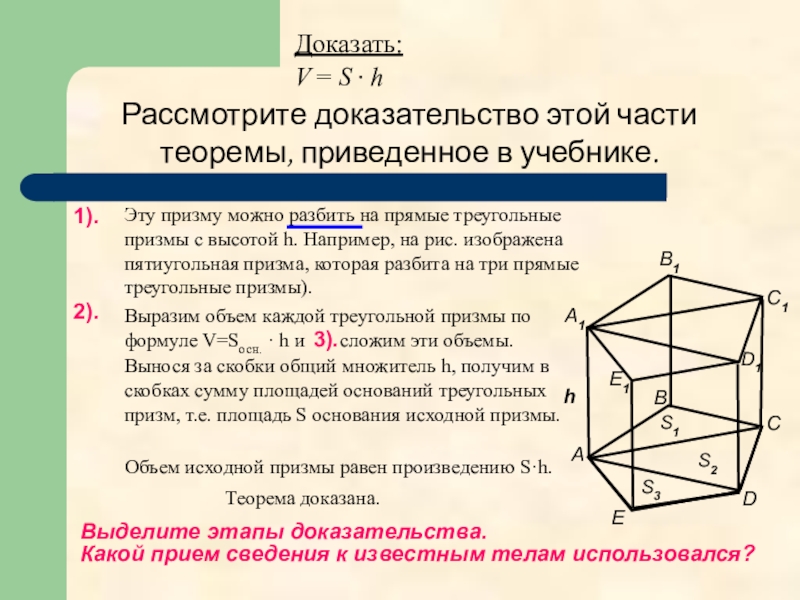
Слайд 8Рассмотрите доказательство этой части теоремы, приведенное в учебнике.
Доказать:
V = S ·
Выделите этапы доказательства.
Какой прием сведения к известным телам использовался?
1).
2).
3).
h
Слайд 10Что нужно знать для нахождения объема прямой призмы?
Высоту призмы и площадь
Как найти объем такой призмы, зная эти данные?
Перемножить площадь основания призмы на высоту призмы,
т.е. по формуле V = S · h.
Объем прямой призмы
Что нужно знать для нахождения объема прямой треугольной призмы, если не будет известна площадь основания?
Любые данные о треугольнике, лежащем в основании, по которым можно вычислить площадь треугольника.
Приведите примеры
Какие приемы использовались при доказательстве теоремы?
1) Выделение 2-х случаев (треугольная, произвольная прямая призма).
2) Разбиение данной призмы на такие, чей объем можно вычислить.