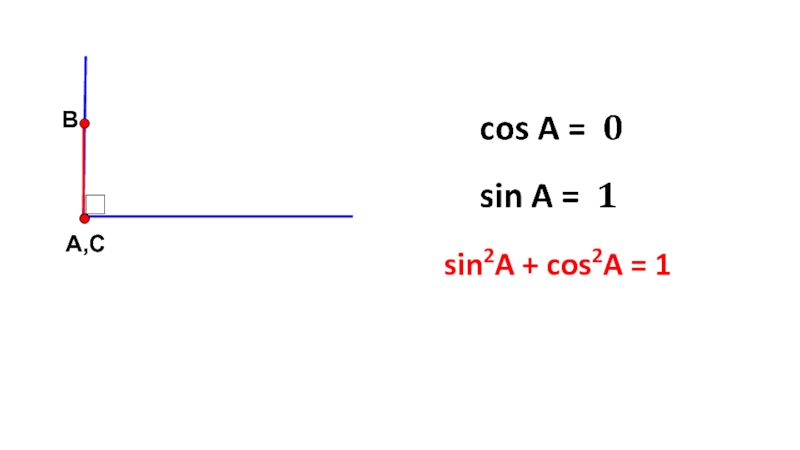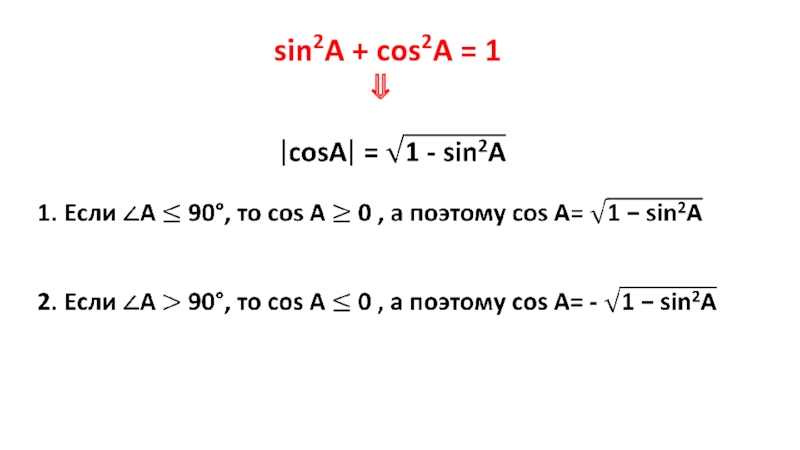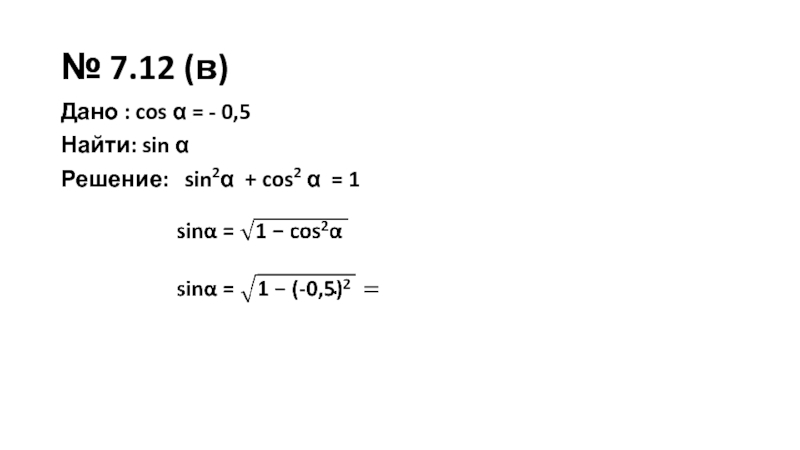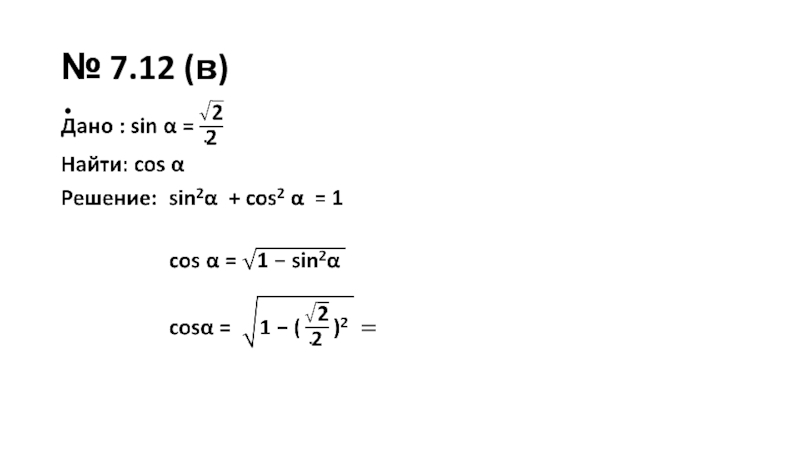- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на темуОсновное тригонометрическое тождество (8 класс)
Содержание
- 1. Презентация по геометрии на темуОсновное тригонометрическое тождество (8 класс)
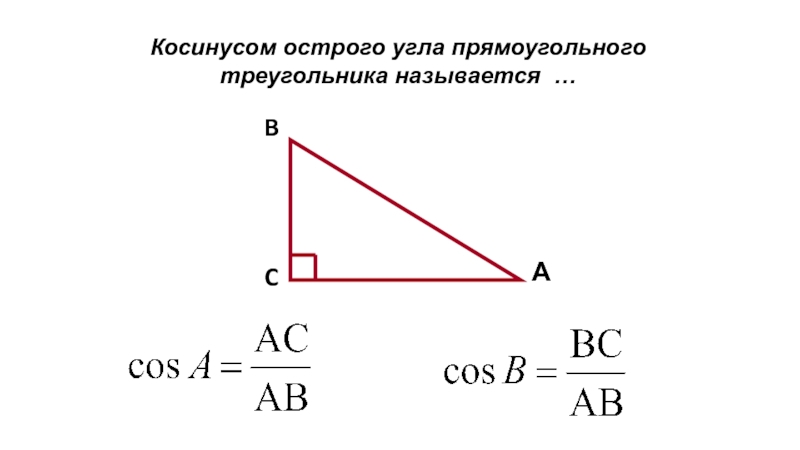
- 2. Косинусом острого угла прямоугольного треугольника называется …
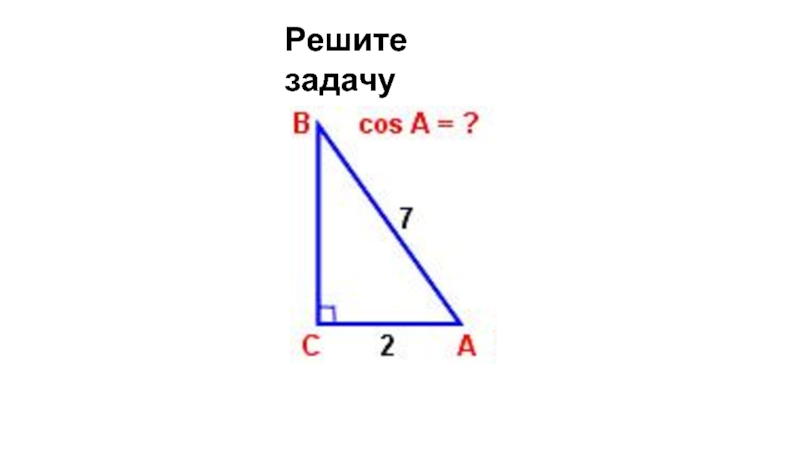
- 3. Решите задачу
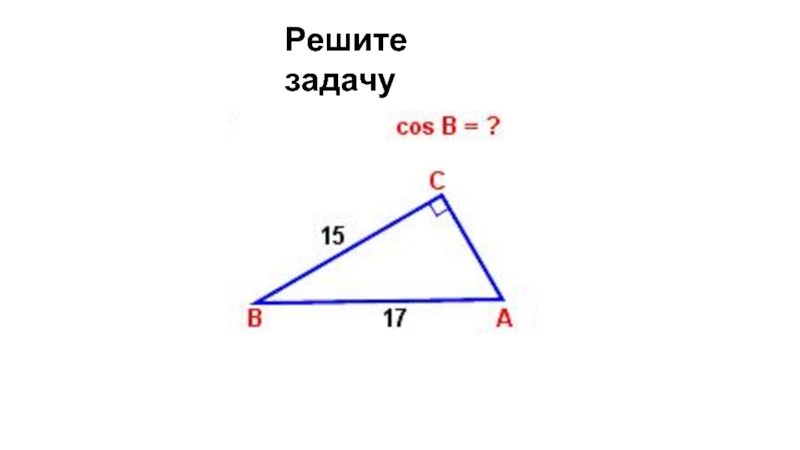
- 4. Решите задачу
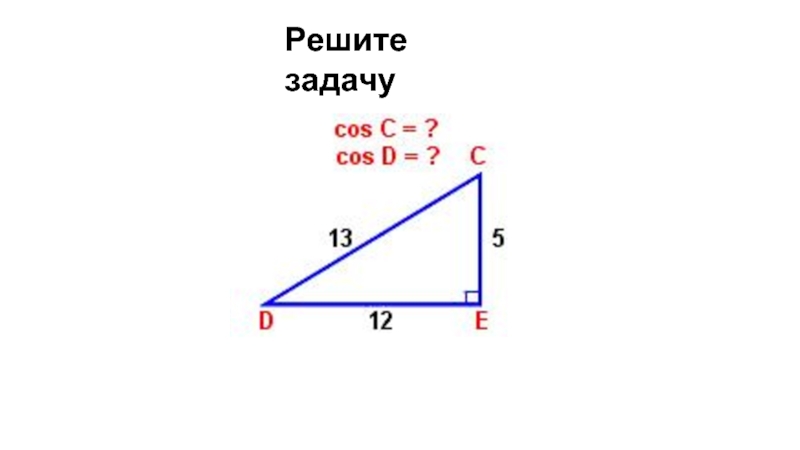
- 5. Решите задачу
- 6. Основное тригонометрическое тождество 30. 03. 18 Классная работаsin2A + cos2A = 1
- 7. sin2A + cos2A = 1ТогдаПо теореме Пифагора Поэтому иBAC
- 8. ABCsin2A + cos2A = 1
- 9. ВА,Сsin2A + cos2A = 1
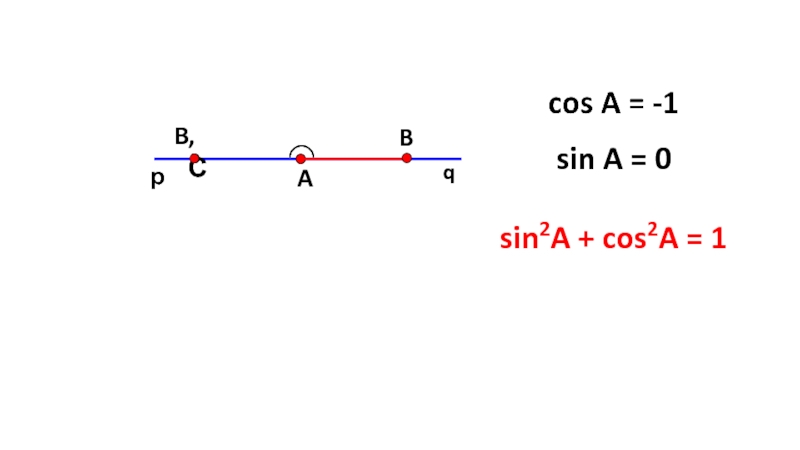
- 10. ◠рqAsin A = 0sin2A + cos2A = 1B
- 11. sin2A + cos2A = 1 ⇓
- 12. Зависимость между косинусом смежных углов теперь можно записать так:cos(180° - α) = - cos α
- 13. № 7. 10Найдите косинусы следующих углов:а) 0°
- 14. № 7.12 (в)Дано : cos α =
- 15. № 7.12 (в)
- 16. Домашнее заданиеn 7.2№ 7. 11, № 7.
Косинусом острого угла прямоугольного треугольника называется …
Слайд 13№ 7. 10
Найдите косинусы следующих углов:
а) 0° , б) 30 °
, в) 45 ° , г) 60 ° , д) 90 ° , е) 120 ° , ж) 135 ° , з) 150 ° , и) 180 ° .