:
«Высота, медиана, биссектриса»
учителя математики
ГБОУ школы №1056
Романенко Елены Алексеевны
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Высота, медиана, биссектриса
Содержание
- 1. Презентация по геометрии на тему Высота, медиана, биссектриса
- 2. Высота треугольника -перпендикуляр, проведенный из вершины треугольника
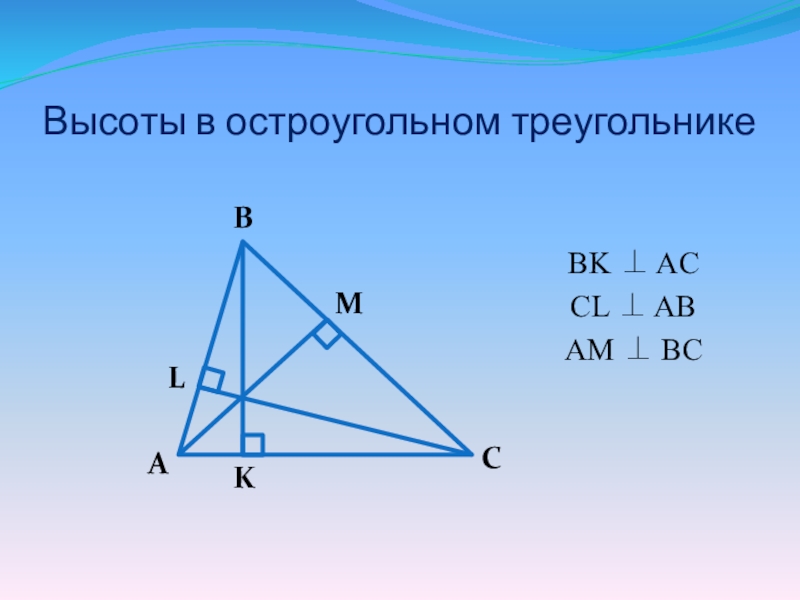
- 3. Высоты в остроугольном треугольникеBK ACCL ABAM BC
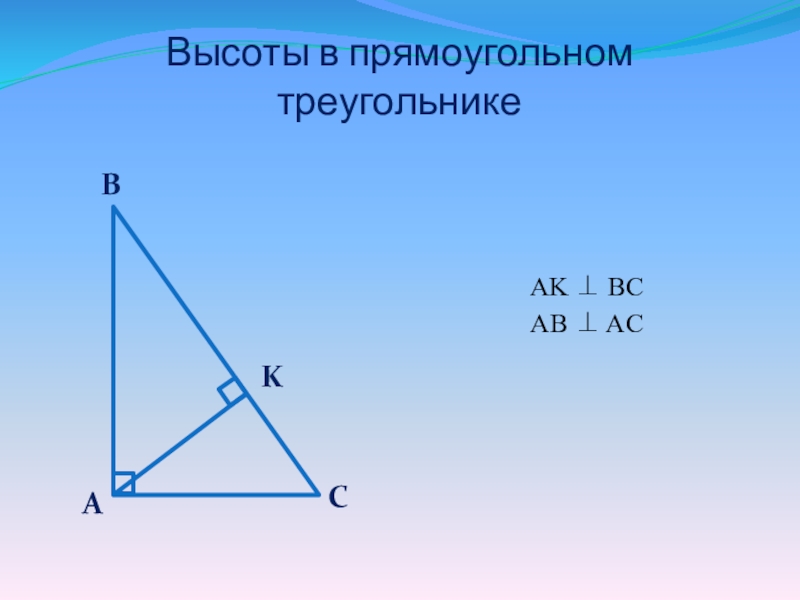
- 4. Высоты в прямоугольном треугольникеAK BCAB AC
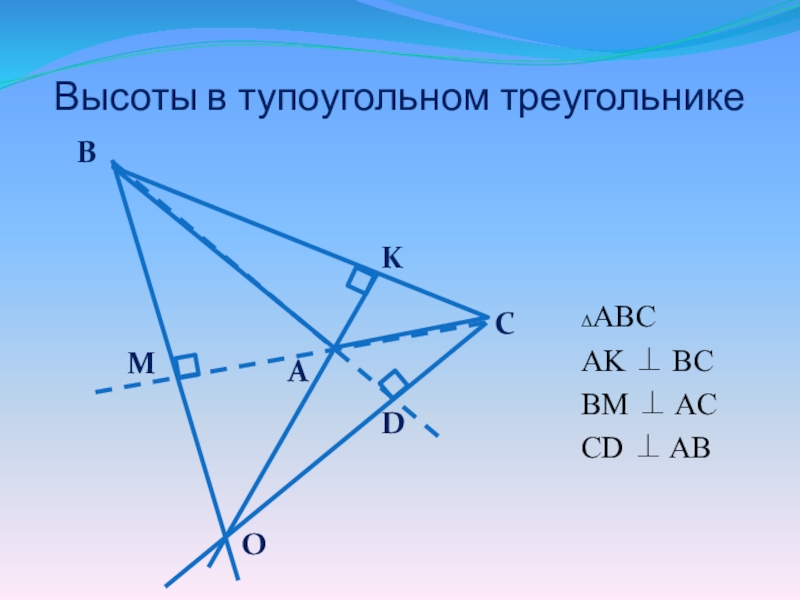
- 5. Высоты в тупоугольном треугольникеΔABCAK BCBM ACCD ABABCKDMО
- 6. Биссектриса треугольника - Биссектрисой треугольника, проведенной из
- 7. Биссектрисы в остроугольном треугольнике
- 8. Биссектрисы в прямоугольном треугольникеBK – биссектриса AM
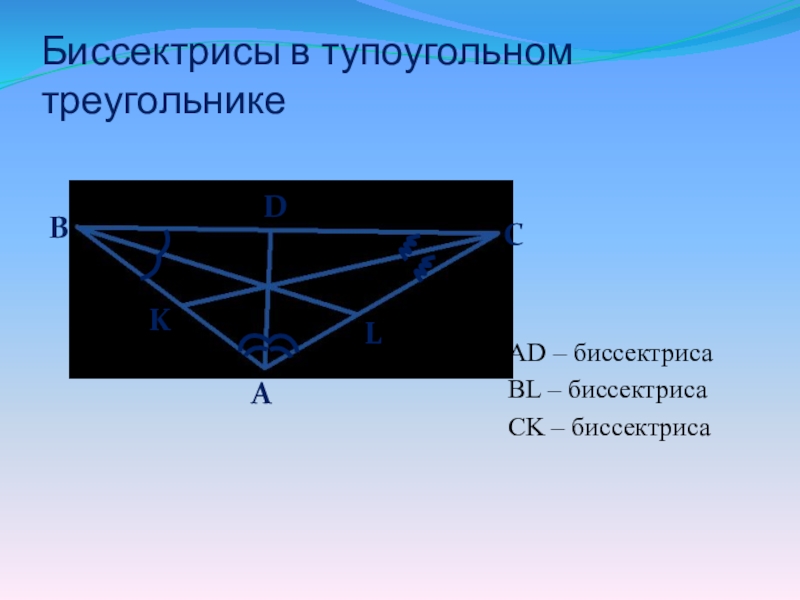
- 9. Биссектрисы в тупоугольном треугольникеAD – биссектриса BL – биссектриса CK – биссектриса
- 10. Свойство биссектрисы треугольника
- 11. Биссектриса треугольника делит противолежащую сторону на отрезки,
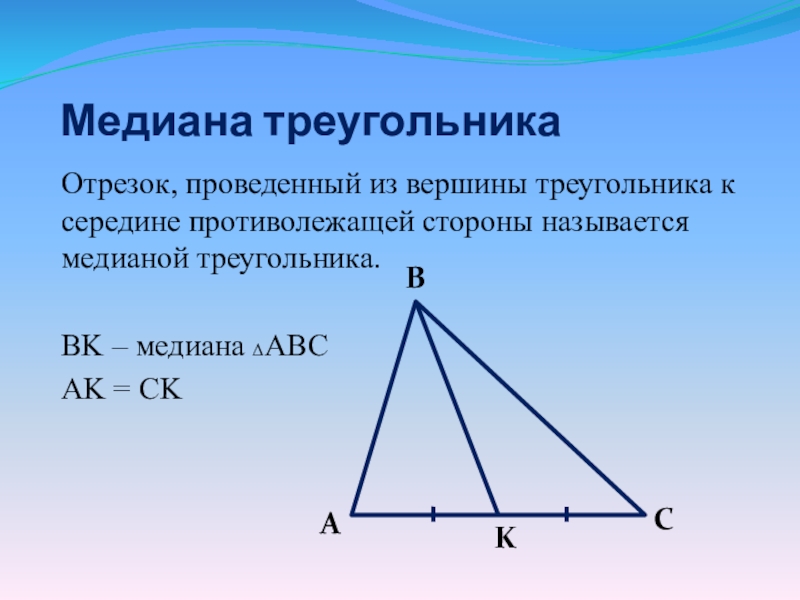
- 12. Медиана треугольникаОтрезок, проведенный из вершины треугольника к
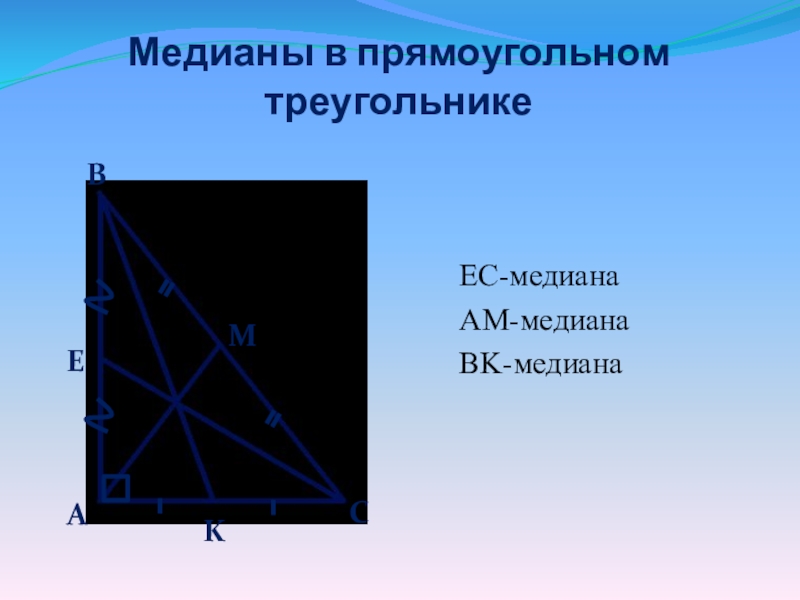
- 13. Медианы в прямоугольном треугольникеEC-медиана
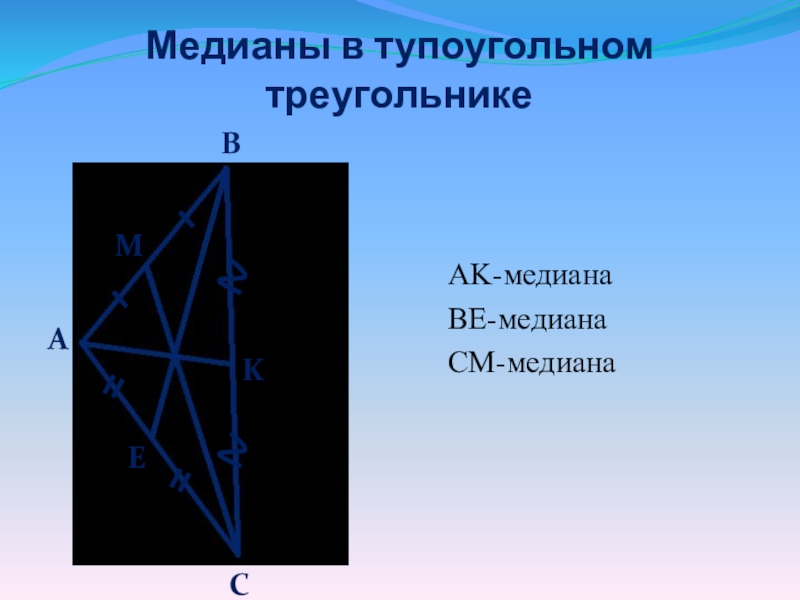
- 14. Медианы в тупоугольном треугольникеAK-медианаBE-медианаCM-медианаСEAMBK
- 15. Свойство медиан треугольника
- 16. Медианы в треугольнике пересекаются в одной точке
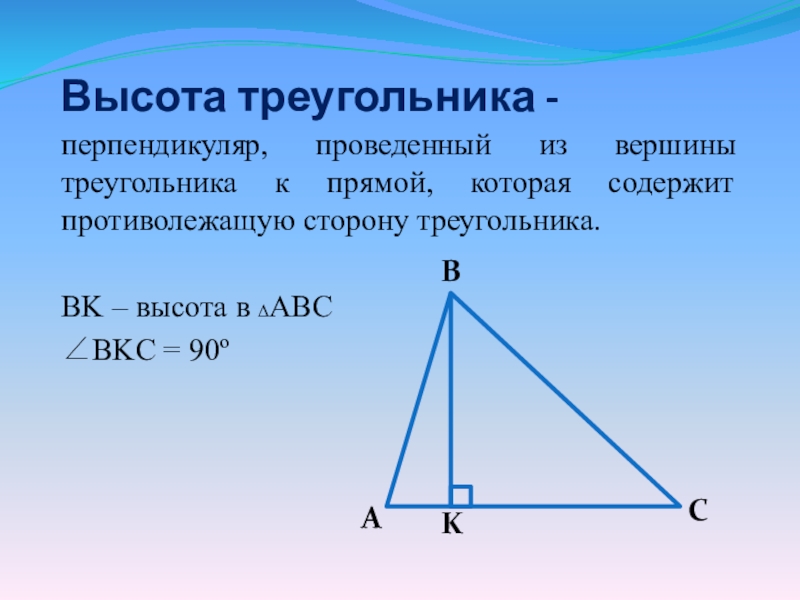
Высота треугольника -перпендикуляр, проведенный из вершины треугольника к прямой, которая содержит противолежащую сторону треугольника.BK – высота в ΔABC BKC = 90º
Слайд 1Департамент образования города Москвы
Северо-Западное окружное управление образования
Презентация по геометрии на тему
Слайд 2Высота треугольника -
перпендикуляр, проведенный из вершины треугольника к прямой, которая содержит
противолежащую сторону треугольника.
BK – высота в ΔABC
BKC = 90º
BK – высота в ΔABC
BKC = 90º
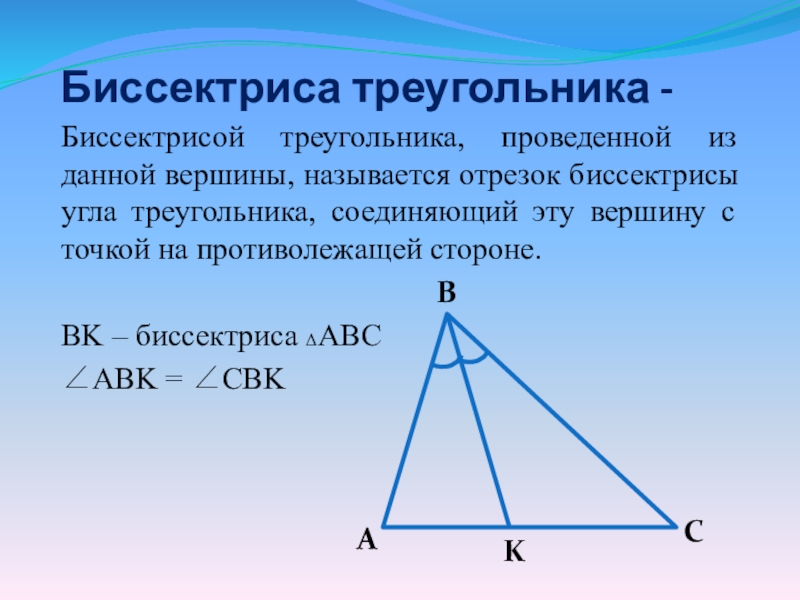
Слайд 6Биссектриса треугольника -
Биссектрисой треугольника, проведенной из данной вершины, называется отрезок
биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне.
BK – биссектриса ΔABC
ABK = CBK
BK – биссектриса ΔABC
ABK = CBK
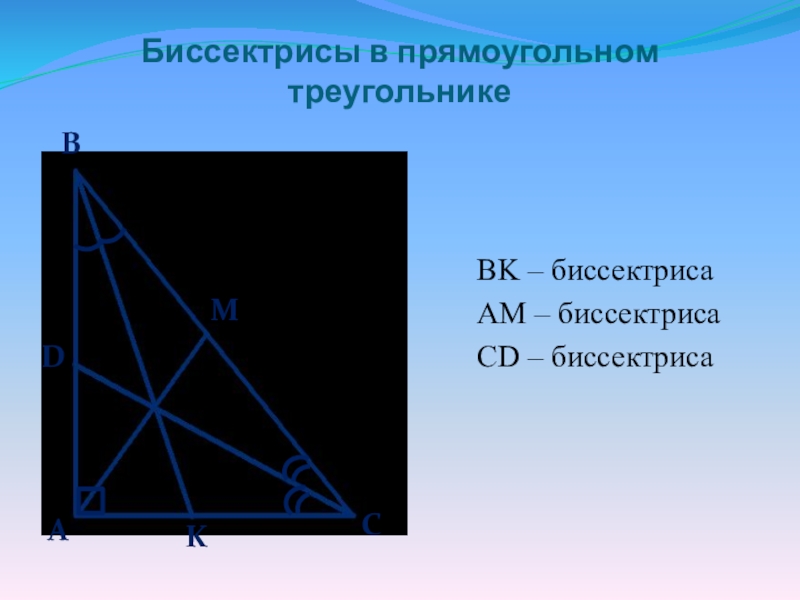
Слайд 8Биссектрисы в прямоугольном треугольнике
BK – биссектриса
AM – биссектриса
CD – биссектриса
A
D
B
M
C
K
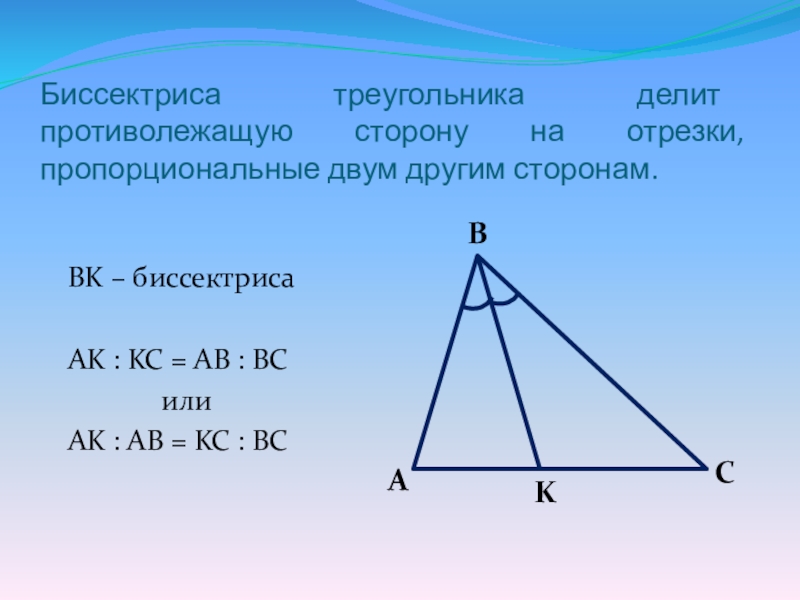
Слайд 11Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам.
BK
– биссектриса
AK : KC = AB : BC
или
AK : AB = KC : BC
AK : KC = AB : BC
или
AK : AB = KC : BC
Слайд 12Медиана треугольника
Отрезок, проведенный из вершины треугольника к середине противолежащей стороны называется
медианой треугольника.
BK – медиана ΔABC
AK = CK
BK – медиана ΔABC
AK = CK
Слайд 16Медианы в треугольнике пересекаются в одной точке и точкой пересечения делятся
в отношении 2:1, считая от вершины.
BK – медиана
AM – медиана
CL – медиана
BO : OK = 2:1
AO : OM = 2:1
CO : OL = 2:1
О