П.Кунчур
2018 г
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Вписанный угол 8 класс
Содержание
- 1. Презентация по геометрии на тему Вписанный угол 8 класс
- 2. 1 вариантДуга называется _________________________ , если отрезок,
- 3. Ответы к тесту на повторение2 вариант.1.центральный.2.центрального угла.3.г4.г
- 4. Практическая работа по выявлению понятия вписанного угла.1.Сделать
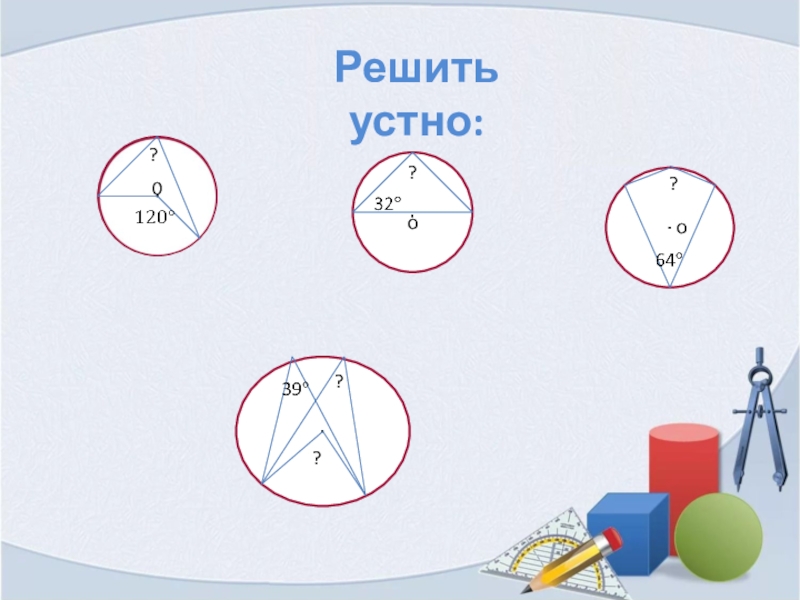
- 5. ?Решить устно: ??0оо??
- 6. Продолжаем практическую работу измеряем , сравниваем различными способами вписанный и центральный углыи выдвигаем гипотезу.Вывод:
- 7. 1.Градусная мера вписанного угла равна 140 °.
- 8. Ответы к задачам.1.б)2.б)3.а)4.а)5.в)
- 9. Я вас люблю!Спасибо за урок
1 вариантДуга называется _________________________ , если отрезок, соединяющий ее концы, является диаметром окружности.Если дуга окружности больше полуокружности, то ее градусная мера считается равной _____________________________________.Чему равен центральный угол, если дуга, на которую он опирается, равна 700?
Слайд 21 вариант
Дуга называется _________________________ , если отрезок, соединяющий ее концы, является
диаметром окружности.
Если дуга окружности больше полуокружности, то ее градусная мера считается равной _____________________________________.
Чему равен центральный угол, если дуга, на которую он опирается, равна 700? а) 350 б) 700 в) 1400 г) 2900
Определить градусную меру дуги окружности, если градусная мера соответствующего ему центрального угла равна 40 ° .
а) 40° б) 20° в) 140° г) 80°
Если дуга окружности больше полуокружности, то ее градусная мера считается равной _____________________________________.
Чему равен центральный угол, если дуга, на которую он опирается, равна 700? а) 350 б) 700 в) 1400 г) 2900
Определить градусную меру дуги окружности, если градусная мера соответствующего ему центрального угла равна 40 ° .
а) 40° б) 20° в) 140° г) 80°
2 вариант
Угол с вершиной в центре окружности называется ___________________________
Если дуга окружности меньше полуокружности или является полуокружностью, то ее градусная мера считается равной градусной мере ________________________________________________.
Чему равен центральный угол, если дуга, на которую он опирается, равна 500?
а) 250 б) 1000 в) 3100 г) 500
Определить градусную меру дуги окружности, если градусная мера соответствующего ему центрального угла равна 80 ° .
а) 40° б) 20° в) 140° г) 80°
Слайд 4Практическая работа по выявлению понятия
вписанного угла.
1.Сделать макет круга , отметить
центр
2.Приклеить центральный угол.
3.Выбрать произвольную точку в круге(рассмотреть
все возможные случаи).
4. Выбрать точку на окружности.
5.С вершиной в этой точке построить угол.
Вывод: определение вписанного угла
2.Приклеить центральный угол.
3.Выбрать произвольную точку в круге(рассмотреть
все возможные случаи).
4. Выбрать точку на окружности.
5.С вершиной в этой точке построить угол.
Вывод: определение вписанного угла
Слайд 6Продолжаем практическую работу измеряем ,
сравниваем различными способами
вписанный и
центральный углы
и выдвигаем гипотезу.
Вывод:
и выдвигаем гипотезу.
Вывод:
Слайд 71.Градусная мера вписанного угла равна 140 °. Определить градусную меру дуги,
на которую он опирается.
а) 100° б) 70° в) 280° г) 140°
2.Градусная мера дуги, на которую опирается вписанный угол, равна 90°. Определить градусную меру этого вписанного угла.
а) 100° б) 45° в) 180° г) 90°
3.Определить градусную меру угла, вписанного в окружность, если соответствующий ему центральный угол равен 126 ° .
а) 63° б) 252° в) 180° г) 126°
а) 100° б) 70° в) 280° г) 140°
2.Градусная мера дуги, на которую опирается вписанный угол, равна 90°. Определить градусную меру этого вписанного угла.
а) 100° б) 45° в) 180° г) 90°
3.Определить градусную меру угла, вписанного в окружность, если соответствующий ему центральный угол равен 126 ° .
а) 63° б) 252° в) 180° г) 126°
4. Хорда делит окружность в отношении 5:13. Определить величины вписанных углов, опирающихся на эту хорду.
а) 50° и 130 ° б) 100° и 260 ° в) 25° и 60 ° г) 120° и 240 °
5.Вершины треугольника АВС делят окружность в отношении 2:3:4. Найти углы этого треугольника.
а) 60 °, 70 ° ,50 ° б) 40°, 90°, 50° в) 40 °, 60 °, 80 °
Решаем в парах:
