- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Возникновение понятия Пирамида
Содержание
- 1. Презентация по геометрии на тему Возникновение понятия Пирамида
- 2. НЕМНОГО ИСТОРИИ«Пирамида» - от греческого слова «пюрамис»,
- 3. ПИРАМИДЫ В АРХИТЕКТУРЕНовый вход в Лувр, ПарижТорговый
- 4. Понятие пирамиды• А1А2А3 … Аn - основание•
- 5. Площадь пирамиды Площадью полной поверхности пирамиды
- 6. Понятие правильной пирамидыМАВСDЕF - правильнаяпирамида, еслиАВСDЕF –
- 7. Треугольная правильная пирамидаABC – правильный;О – точка пересечения медиан (высоти биссектрис),центр вписаннойи описаннойокружностей.
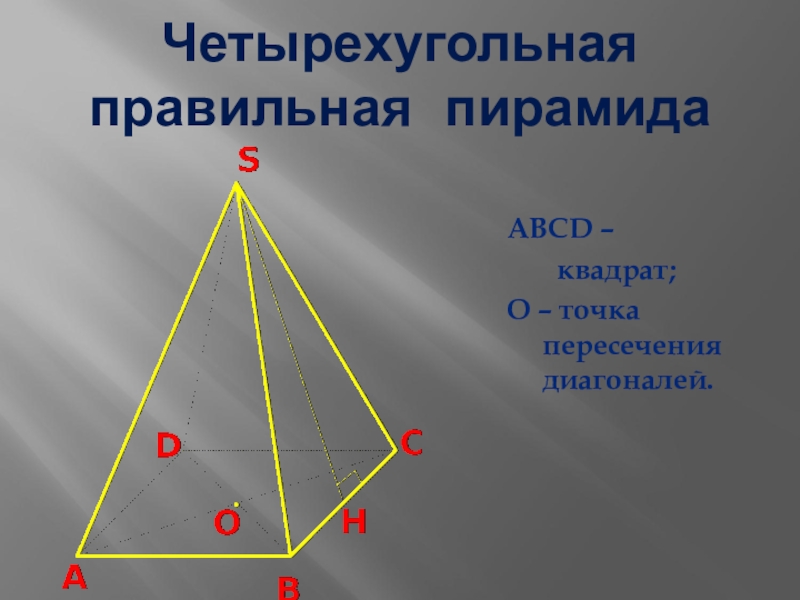
- 8. Четырехугольная правильная пирамидаABCD – квадрат;О – точка пересечения диагоналей.
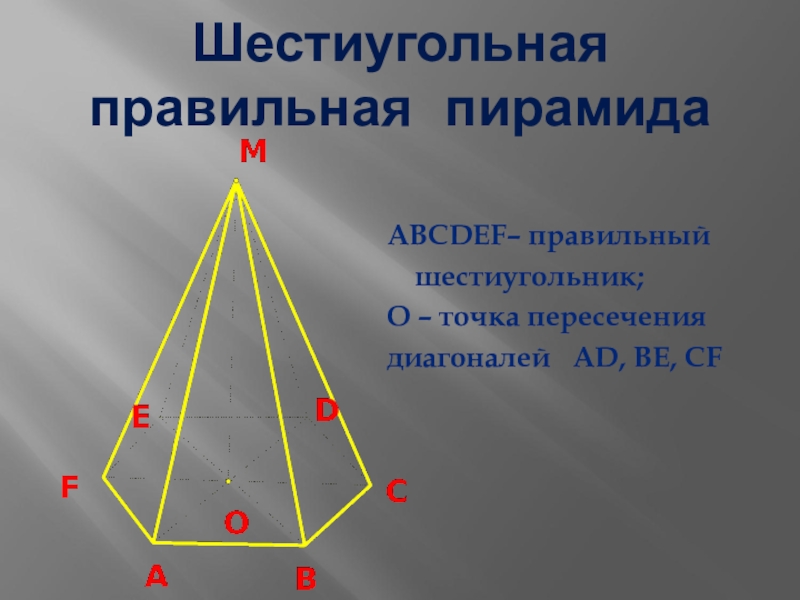
- 9. Шестиугольная правильная пирамидаABCDЕF– правильный шестиугольник;О – точка пересечениядиагоналей AD, BE, CF
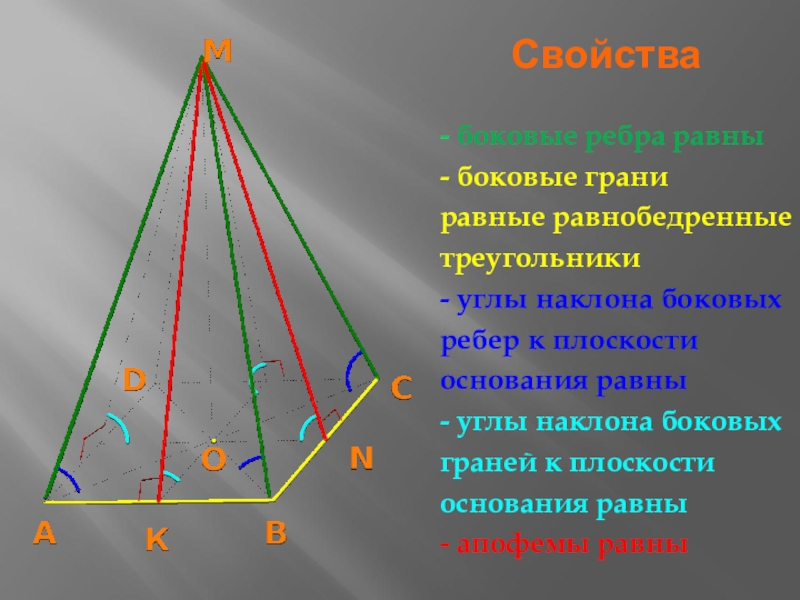
- 10. Свойства- боковые ребра равны- боковые граниравные равнобедренныетреугольники-
- 11. ТеоремаПлощадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
- 12. ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПРАВИЛЬНОЙ ПИРАМИДЫSбок. = Pосн.
- 13. ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ПИРАМИДЫSполн. = Sбок. + Sосн. где Sосн. – площадь основания.
- 14. ОБЪЁМ ПИРАМИДЫV = Sосн. * hгде Sосн. – площадь основания, h – высота пирамиды.
НЕМНОГО ИСТОРИИ«Пирамида» - от греческого слова «пюрамис», которым греки называли египетские пирамиды.Мексиканская пирамида СолнцаЕгипетские пирамидыГора Кайлас на Тибете
Слайд 2НЕМНОГО ИСТОРИИ
«Пирамида» - от греческого
слова «пюрамис», которым
греки называли египетские
пирамиды.
Мексиканская пирамида Солнца
Египетские пирамиды
Гора Кайлас на Тибете
Слайд 3ПИРАМИДЫ В АРХИТЕКТУРЕ
Новый вход в Лувр, Париж
Торговый центр в Илинге,
Лондон
Александровский маяк
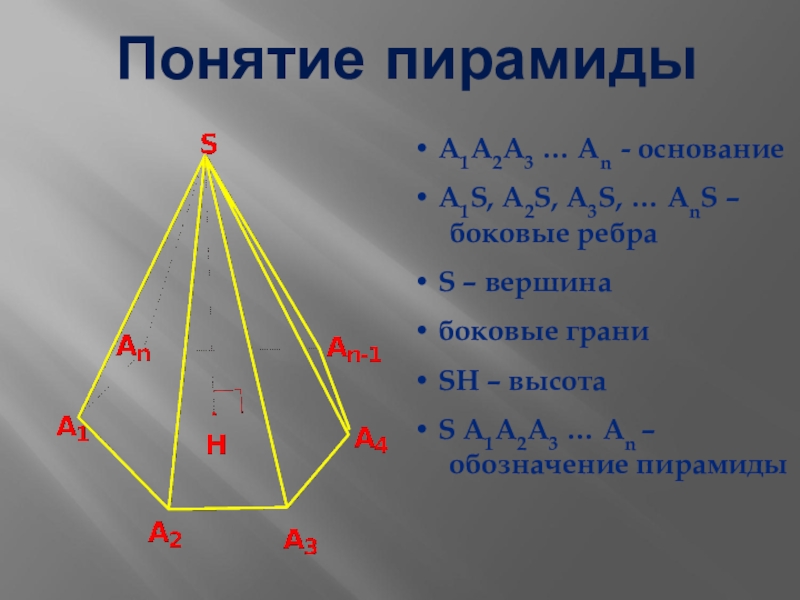
Слайд 4Понятие пирамиды
• А1А2А3 … Аn - основание
• А1S, А2S, А3S, …
АnS – боковые ребра
• S – вершина
• боковые грани
• SH – высота
• S А1А2А3 … Аn – обозначение пирамиды
• S – вершина
• боковые грани
• SH – высота
• S А1А2А3 … Аn – обозначение пирамиды
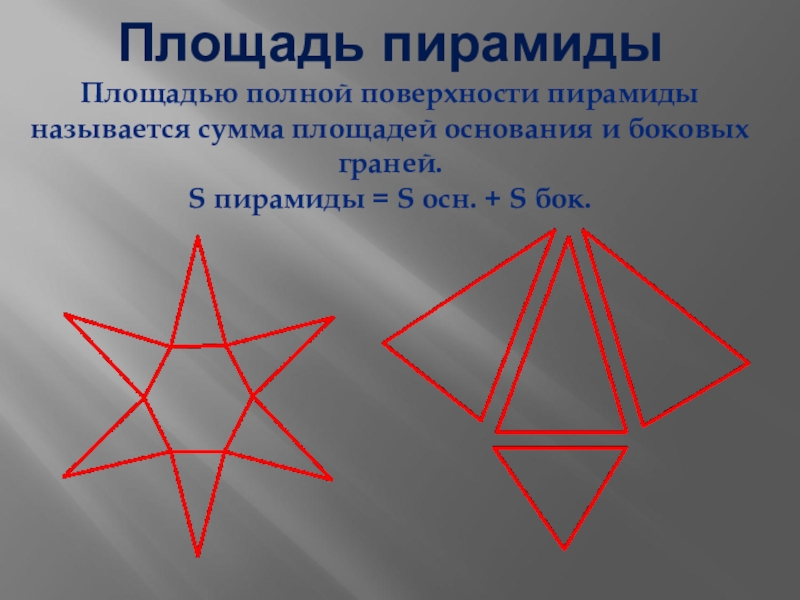
Слайд 5 Площадь пирамиды Площадью полной поверхности пирамиды называется сумма площадей основания и боковых граней. S
пирамиды = S осн. + S бок.
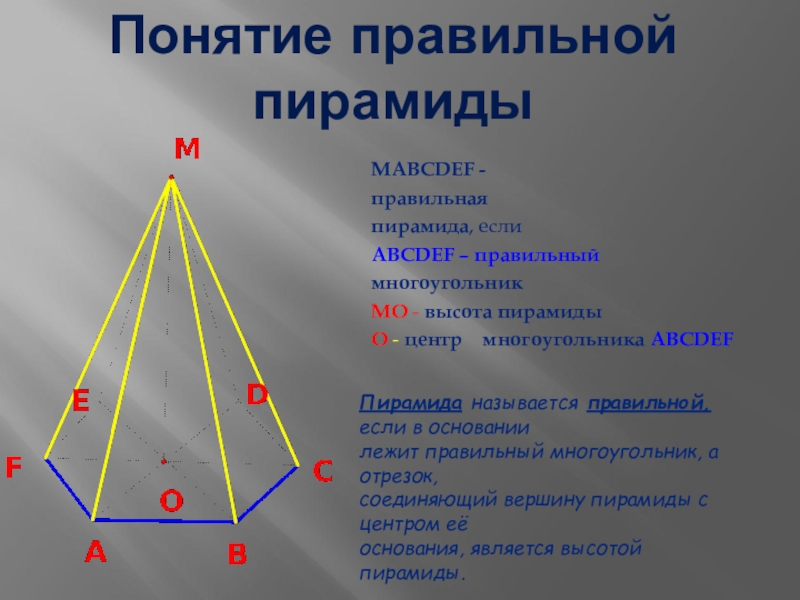
Слайд 6Понятие правильной пирамиды
МАВСDЕF -
правильная
пирамида, если
АВСDЕF – правильный
многоугольник
МО - высота пирамиды
О
- центр многоугольника АВСDЕF
Пирамида называется правильной, если в основании
лежит правильный многоугольник, а отрезок,
соединяющий вершину пирамиды с центром её
основания, является высотой пирамиды.
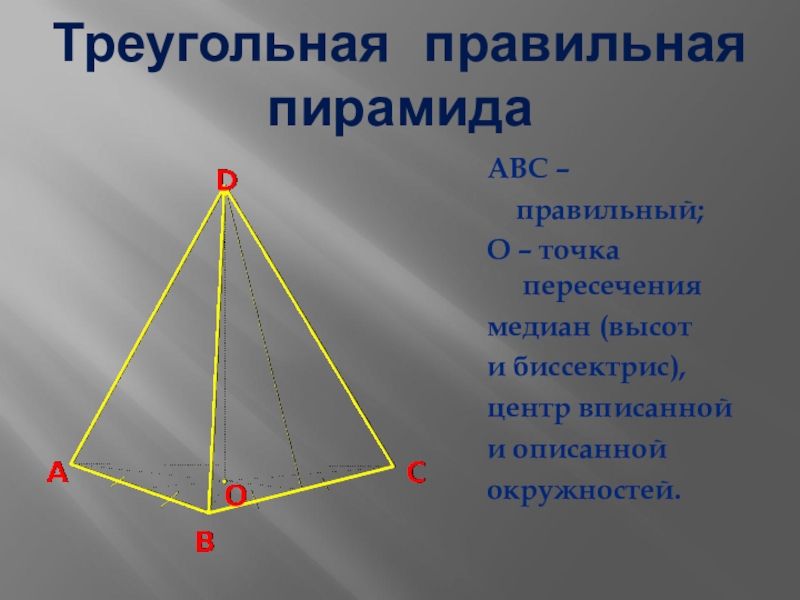
Слайд 7Треугольная правильная пирамида
ABC –
правильный;
О – точка пересечения
медиан
(высот
и биссектрис),
центр вписанной
и описанной
окружностей.
и биссектрис),
центр вписанной
и описанной
окружностей.
Слайд 9Шестиугольная правильная пирамида
ABCDЕF– правильный
шестиугольник;
О – точка пересечения
диагоналей AD, BE,
CF
Слайд 10Свойства
- боковые ребра равны
- боковые грани
равные равнобедренные
треугольники
- углы наклона боковых
ребер к
плоскости
основания равны
- углы наклона боковых
граней к плоскости
основания равны
- апофемы равны
основания равны
- углы наклона боковых
граней к плоскости
основания равны
- апофемы равны
Слайд 11 Теорема
Площадь боковой поверхности правильной пирамиды
равна половине произведения периметра основания
на апофему.
Слайд 12ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПРАВИЛЬНОЙ ПИРАМИДЫ
Sбок. = Pосн. * l
где Pосн. –
периметр основания,
l –апофема правильной пирамиды.
l –апофема правильной пирамиды.