- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Уравнение окружности (9 класс)
Содержание
- 1. Презентация по геометрии на тему Уравнение окружности (9 класс)
- 2. Цели урока:Образовательные: Вывести уравнение окружности, рассмотрев решение
- 3. ПовторениеЗапишите формулу нахождения координат середины отрезка.Запишите формулу
- 4. Повторение:1. Даны точки А ( - 1;
- 5. Повторение:2. Найдите координаты вектора
- 6. Уравнение окружности.1. Дайте определение окружности.2. Что
- 7. 1 этап: Вывод формулыУравнение фигуры – это
- 8. Вывод формулыПусть дана окружность.А(а;b) – центр окружности,
- 9. Формула I(х – а)2 + (у –
- 10. Формула II(х – а)2 + (у –
- 11. Для того чтобы составить уравнение окружности, нужно:1)
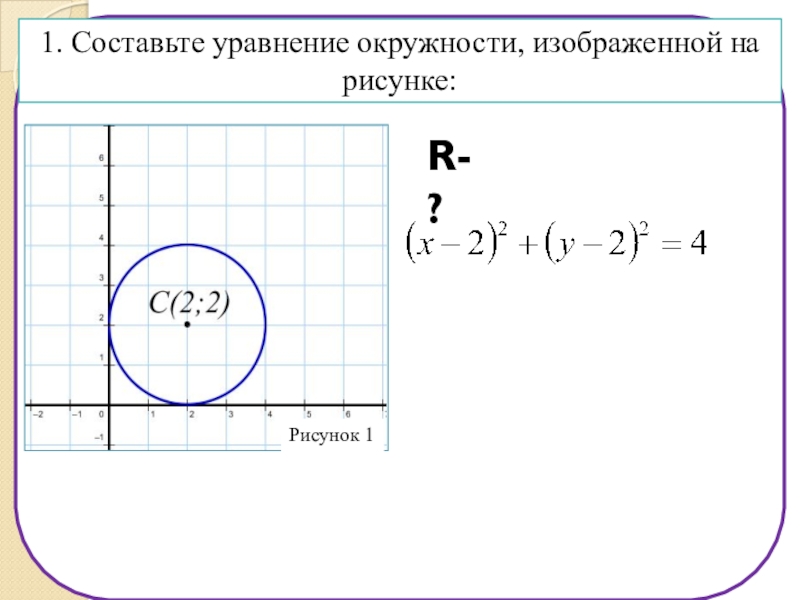
- 12. r4RRRR1. Составьте уравнение окружности, изображенной на рисунке:R-?
- 13. R rr0-2. Составьте уравнение окружности, изображенной на рисунке:R-?С (Хо;Уо)-?
- 14. 3. Заполните таблицу.
- 15. 4. Постройте в тетради окружности,
- 16. 5. Составьте уравнение окружности с центром А(3;2), проходящей через В(7;5).
- 17. Домашнее задание: п.91, №959(б, г, д), №967.
- 18. сегодня я узнал…было интересно…было трудно…я выполнял
Слайд 1Уравнение окружности
Урок геометрии в 9 классе
Учитель Жукова Ольга Петровна
МОУ Пречистенская СОШ
Слайд 2Цели урока:
Образовательные: Вывести уравнение окружности, рассмотрев решение этой задачи как одну
Уметь:
– Распознать уравнение окружности по предложенному уравнению, научить учащихся составлять уравнение окружности по готовому чертежу, строить окружность по заданному уравнению.
–Применять современные ИКТ для оформления результатов исследования.
Воспитательные: Формирование критического мышления.
Развивающие: Развитие умения составлять алгоритмические предписания и умение действовать в соответствии с предложенным алгоритмом.
Слайд 3Повторение
Запишите формулу нахождения координат середины отрезка.
Запишите формулу нахождения координат вектора.
Запишите формулу
Запишите формулу нахождения расстояния между точками (длины отрезка).
Слайд 4Повторение:
1. Даны точки А ( - 1; 7 ) и В
а) Найдите координаты середины отрезка АВ.
С ( 3; 4)
б) Найдите длину отрезка АВ.
|АВ| = 10
Слайд 5Повторение:
2. Найдите координаты вектора , если
3. Найдите расстояние между точками
А (а; 0) и В (b; 0).
Слайд 6 Уравнение окружности.
1. Дайте определение окружности.
2. Что такое центр и радиус
3. Как называется отрезок, соединяющий две точки окружности ?
4. Как называется хорда проходящая через центр окружности ?
Слайд 71 этап: Вывод формулы
Уравнение фигуры – это уравнение
с двумя переменными х
удовлетворяют координаты любой
точки фигуры.
Пусть дана окружность.
А(а;b) – центр окружности,
С(х ; у) – точка окружности,
М(х; у) – точка окружности.
Что можно сказать о взаимном расположении точек А и С на плоскости и точек А и М на плоскости?
Как можно сформулировать определение окружности?
Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки.
Слайд 8Вывод формулы
Пусть дана окружность.
А(а;b) – центр окружности,
С(х ; у) –
Найти расстояние между точками
А с С.
d 2 = АС 2 = (х – а)2 + (у – b)2,
Как можно назвать отрезок АС?
d = АС = R, следовательно
R 2 = (х – а)2 + (у – b)2
Слайд 9Формула I
(х – а)2 + (у – b)2 = R2
уравнение окружности,
А(а;b) − центр, R − радиус,
х и у – координаты точки окружности.
__________________________
А(2;4) – центр, R = 3, то
(х – 2)2 + (у – 4)2 = 32;
(х – 2)2 + (у – 4)2 = 9.
Слайд 10Формула II
(х – а)2 + (у – b)2 = R 2
Центр окружности О(0;0),
(х – 0)2 + (у – 0)2 = R 2,
х2 + у2 = R 2 − уравнение
окружности с центром в
начале координат. .
О (0;0) – центр, R = 5, тогда
х2 + у2 = 52;
х2 + у2 = 25.
Слайд 11Для того чтобы составить уравнение
окружности, нужно:
1) узнать координаты центра;
2) узнать длину
3) подставить координаты центра (а;b)
и длину радиуса R
в уравнение окружности
(х – а)2 + (у – b)2 = R2.
Слайд 15
4. Постройте в тетради окружности, заданные уравнениями:
1)(х – 5)2
2) (х + 1)2 + (у – 7)2 = 49.
Слайд 18 сегодня я узнал…
было интересно…
было трудно…
я выполнял задания…
я понял, что…
теперь я
я почувствовал, что…
я приобрел…
я научился…
у меня получилось …
я смог…
я попробую…
меня удивило…
урок дал мне для жизни…
мне захотелось…
Прием рефлексии «Незаконченное предложение»