ученики 7 класса
МБОУ Семлевской СОШ №1
Руководитель: Бардова И.А.
учитель математики
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Удивительный мир симметрии (7 класс)
Содержание
- 1. Презентация по геометрии на тему Удивительный мир симметрии (7 класс)
- 2. Слайд 2
- 3. «… быть прекрасным значит быть симметричным и
- 4. Математика и симметрия
- 5. Осевая симметрияДве точки, лежащие на одном перпендикуляре
- 6. Осевая симметрия Прямая L – ось симметрии.
- 7. Примеры симметричных фигур
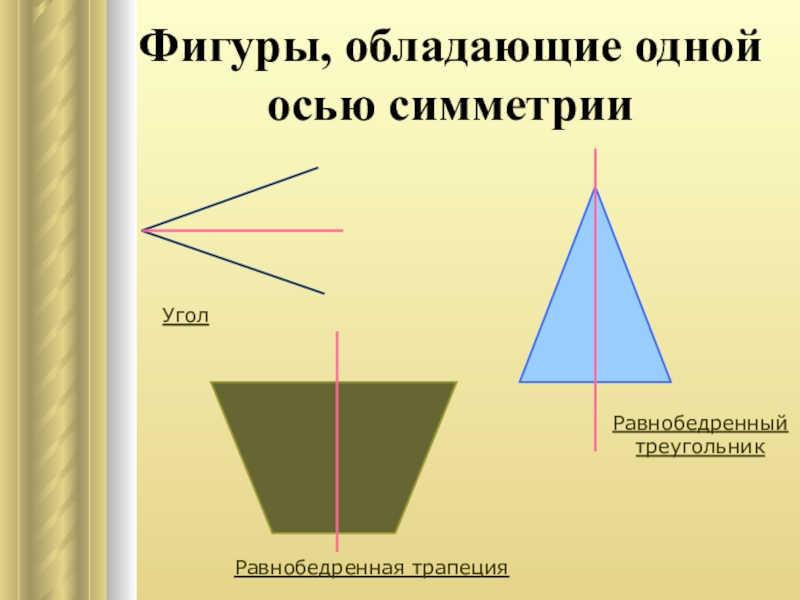
- 8. Фигуры, обладающие одной осью симметрииРавнобедренная трапецияРавнобедренный треугольникУгол
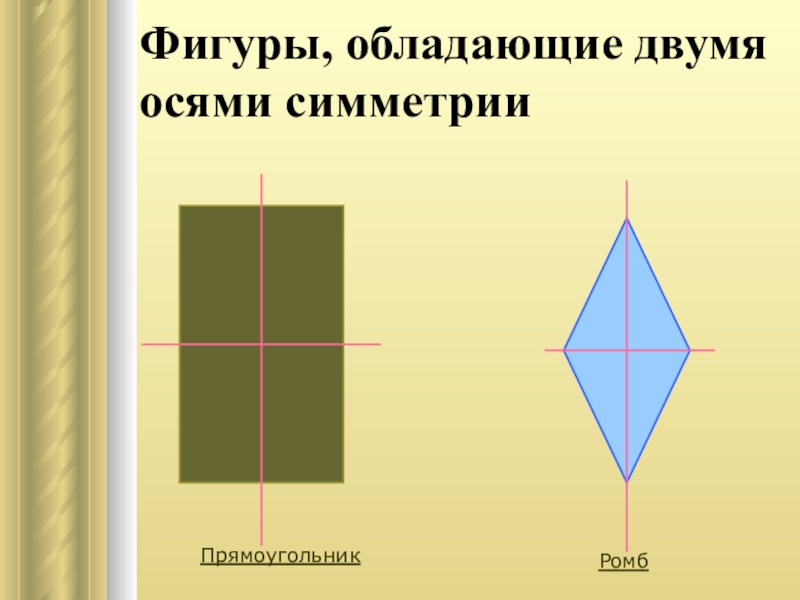
- 9. Фигуры, обладающие двумя осями симметрииПрямоугольникРомб
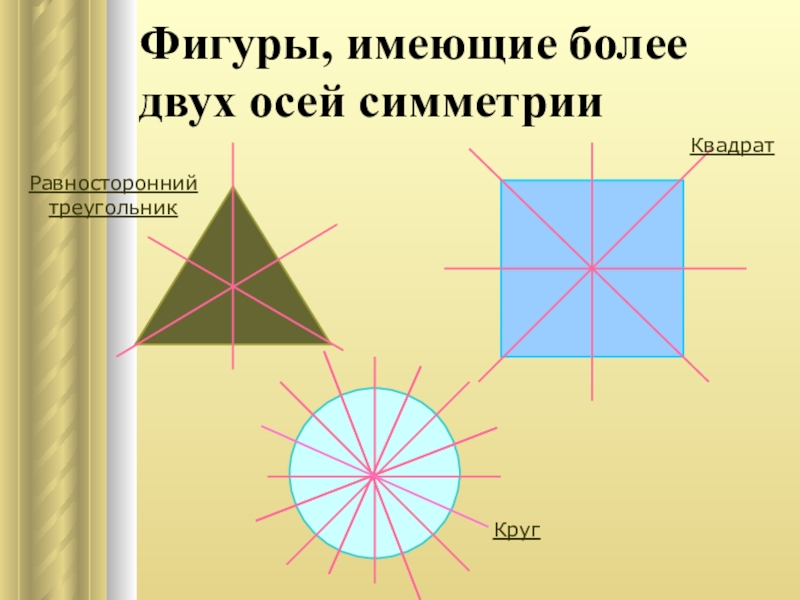
- 10. Фигуры, имеющие более двух осей симметрииРавносторонний треугольникКвадратКруг
- 11. Фигуры, не обладающие осевой симметриейПроизвольный треугольникПараллелограммНеправильный многоугольник
- 12. Центральная симметрияФигуры, симметричные относительно какой-либо точки называют
- 13. Симметрия относительно точкиАОТочки А и А1 называются
- 14. А1АОПостроить отрезок А1В1 симметричный отрезку АВ относительно
- 15. АВЗамечание. Если центр в вершине фигуры, то исходная и симметричная фигура имеют общую точку (точка С).С
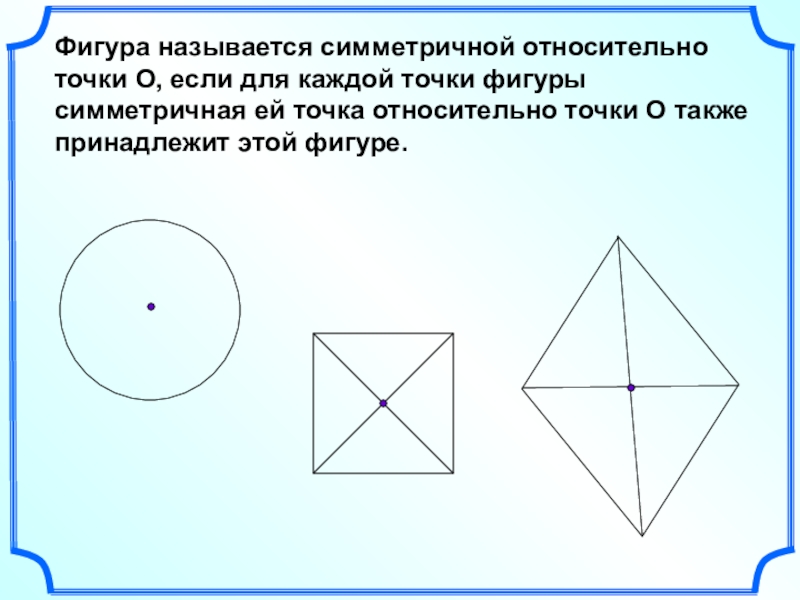
- 16. Фигура называется симметричной относительно точки О, если
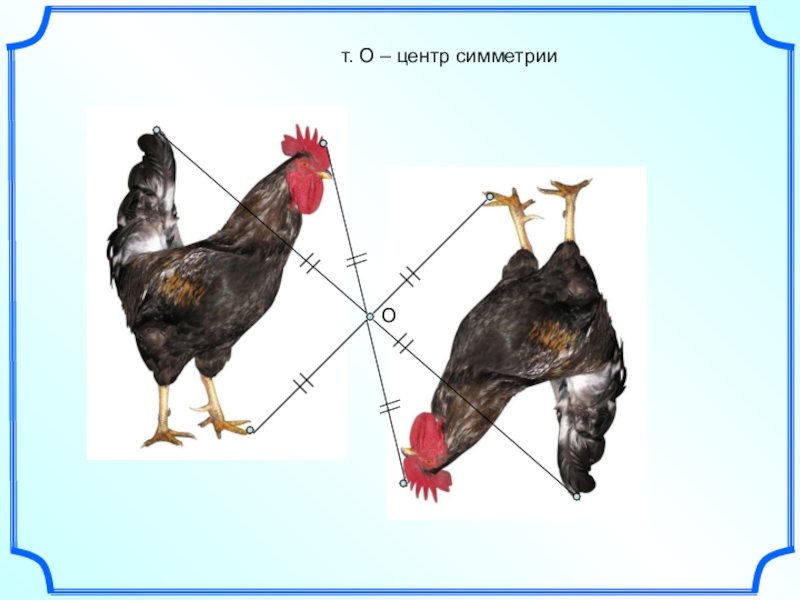
- 17. От. О – центр симметрии
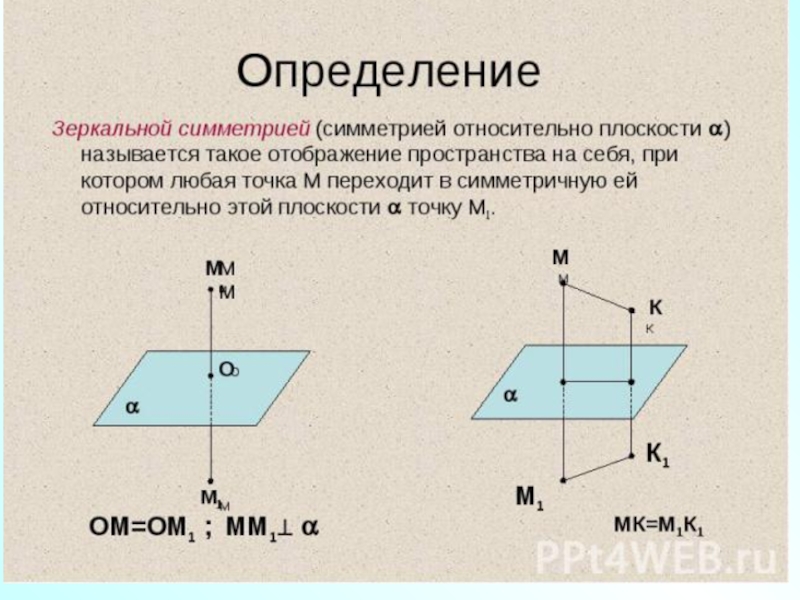
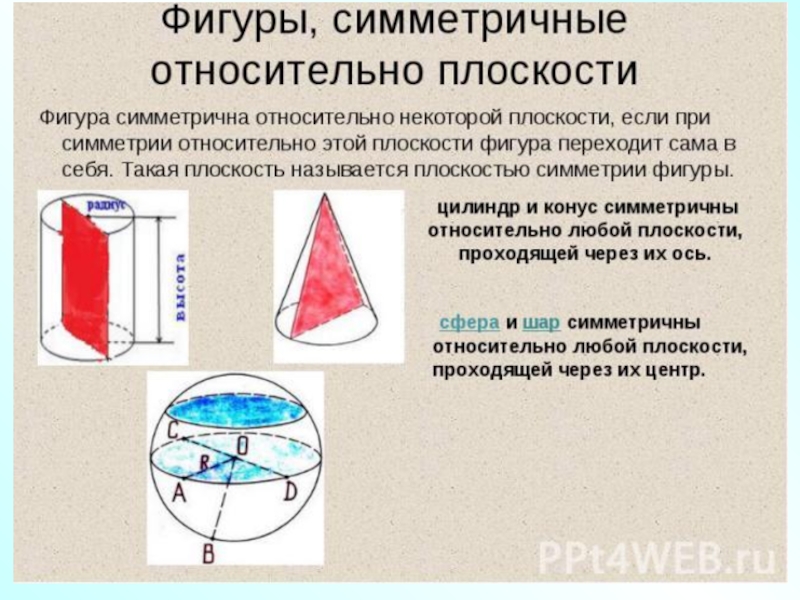
- 18. Зеркальная симметрия относительно плоскости
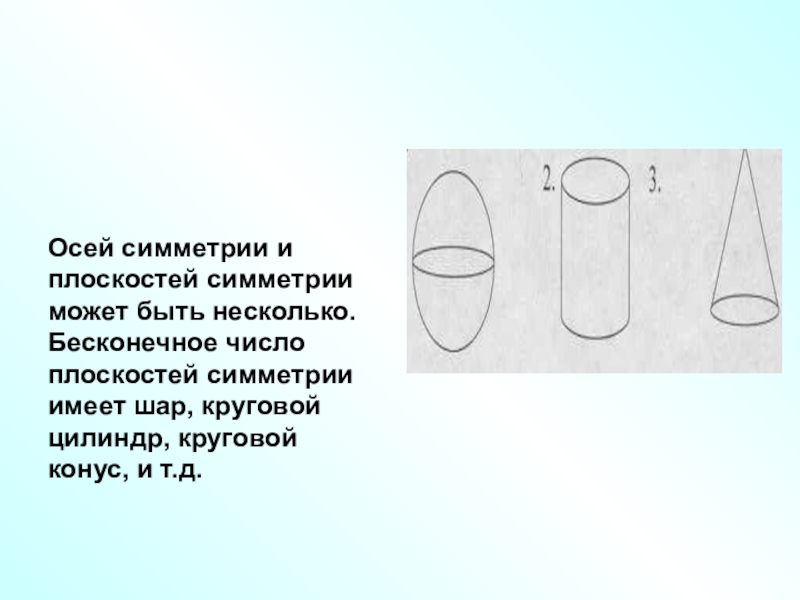
- 19. Осей симметрии и плоскостей симметрии может быть
- 20. Слайд 20
- 21. Слайд 21
- 22. Симметрия в природеВнимательное наблюдение показывает, что основу красоты многих форм, созданных природой, составляет симметрия.
«… быть прекрасным значит быть симметричным и соразмерным»
Слайд 3«… быть прекрасным
значит быть симметричным
и соразмерным»
Платон
Симметрия – это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство.
Г. Вейль
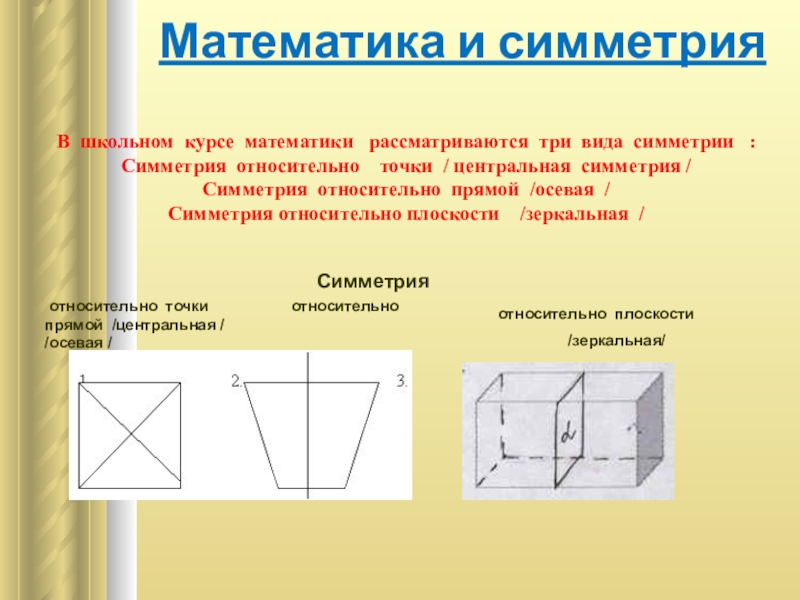
Слайд 4Математика и симметрия
Симметрия
относительно точки относительно прямой /центральная / /осевая /
относительно точки относительно прямой /центральная / /осевая /
относительно плоскости
/зеркальная/
В школьном курсе математики рассматриваются три вида симметрии :
Симметрия относительно точки / центральная симметрия /
Симметрия относительно прямой /осевая /
Симметрия относительно плоскости /зеркальная /
Слайд 5Осевая симметрия
Две точки, лежащие на одном перпендикуляре к данной прямой по
разные стороны и на одинаковом расстоянии от нее, называются симметричными относительно данной прямой.
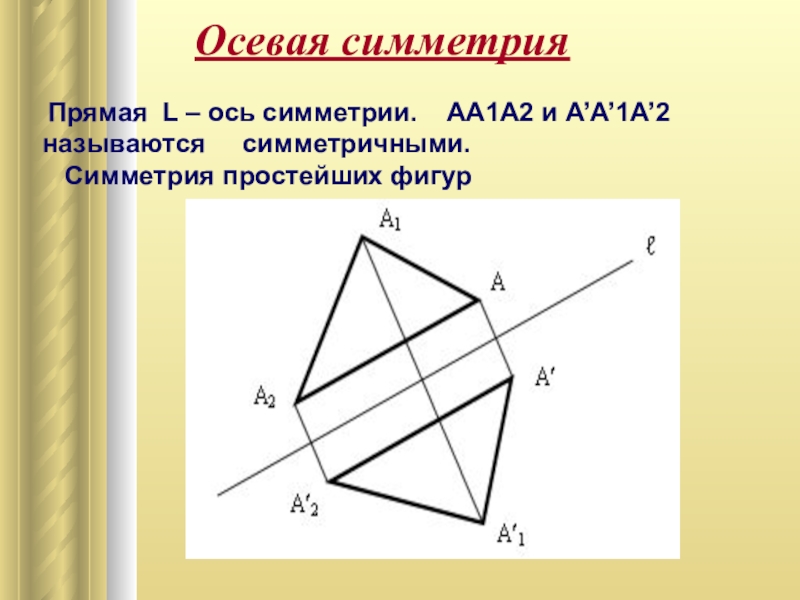
Слайд 6Осевая симметрия
Прямая L – ось симметрии. AA1A2 и А’A’1A’2
называются симметричными.
Симметрия простейших фигур
Симметрия простейших фигур
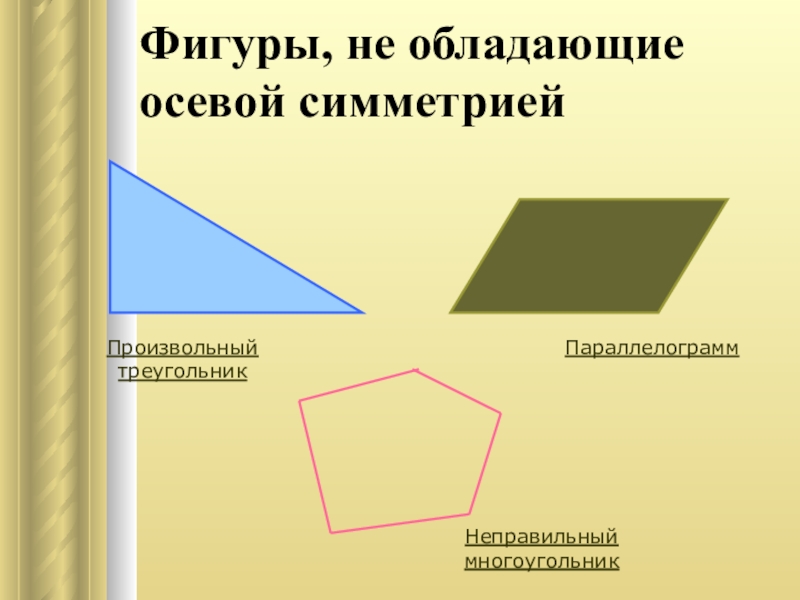
Слайд 11Фигуры, не обладающие осевой симметрией
Произвольный треугольник
Параллелограмм
Неправильный многоугольник
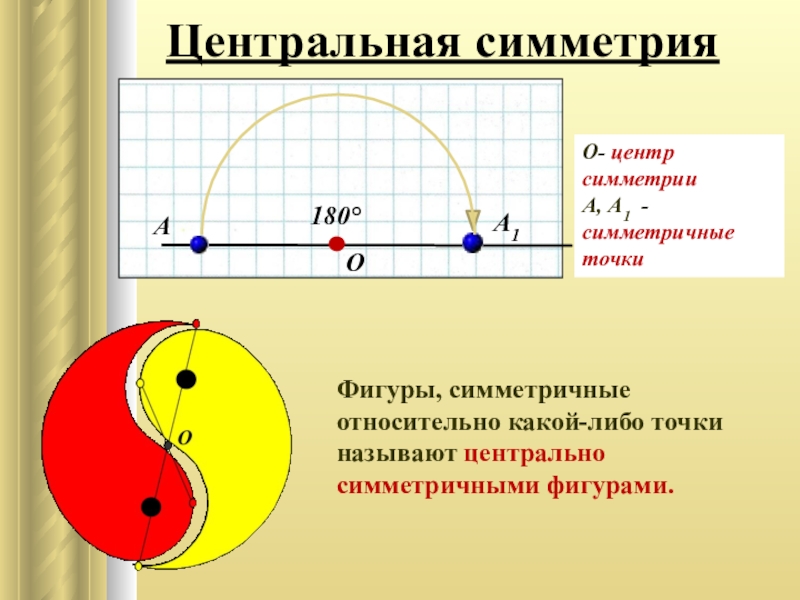
Слайд 12Центральная симметрия
Фигуры, симметричные относительно какой-либо точки называют центрально симметричными фигурами.
А
А1
О
180°
О- центр
симметрии
А, А1 - симметричные точки
А, А1 - симметричные точки
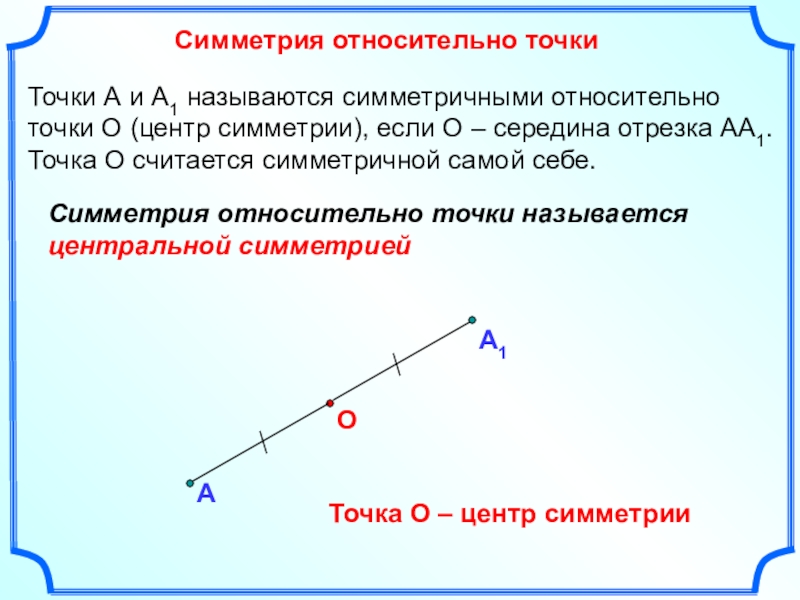
Слайд 13Симметрия относительно точки
А
О
Точки А и А1 называются симметричными относительно точки О
(центр симметрии), если О – середина отрезка АА1.
Точка О считается симметричной самой себе.
Точка О считается симметричной самой себе.
Точка О – центр симметрии
Симметрия относительно точки называется центральной симметрией
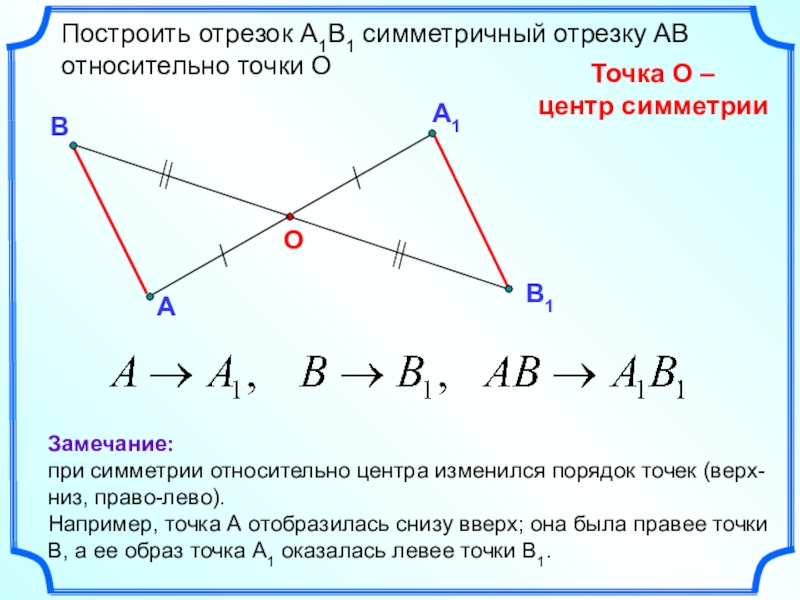
Слайд 14А1
А
О
Построить отрезок А1В1 симметричный отрезку АВ относительно точки О
Точка О –
центр симметрии
В
Замечание:
при симметрии относительно центра изменился порядок точек (верх-низ, право-лево).
Например, точка А отобразилась снизу вверх; она была правее точки В, а ее образ точка А1 оказалась левее точки В1.
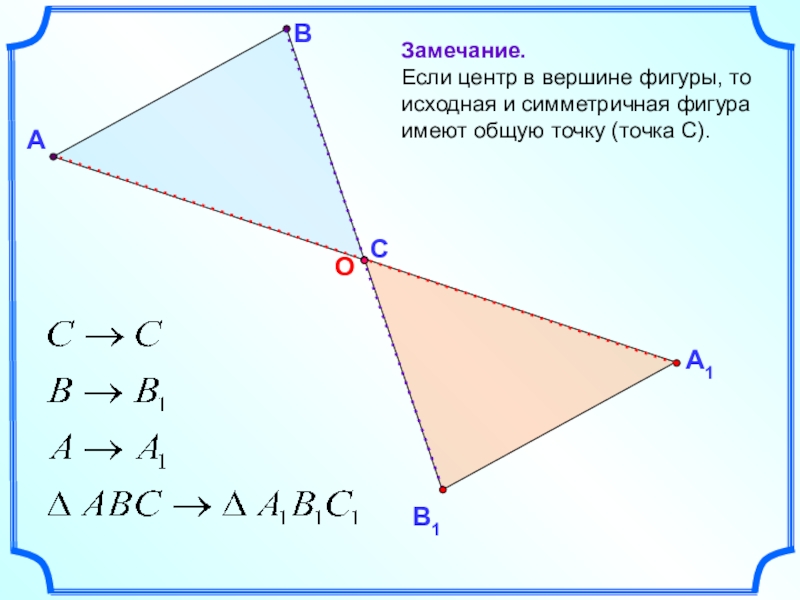
Слайд 15А
В
Замечание.
Если центр в вершине фигуры, то исходная и симметричная фигура
имеют общую точку (точка С).
С
Слайд 16Фигура называется симметричной относительно точки О, если для каждой точки фигуры
симметричная ей точка относительно точки О также принадлежит этой фигуре.
Слайд 19Осей симметрии и плоскостей симметрии может быть несколько. Бесконечное число плоскостей
симметрии имеет шар, круговой цилиндр, круговой конус, и т.д.
Слайд 22Симметрия в природе
Внимательное наблюдение показывает, что основу красоты многих форм, созданных
природой, составляет симметрия.
