- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Треугольники (7 класс)
Содержание
- 1. Презентация по геометрии на тему Треугольники (7 класс)
- 2. Определение:Треугольник - это геометрическая фигура, которая состоит
- 3. Равнобедренный треугольникРавнобедренный треугольник — это треугольник, в
- 4. Углы равнобедренного треугольникаЕсли треугольник является равнобедренным треугольником,
- 5. Медиана, биссектриса и высотаВ равнобедренном треугольнике медиана, биссектриса и высота,
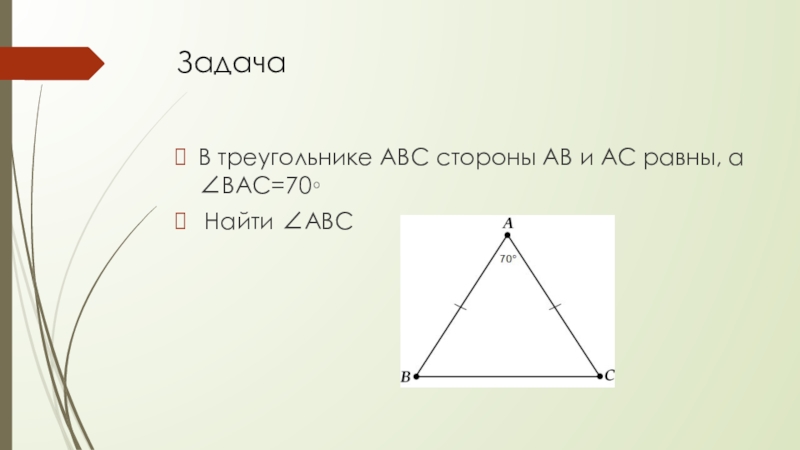
- 6. ЗадачаВ треугольнике ABC стороны AB и AC равны, а ∠BAC=70∘ Найти ∠ABC
- 7. Задача В треугольнике АВС боковые стороны АС
- 8. Решение:Внешний угол В равен 110°, значит, смежный
- 9. ЗадачаВ равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите
- 10. Решение:В равностороннем треугольнике ABC все углы равны
- 11. РАЗНОСТОРОННИЙ ТРЕУГОЛЬНИКРазносторонний треугольник - это треугольник, в
- 12. Равносторонний треугольникРавносторонний (правильный) треугольник - это треугольник,
- 13. Медиана биссектриса и высотаМедиана треугольника —
- 14. Медиана биссектриса и высота Биссектриса треугольника
- 15. Медиана биссектриса и высотаВысота треугольника —
- 16. Задача В треугольнике АВС точка D на
- 17. РешениеИз треугольника ADC видно, что он равнобедренный,
- 18. Задача: В треугольнике АВС проведена биссектриса АК.
- 19. Решение:Угол АКС является внешним для треугольника АВК
- 20. Прямоугольный треугольникПрямоугольным называется треугольник, у которого один из
- 21. Свойство прямоугольного треугольникаВ прямоугольном треугольнике, катет, лежащий против угла в 30°, равен половине гипотенузы
- 22. ЗадачаОдин острый угол прямоугольного треугольника на 60°
- 23. РешениеПусть один из острых углов треугольника равен
- 24. Спасибо за внимание
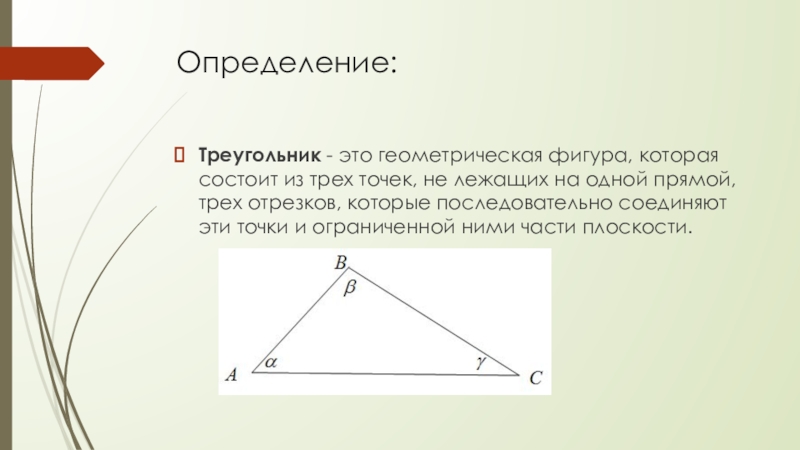
Определение:Треугольник - это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, трех отрезков, которые последовательно соединяют эти точки и ограниченной ними части плоскости.
Слайд 1Треугольники
Равнобедренные
Общего вида
Прямоугольные
Выполнила:
Педагог доп. образования
Столяренко Татьяна Валерьевна
Г. Владикавказ 2016 г.
Слайд 2Определение:
Треугольник - это геометрическая фигура, которая состоит из трех точек, не
лежащих на одной прямой, трех отрезков, которые последовательно соединяют эти точки и ограниченной ними части плоскости.
Слайд 3Равнобедренный треугольник
Равнобедренный треугольник — это треугольник, в котором две стороны равны
между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием.
Слайд 4Углы равнобедренного треугольника
Если треугольник является равнобедренным треугольником, то углы при его основании
равны
Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником.
Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником.
Слайд 5Медиана, биссектриса и высота
В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей
основанию, совпадают
Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным
Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным
Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным
Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным
Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным
Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным
Слайд 7Задача
В треугольнике АВС боковые стороны АС и АВ равны между
собой. Внешний угол при вершине В равен 110°. Найти угол С.
Слайд 8Решение:
Внешний угол В равен 110°, значит, смежный с ним внутренний угол
в треугольнике равен 180-10 = 70°.
Но внутренний угол В равен углу А, как углы при основании равнобедренного треугольника. Значит, угол А равен 70°.
А сумма внутренних углов треугольника равна 180°.
И если 2 из них равны по 70, то на долю третьего угла С приходится 180 — 70 — 70 = 40°.
Ответ: угол с равен 40°.
Но внутренний угол В равен углу А, как углы при основании равнобедренного треугольника. Значит, угол А равен 70°.
А сумма внутренних углов треугольника равна 180°.
И если 2 из них равны по 70, то на долю третьего угла С приходится 180 — 70 — 70 = 40°.
Ответ: угол с равен 40°.
Слайд 9Задача
В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите
Слайд 10Решение:
В равностороннем треугольнике ABC все углы равны 60°.
Биссектрисы CN и
AM делят углы пополам,
поэтому LACN= LMAC = 60° : 2 = 30°
Сумма углов в треугольнике равна 180°,
поэтому LAPC = 180° - 30° - 30° = 120°
Вертикальные углы равны, следовательно, LMPN = LAPC =120°
Ответ: 120°.
поэтому LACN= LMAC = 60° : 2 = 30°
Сумма углов в треугольнике равна 180°,
поэтому LAPC = 180° - 30° - 30° = 120°
Вертикальные углы равны, следовательно, LMPN = LAPC =120°
Ответ: 120°.
Слайд 11РАЗНОСТОРОННИЙ ТРЕУГОЛЬНИК
Разносторонний треугольник - это треугольник, в котором все углы, а
значит и все стороны попарно различны.
(Разносторонний треугольник может быть остроугольным, прямоугольным и тупоугольным).
(Разносторонний треугольник может быть остроугольным, прямоугольным и тупоугольным).
Слайд 12Равносторонний треугольник
Равносторонний (правильный) треугольник - это треугольник, у которого все стороны
и все углы равны (каждый угол равен 60°).
Слайд 13Медиана биссектриса и высота
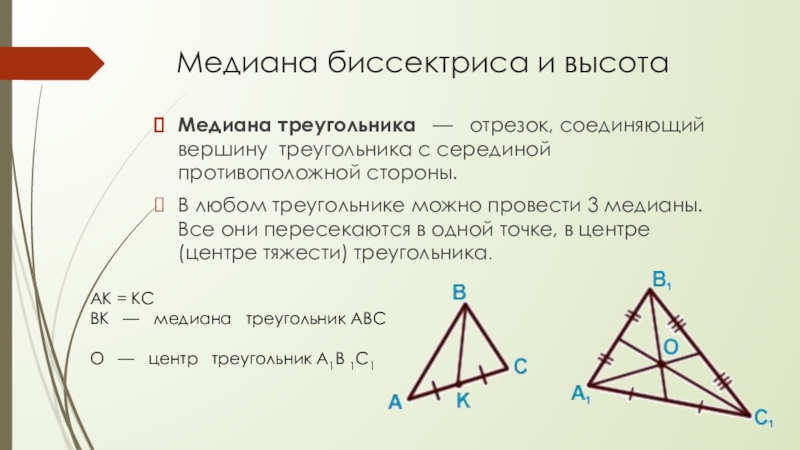
Медиана треугольника — отрезок, соединяющий вершину
треугольника с серединой противоположной стороны.
В любом треугольнике можно провести 3 медианы. Все они пересекаются в одной точке, в центре (центре тяжести) треугольника.
В любом треугольнике можно провести 3 медианы. Все они пересекаются в одной точке, в центре (центре тяжести) треугольника.
AK = KC
BK — медиана треугольник ABC
О — центр треугольник A1B 1C1
Слайд 14Медиана биссектриса и высота
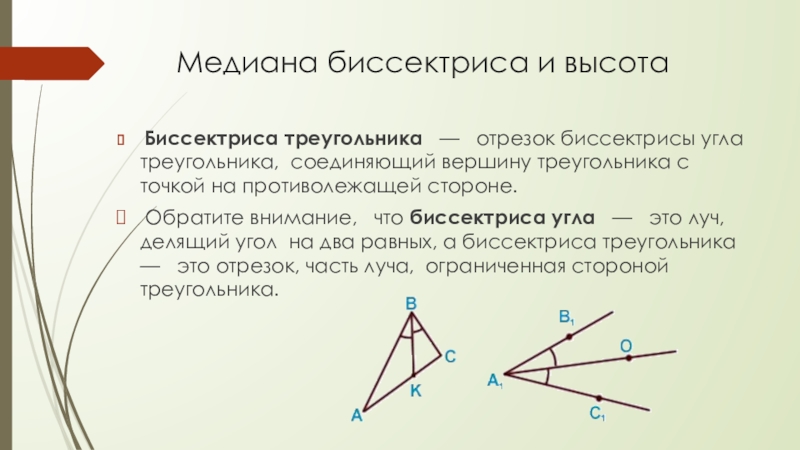
Биссектриса треугольника — отрезок биссектрисы
угла треугольника, соединяющий вершину треугольника с точкой на противолежащей стороне.
Обратите внимание, что биссектриса угла — это луч, делящий угол на два равных, а биссектриса треугольника — это отрезок, часть луча, ограниченная стороной треугольника.
Обратите внимание, что биссектриса угла — это луч, делящий угол на два равных, а биссектриса треугольника — это отрезок, часть луча, ограниченная стороной треугольника.
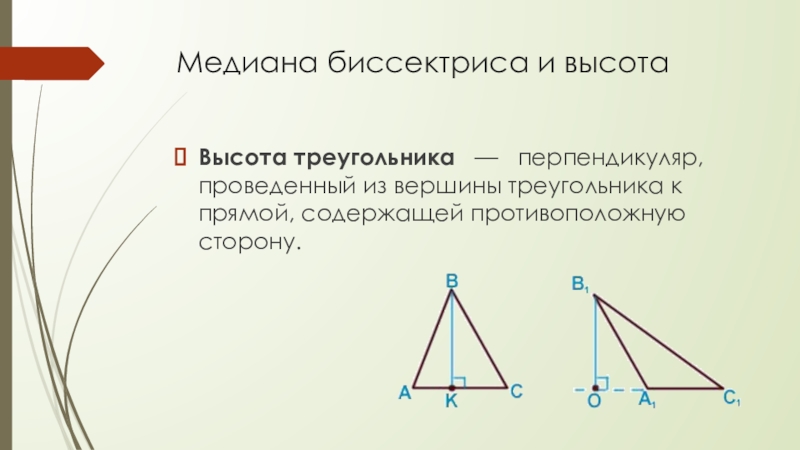
Слайд 15Медиана биссектриса и высота
Высота треугольника — перпендикуляр, проведенный из
вершины треугольника к прямой, содержащей противоположную сторону.
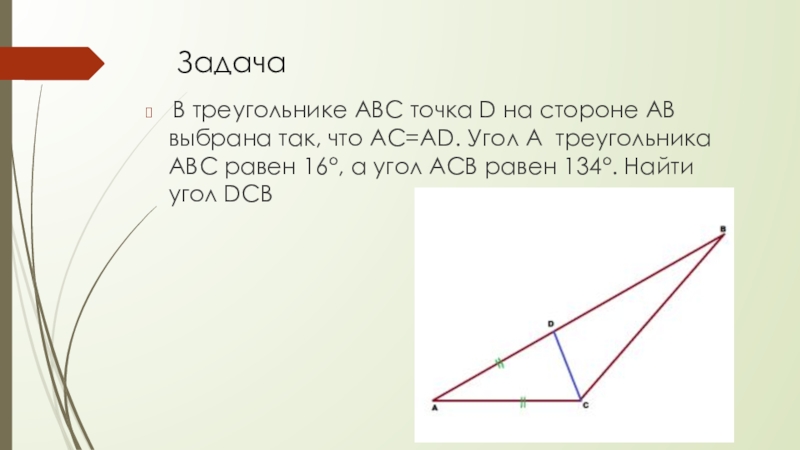
Слайд 16Задача
В треугольнике АВС точка D на стороне АВ выбрана так,
что АС=AD. Угол А треугольника АВС равен 16°, а угол АСВ равен 134°. Найти угол DCB
Слайд 17Решение
Из треугольника ADC видно, что он равнобедренный, поскольку 2 боковые стороны
его равны.
А в равнобедренном треугольнике углы при основании равны.
Значит, угол ADC равен углу АСВ.
Но сумма внутренних углов треугольника равна 180°.
Отсюда, сумма двух углов при основании равна 180-16=164°.
Углы, как мы уже сказали, равны. Поэтому, каждый из них равен 164:2 = 82°.
Угол АСВ по условию равен 134°.
А если внутри угла провести луч, то он разделит угол на 2 угла, сумма градусных мер которых будет равна градусной мере первоначального угла.
Т.е. Угол АСВ равен сумме углов АCD и DCB.
Отсюда, угол DCB равен 134 — 82 = 52°.
Ответ: угол DCB равен 52°.
А в равнобедренном треугольнике углы при основании равны.
Значит, угол ADC равен углу АСВ.
Но сумма внутренних углов треугольника равна 180°.
Отсюда, сумма двух углов при основании равна 180-16=164°.
Углы, как мы уже сказали, равны. Поэтому, каждый из них равен 164:2 = 82°.
Угол АСВ по условию равен 134°.
А если внутри угла провести луч, то он разделит угол на 2 угла, сумма градусных мер которых будет равна градусной мере первоначального угла.
Т.е. Угол АСВ равен сумме углов АCD и DCB.
Отсюда, угол DCB равен 134 — 82 = 52°.
Ответ: угол DCB равен 52°.
Слайд 18Задача:
В треугольнике АВС проведена биссектриса АК. Угол АКС равен 94°,
а угол АВС равен 62°. Найти угол С треугольника АВС.
Слайд 19Решение:
Угол АКС является внешним для треугольника АВК и равным сумме двух
внутренних углов, не смежных с ним, т.е. сумме углов В и ВАК.
Отсюда мы можем найти угол ВАК.
Он равен 94 — 62 = 32°.
Поскольку АК — биссектриса угла А, то угол КАС тоже равен 32°.
А теперь, рассматривая треугольник АКС и зная в нём 2 угла, можно найти третий.
∠С = 180 — 32 — 94 = 54°.
Ответ: угол С равен 54
Отсюда мы можем найти угол ВАК.
Он равен 94 — 62 = 32°.
Поскольку АК — биссектриса угла А, то угол КАС тоже равен 32°.
А теперь, рассматривая треугольник АКС и зная в нём 2 угла, можно найти третий.
∠С = 180 — 32 — 94 = 54°.
Ответ: угол С равен 54
Слайд 20Прямоугольный треугольник
Прямоугольным называется треугольник, у которого один из углов прямой (на рисунке
это угол С)
Стороны, которые образуют прямой угол ( АС и ВС ), называются катетами, а сторона, лежащая против прямого угла - гипотенузой (АВ ).
Стороны, которые образуют прямой угол ( АС и ВС ), называются катетами, а сторона, лежащая против прямого угла - гипотенузой (АВ ).
Слайд 21Свойство прямоугольного треугольника
В прямоугольном треугольнике, катет, лежащий против угла в 30°,
равен половине гипотенузы
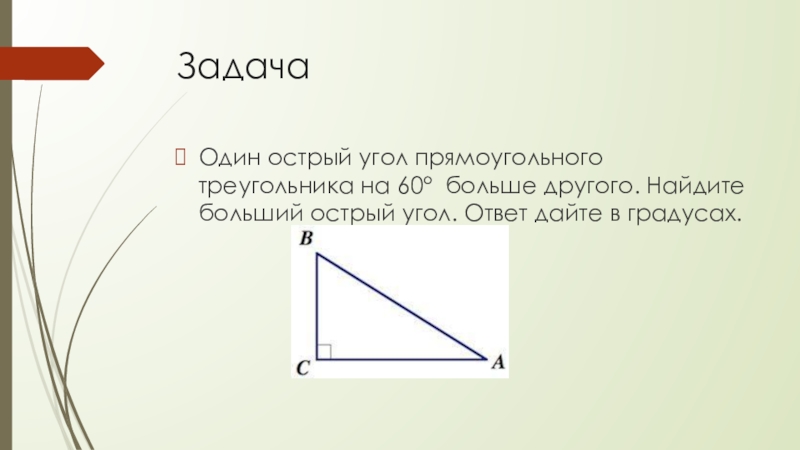
Слайд 22Задача
Один острый угол прямоугольного треугольника на 60° больше другого. Найдите больший
острый угол. Ответ дайте в градусах.
Слайд 23Решение
Пусть один из острых углов треугольника равен x градусов, тогда согласно
условию задачи второй острый угол равен 60+x градусов.
Поскольку на острые углы прямоугольного треугольника приходится 90°, то x+60+x=90;
2x=30;
x=15;
Тогда больший угол равен 15°+60°=75°.
Ответ: 75°.
Поскольку на острые углы прямоугольного треугольника приходится 90°, то x+60+x=90;
2x=30;
x=15;
Тогда больший угол равен 15°+60°=75°.
Ответ: 75°.