- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Теорема Пифагора (8 класс)
Содержание
- 1. Презентация по геометрии на тему Теорема Пифагора (8 класс)
- 2. Слайд 2
- 3. Слайд 3
- 4. Слайд 4
- 5. Теорема: в прямоугольном треугольнике квадрат гипотенузы равен
- 6. Площадь квадрата
- 7. Доказательство Бхаскары
- 8. Слайд 8
- 9. Если a2 +b2= с2, то
- 10. Теорема: если квадрат одной стороны равен сумме
- 11. Для крепления мачты нужно установить 4 троса.
- 12. Пифагоровы треугольники- длины сторон выражаются целыми числами.Некоторые
- 13. № 483, 484 (а,б), 485, 486№ 483Найдите
- 14. Домашнее задание № 484(в,г), 487
Слайд 1Теорема Пифагора подготовила: Львова Оксана Александровна, учитель математики МАОУ «СОШ №40»
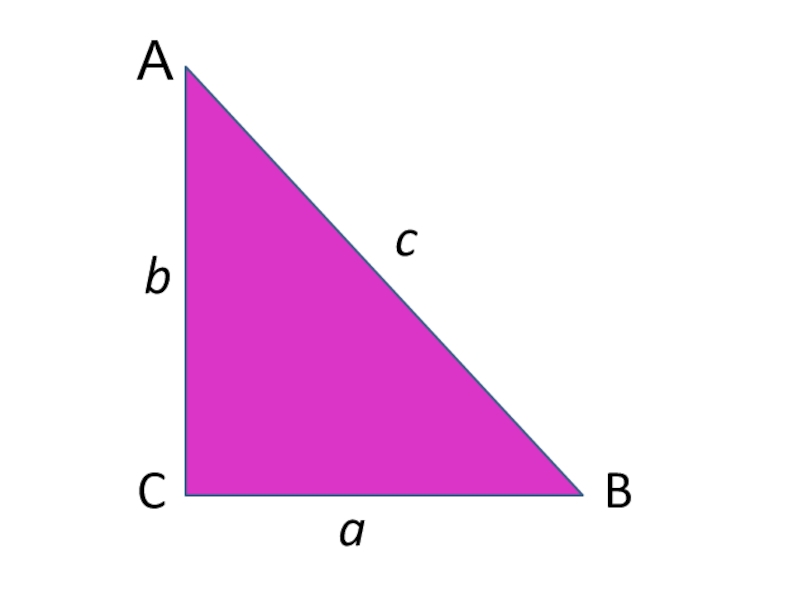
Слайд 5Теорема: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов.
с2=a2+b2.
Доказательство:
Рассмотрим прямоугольный треугольник с катетами a,b и гипотенузой с.
Докажем с2=a2+b2.
Достроим треугольник АВС до квадрата со стороной a+b.
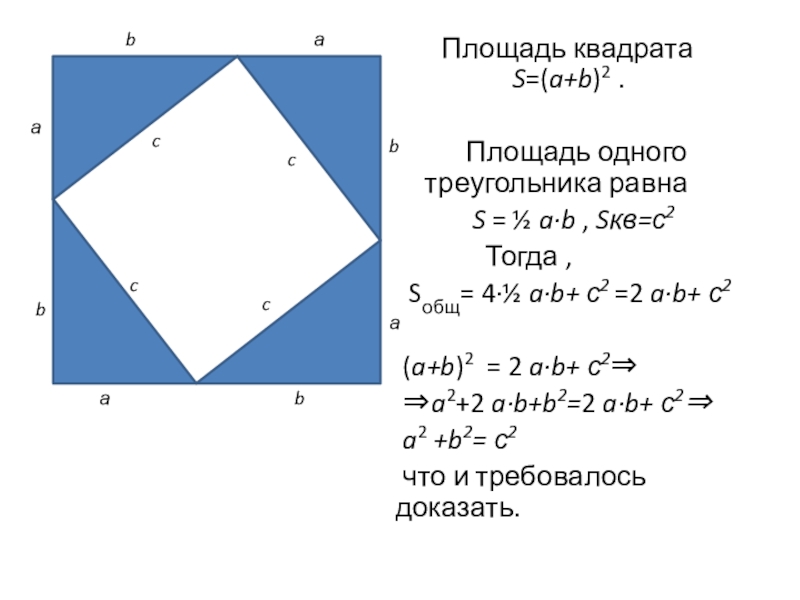
Слайд 6Площадь квадрата
Площадь одного треугольника равна
S = ½ a·b , Sкв=с2
Тогда ,
Sобщ= 4·½ a·b+ с2 =2 a·b+ с2
(a+b)2 = 2 a·b+ с2
a2+2 a·b+b2=2 a·b+ с2
a2 +b2= с2
что и требовалось доказать.
а
а
а
а
b
b
b
b
c
c
c
c
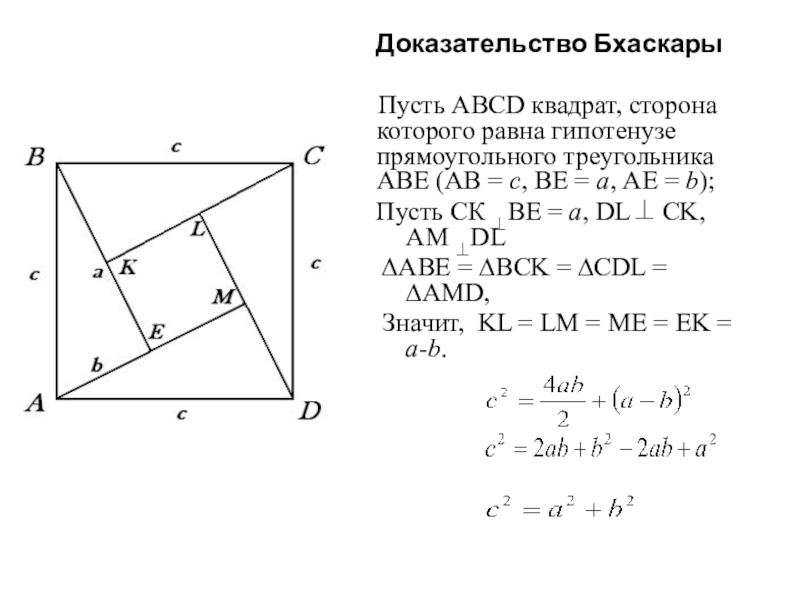
Слайд 7Доказательство Бхаскары
Пусть АВСD квадрат, сторона которого равна гипотенузе прямоугольного треугольника АВЕ (АВ = с, ВЕ = а, АЕ = b);
Пусть СК ВЕ = а, DL CK, AM DL
ΔABE = ∆BCK = ∆CDL = ∆AMD,
Значит, KL = LM = ME = EK = a-b.
Слайд 9Если a2 +b2= с2, то
Если известен катет и гипотенуза, можно найти другой катет. Пусть неизвестен катет а, то
a2 = с2 - b2 , то (**)
Теорема Пифагора для равнобедренного треугольника:
а
а
с
Слайд 10Теорема: если квадрат одной стороны равен сумме квадратов двух других сторон,
Доказательство:
Пусть в треугольнике АВС АС2 +ВС2= АВ2. Докажем, что угол С – прямой.
Возьмем ∆А1В1С 1 с прямым углом С1 , у которого АС=А1С1, ВС=В1С1. то по теореме Пифагора А1В12 = АС2 +ВС2, но по условию АС2 +ВС2= АВ2, то А1В12= АВ2 и А1В1= АВ. Значит, С=С1-прямой.
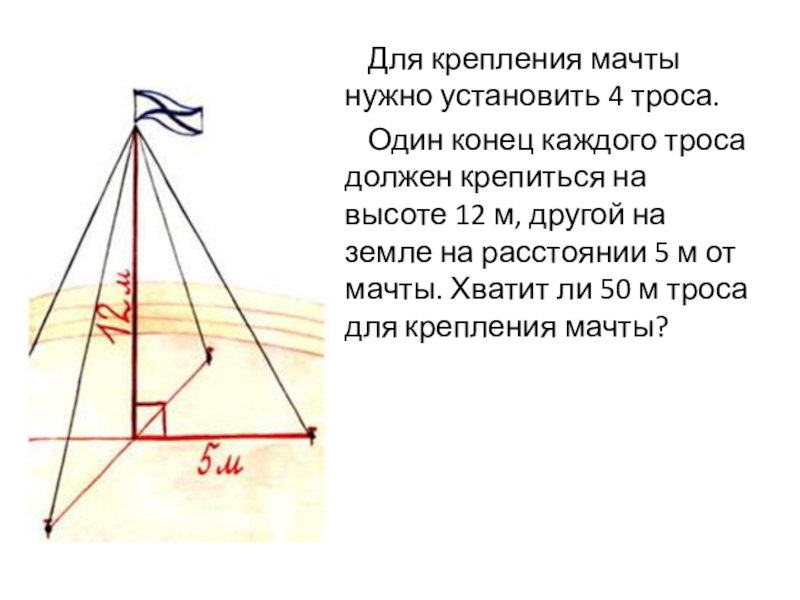
Слайд 11Для крепления мачты нужно установить 4 троса.
Один конец каждого троса
Слайд 12Пифагоровы треугольники- длины сторон выражаются целыми числами.
Некоторые пифагоровы тройки:
(3, 4, 5),
Слайд 13№ 483, 484 (а,б), 485, 486
№ 483
Найдите гипотенузу прямоугольного треугольника по
а) а=6, b=8; b) а=5, b=6; c) a=3/7, b=4/7; d) а=8, b=8 3.
№484
В треугольнике а и b – катеты, с – гипотенуза, найдите b
а=12, c=13, b) а=7, c=9.
№485
В прямоугольном треугольнике один угол равен 300, гипотенуза равна 10, чему равны а и b.
№486
В прямоугольнике АВСВ сторона АВ=5 и диагональ АС=13. Найти AD.