- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Теорема Пифагора 8 класс
Содержание
- 1. Презентация по геометрии на тему Теорема Пифагора 8 класс
- 2. Слайд 2
- 3. Домашняя работа № 472 Площадь прямоугольного треугольника
- 4. Пифагор Самосскийо. Самос
- 5. Пифагорейцами было сделано много важных открытий в арифметике и геометрии.Пифагор Самосский
- 6. «Ослиный мост»Доказательство теоремы Пифагора считалось в кругах
- 7. Что изображено? Вопросы Чему равна сумма острых
- 8. Дано: ∆ ABC,
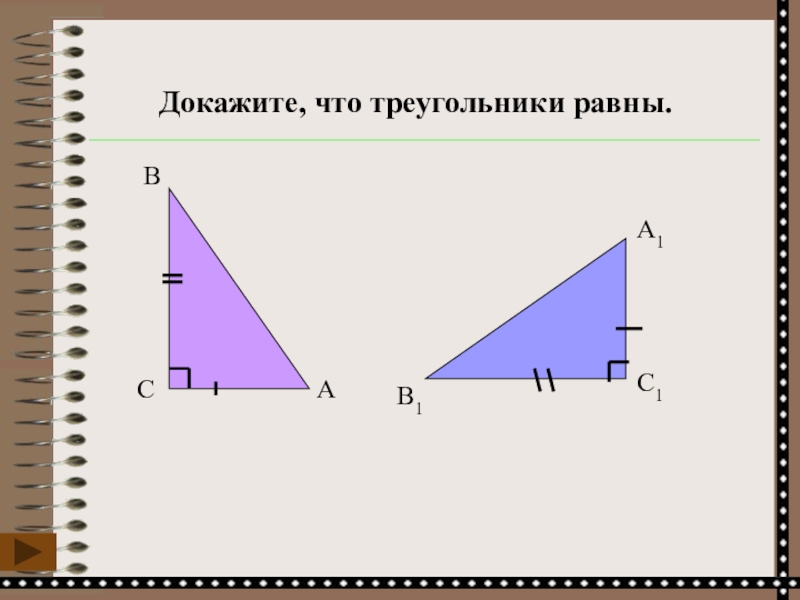
- 9. Докажите, что треугольники равны.
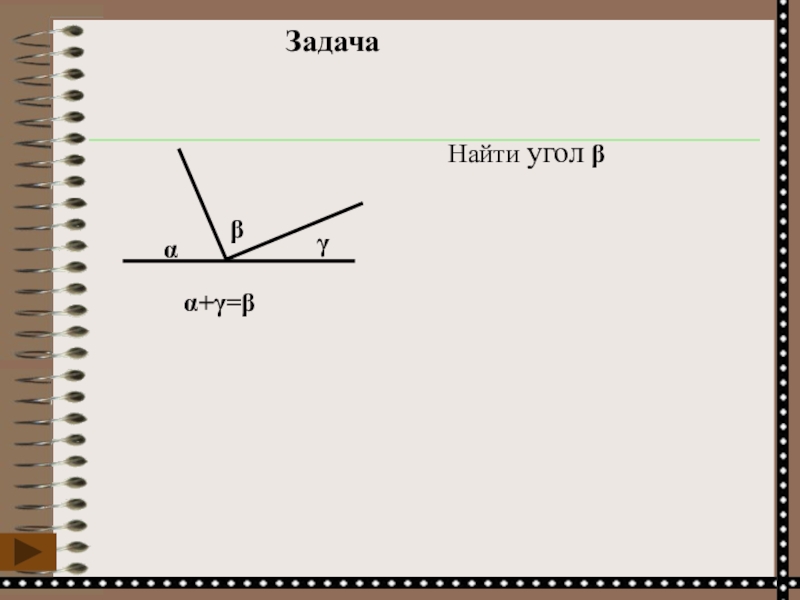
- 10. Найти угол β Задача
- 11. Доказать: KMNP - квадрат Что изображено?Из чего
- 12. ДоказательствоABCD - квадрат, AB = a +
- 13. Теорема Пифагора Итак,Если дан нам треугольник,И притом
- 14. История теоремы ПифагораПифагор Самосскийок. 580 – ок. 500 до н.э.
- 15. Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли
- 16. Физминутка Встали дружно, потянулисьАполлону улыбнулись!Богу Зевсу наш
- 17. № 483Дано: ∆АВС, ∠С=90º, а=6, b=8Найти: с.Решение:∆АВС
- 18. с² = а2 + b2№ 48423b2b121351213² =
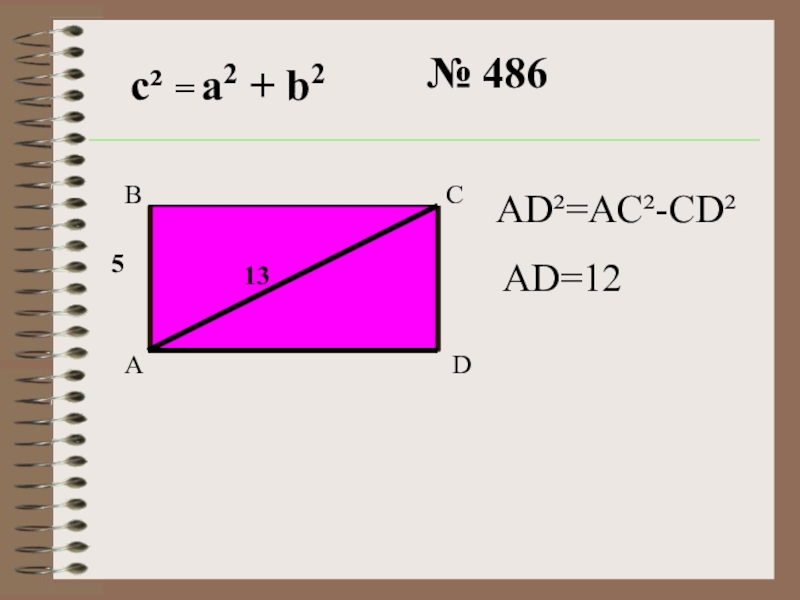
- 19. с² = а2 + b2№ 486513ABDCAD²=AC²-CD²AD=12
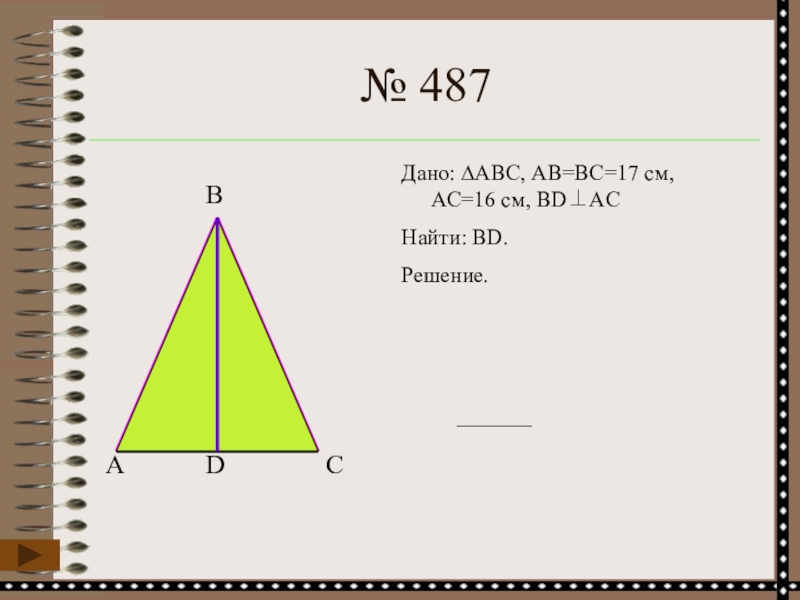
- 20. № 487Дано: ∆АВС, АВ=ВС=17 см, АС=16 см, BD⊥ACНайти: BD.Решение.АСBD
- 21. Слайд 21
- 22. Пифагор - мыслительЗадание: собрать из
- 23. Домашнее задание:п. 54№ 483 (в); № 484 (б, г); 486(б, в)
- 24. Спасибо за урок
Слайд 3Домашняя работа
№ 472
Площадь прямоугольного треугольника
равна 168 см². Найдите его
Дано: ∆ABC, BС=7,5 см, АC=3,2 см, АM⊥BC, BN⊥AC, AM=2,4 cм Найти: BN
Решение: S∆ABC=½АМ·СВ=½·2,4·7,5=9 см²
S∆ABC=½BN·AС ⇒ BN=2·S∆ABC:АС=2·9:3,2=5,625 см
Ответ: 5,625 см.
Дано: ∆ABC, ∠С=90º, АC:ВС=7:12, S∆ABC=168 см² Найти: АС, BС.
№ 470
Две стороны треугольника равны
7,5 см и 3,2 см. Высота, проведенная
к большей стороне, равна 2,4 см.
Найдите высоту, проведенную к
меньшей из данных сторон.
Решение: S∆ABC=½АС·ВС
168=½7х·12х
168=42х²
х=2
АС=14 см, ВС=24 см
Ответ: 14 см и 24 см.
Слайд 6«Ослиный мост»
Доказательство теоремы Пифагора считалось в кругах учащихся средних веков очень
Слабые ученики, заучивавшие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть
теорему Пифагора, служившую для них вроде непреодолимого моста.
Слайд 7Что изображено?
Вопросы
Чему равна сумма острых углов в прямоугольном треугольнике?
∠А
Чему равна площадь этого треугольника?
Как называются стороны АС и ВС?
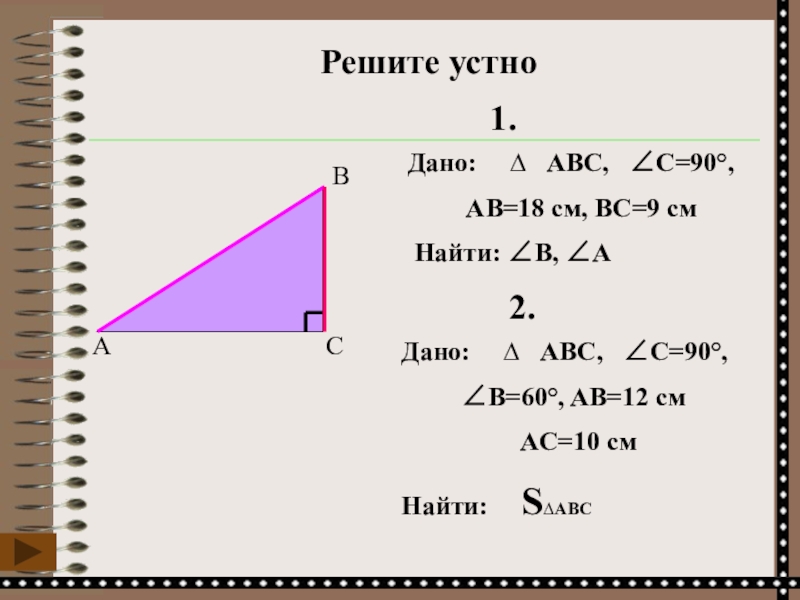
Слайд 8Дано: ∆ ABC, ∠C=90°,
∠B=60°, AB=12
AC=10 см
Найти: S∆АВС
Решите устно
C
A
B
Дано: ∆ ABC, ∠C=90°,
AB=18 см, ВC=9 см
Найти: ∠B, ∠А
1.
2.
Слайд 11Доказать: KMNP - квадрат
Что изображено?
Из чего он состоит?
Докажите, что треугольник
KВМ
Что можно сказать о площадях этих треугольников?
Доказательство
В четырехугольнике KMNP
все стороны равны с.
Найдем величину угла KMN.
∠1 + ∠2 = 90° и ∠1 = ∠3⇒
⇒∠2 + ∠3 =90°⇒∠KМN=90°.
Аналогично можно доказать, что все углы в четырехугольнике KMNP прямые, а это и означает, что KMNP - квадрат.
Решите устно
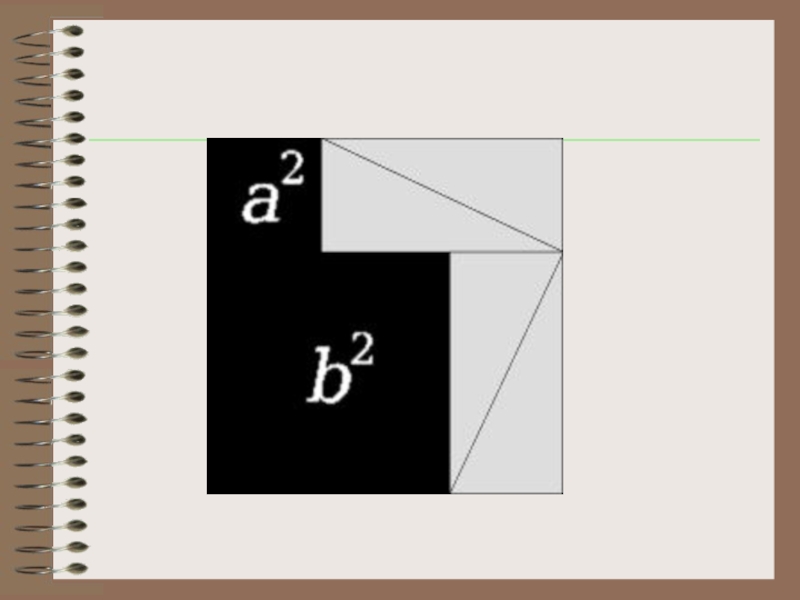
Слайд 12Доказательство
ABCD - квадрат, AB = a + b,
S ABCD =
2. Квадрат ABCD состоит из четырех равных прямоугольных треугольников, одним из которых является треугольник APK, и квадрата KMNP со стороной с, значит
SABCD = 4SAPK + SKMNP
a2+ 2ab +b2 = 2ab + c2
a2 + b2 = c2
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема Пифагора
Слайд 13Теорема Пифагора
Итак,
Если дан нам треугольник,
И притом с прямым углом,
То квадрат
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим -
И таким простым путем
К результату мы придем.
Слайд 15Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли ее так же “ветряной
Слайд 16Физминутка
Встали дружно, потянулись
Аполлону улыбнулись!
Богу Зевсу наш поклон
Многократным будет он.
Руки вверх
Всем вам верность мы храним.
Тело наше сделай круг
Повторив Деметры путь
Готовы из знаний
плести сотни сот
Поможет нам в этом
весь пантеон.
Слайд 17№ 483
Дано: ∆АВС, ∠С=90º,
а=6, b=8
Найти: с.
Решение:
∆АВС – прямоугольный с гипотенузой АВ.
с²=а²+b²
с²=6²+8²
с²=36+64
с²=100
c=10
Ответ: 10
с² = а2 + b2
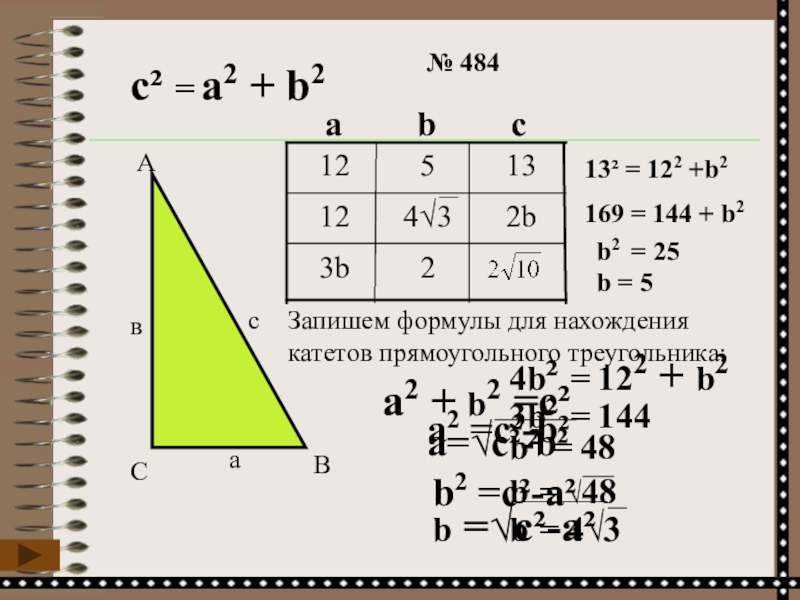
Слайд 18с² = а2 + b2
№ 484
2
3b
2b
12
13
5
12
13² = 122 +b2
169 = 144
b2 = 25
b = 5
4b² = 122 + b2
3b² = 144
b² = 48
а2 + b2 =c²
а2 =c²-b²
b2 =c²-a²
Запишем формулы для нахождения катетов прямоугольного треугольника: