- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Теорема Пифагора ( 8 класс)
Содержание
- 1. Презентация по геометрии на тему Теорема Пифагора ( 8 класс)
- 2. Одна из основополагающих теорем евклидовой геометрии, устанавливающая
- 3. СодержаниеТеорема ПифагораФормулировкиИстория теоремыДоказательства теоремыПрименениеЗаключение
- 4. .У Евклида эта теорема гласит: "В прямоугольном
- 5. История
- 6. Слайд 6
- 7. Способ построения
- 8. История
- 9. История
- 10. Пифагор Самосский (ок. 580 – ок. 500 г.до.н.э.)
- 11. Биография ПифагораВеликий ученый Пифагор родился
- 12. Жизнь Пифагора
- 13. Слайд 13
- 14. Открытия Пифагорейцев Теорема о сумме
- 15. ...Прошло 20 лет. Слава о братстве
- 16. Если дан нам треугольникИ притом с прямым
- 17. Теорема ПифагораВ прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетовa2+b2 =c2
- 18. Доказательство с - гипотенуза a,b - катеты abcДостроим треугольник до квадрата со стороной a+b
- 19. Слайд 19
- 20. Обратная теорема Если квадрат
- 21. Доказательство Пусть в треугольнике АВС АВ2=АС2+ВС2.Докажем,
- 22. Слайд 22
- 23. Эти доказательства основаны на разложении квадратов, построенных
- 24. Аддитивные
- 25. Аддитивные
- 26. Доказательства методом построения
- 27. Доказательства методом построения
- 28. Доказательства методом построения
- 29. Доказательства методом построения
- 30. Слайд 30
- 31. Алгебраический метод доказательства
- 32. Доказательства методом дополнения
- 33. Доказательство методом вычитания
- 34. Слайд 34
- 35. Завершая обзор примеров различных доказательств, приведем еще
- 36. Как уже было сказано выше, древние
- 37. Докажем, что этот треугольник
- 38. Слайд 38
- 39. Слайд 39
- 40. Упрощенное доказательство Евклида
- 41. Доказательство основанное на
- 42. Доказательство индийского математика
- 43. Векторное
- 44. Применение теоремы
- 45. Применение теоремы
- 46. Применение теоремы
- 47. Применение теоремы
- 48. Применение теоремы
- 49. Заключение
- 50. Заключение
- 51. Пребудет вечной истина, как
Слайд 2
Одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного
Теорема Пифагора
Слайд 3Содержание
Теорема Пифагора
Формулировки
История теоремы
Доказательства теоремы
Применение
Заключение
Слайд 4.
У Евклида эта теорема гласит: "В прямоугольном треугольнике квадрат стороны, натянутой
Латинский перевод арабского текста Аннаирици (около 900 г. до н. э. ), сделанный Герхардом Клемонским (начало 12 в.), в переводе на русский гласит: "Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол".
В Geometria Culmonensis (около 1400 г.) в переводе теорема читается так : "Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу".
В первом русском переводе евклидовых "Начал", сделанном Ф. И. Петрушевским, теорема Пифагора изложена так: "В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол".
Слайд 5
История теоремы
В древнем Китае особое внимание
Слайд 6
История теоремы
3 ² + 4 ² = 5²
было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея).
По мнению Кантора гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Слайд 7 Способ построения
Возьмем веревку
Слайд 8
История теоремы
У вавилонян приводится
Слайд 9
История теоремы
Геометрия у индусов,
была тесно связана с культом. Весьма вероятно,
что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э.
Слайд 11 Биография Пифагора
Великий ученый Пифагор родился около 570 г. до
Слайд 12 Жизнь Пифагора
Пифагор решается на сухопутное
Слайд 13
Школа Пифагора
Число
Слайд 14
Открытия Пифагорейцев
Теорема о сумме внутренних углов треугольника;
Построение правильных многоугольников и
3. Геометрические способы решения квадратных уравнений;
4. Деление чисел на четные и нечетные, простые и составные;
5. Введение фигурных, совершенных и дружественных чисел;
6. Доказательство того, что корень из двух не является рациональным числом;
7. Создание математической теории музыки и учения об арифметической геометрии и гармонических пропорциях и др.
Слайд 15 ...Прошло 20 лет. Слава о братстве разнеслась по всему миру.
Жизнь Пифагора
Слайд 16
Если дан нам треугольник
И притом с прямым углом
То квадрат гипотенузы
Катеты в квадрат возводим,
Сумму степеней находим
И таким простым путём
К результату мы придём.
Слайд 17 Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме
a2+b2 =c2
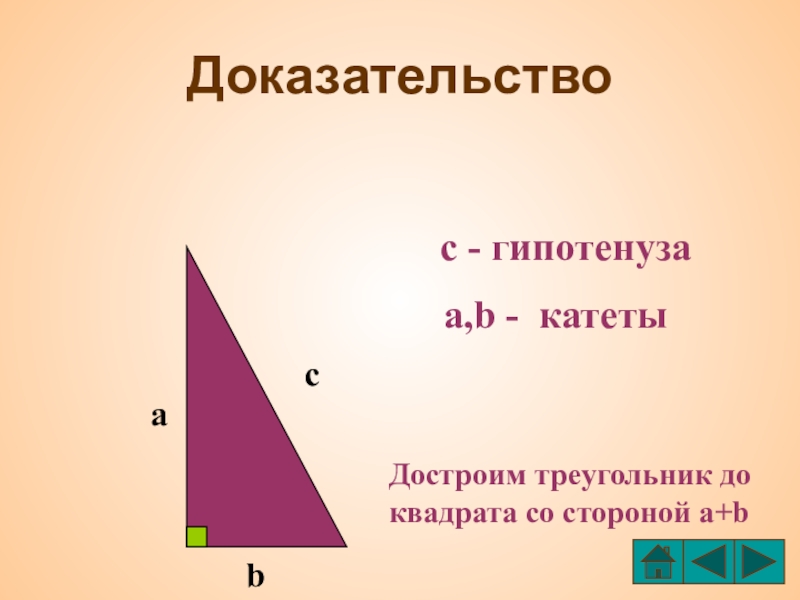
Слайд 18Доказательство
с - гипотенуза
a,b - катеты
a
b
c
Достроим
Слайд 19
Площадь
S=4ab/2ab+c2=2ab+c
Таким образом
Откуда,
С другой стороны, этот квадрат составлен из четырёх равных прямоугольных треугольников, площадь
каждого из которых равна
(a+b)2
(a+b)2 =2ab+c2
с2=a2+b2
a
b
b
a
b
a
b
a
c
c
c
c
Доказательство
Слайд 20 Обратная теорема
Если квадрат одной стороны
Слайд 21 Доказательство
Пусть в треугольнике АВС АВ2=АС2+ВС2.Докажем, что угол С прямой.
Рассмотрим
Но АС2+ВС2=АВ2 по условию теоремы. Следовательно (А1В1)2=АВ2, откуда А1В1=АВ. Треугольники АВС и А1В1С1 равны по трём сторонам, поэтому угол С равен углу С1, т.е. треугольник АВС прямоугольный с прямым углом С. Теорема доказана.
Слайд 22
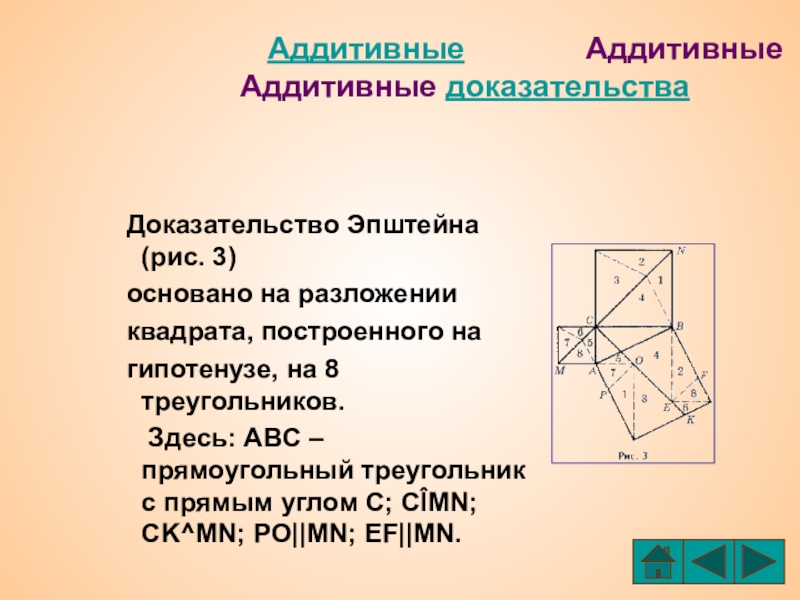
Доказательство Эпштейна (рис. 3)
основано на разложении
квадрата, построенного на
гипотенузе, на 8 треугольников.
Здесь: ABC – прямоугольный треугольник с прямым углом C; CÎMN; CK^MN; PO||MN; EF||MN.
Слайд 23Эти доказательства основаны на разложении квадратов, построенных на катетах, на фигуры,
Слайд 24 Аддитивные доказательства
На
Слайд 25 Аддитивные доказательства
Еще
Это разложение квадратов интересно тем, что его попарно равные четырехугольники могут быть отображены друг на друга параллельным переносом. Может быть предложено много и других доказательств теоремы Пифагора с помощью разложения квадратов на фигуры.
Слайд 26 Доказательства методом построения
К квадратам,
На рис. 7 к обычной Пифагоровой фигуре присоединены треугольники 1 и 2, равные исходному прямоугольному треугольнику.
Справедливость теоремы Пифагора вытекает из равновеликости шестиугольников AEDFPB и ACBNMQ. Здесь CÎEP, прямая EP делит шестиугольник AEDFPB на два равновеликих четырехугольника, прямая CM делит шестиугольник ACBNMQ на два равновеликих четырехугольника; поворот плоскости на 90° вокруг центра A отображает четырехугольник AEPB на четырехугольник ACMQ.
Слайд 27 Доказательства методом построения
На рис.
Разобьем этот прямоугольник на треугольники и прямоугольники. Из полученного прямоугольника вначале отнимем все многоугольники 1, 2, 3, 4, 5, 6, 7, 8, 9, остался квадрат, построенный на гипотенузе. Затем из того же прямоугольника отнимем прямоугольники 5, 6, 7 и заштрихованные прямоугольники, получим квадраты, построенные на катетах.
Слайд 28 Доказательства методом построения
Рис. 9
KLOA = ACPF = ACED = a2;
LGBO = CBMP = CBNQ = b2;
AKGB = AKLO + LGBO = c2;
отсюда c2 = a2 + b2
Слайд 29 Доказательства методом построения
Рис. 11 иллюстрирует еще
Слайд 30
Алгебраический метод доказательства
Слайд 31 Алгебраический метод доказательства
На рис. 13 ABC
Из того, что DABC подобен DACM следует
b2 = cb1; (1)
из того, что DABC подобен DBCM следует
a2 = ca1. (2)
Складывая почленно равенства (1) и (2), получим a2 + b2 = cb1 + ca1 = c(b1 + a1) = c2.
Если Пифагор действительно предложил такое доказательство, то он был знаком и с целым рядом важных геометрических теорем, которые современные историки математики обычно приписывают Евклиду.
Слайд 32 Доказательства методом дополнения
На рис. к
Слайд 33 Доказательство методом вычитания
1) треугольники 1, 2, 3, 4; 2) прямоугольник 5; 3) прямоугольник 6 и квадрат 8; 4) прямоугольник 7 и квадрат 9;
Затем выбросим из прямоугольника части так, чтобы остались только квадраты, построенные на катетах. Этими частями будут:
1) прямоугольники 6 и 7; 2) прямоугольник 5; 3) прямоугольник 1(заштрихован); 4) прямоугольник 2(заштрихован);
Осталось лишь показать, что отнятые части равновелики. Это легко видеть в силу расположения фигур. Из рисунка ясно, что:
1) прямоугольник 5 равновелик самому себе; четыре треугольника 1,2,3,4 равновелики двум прямоугольникам 6 и 7; прямоугольник 6 и квадрат 8, взятые вместе, равновелики прямоугольнику 1 (заштрихован);; прямоугольник 7 вместе с квадратом 9 равновелики прямоугольнику 2(заштрихован);
Слайд 34
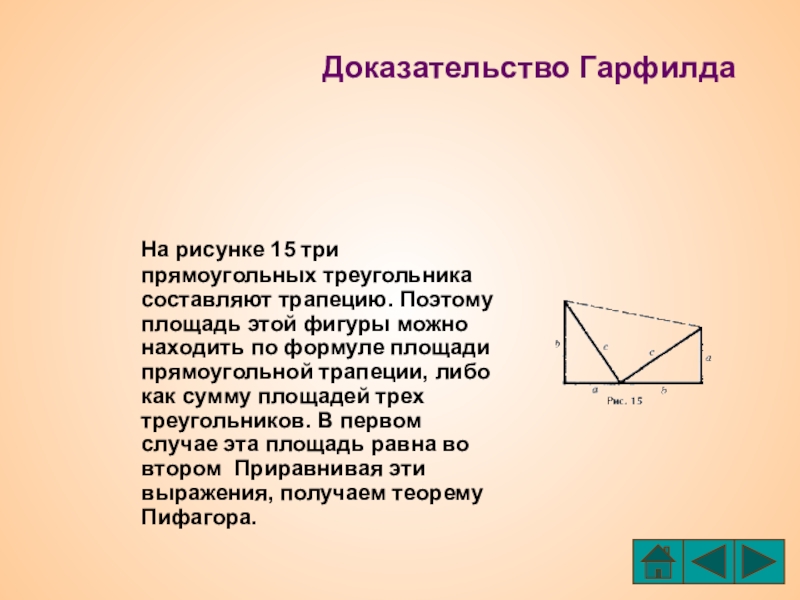
Доказательство Гарфилда
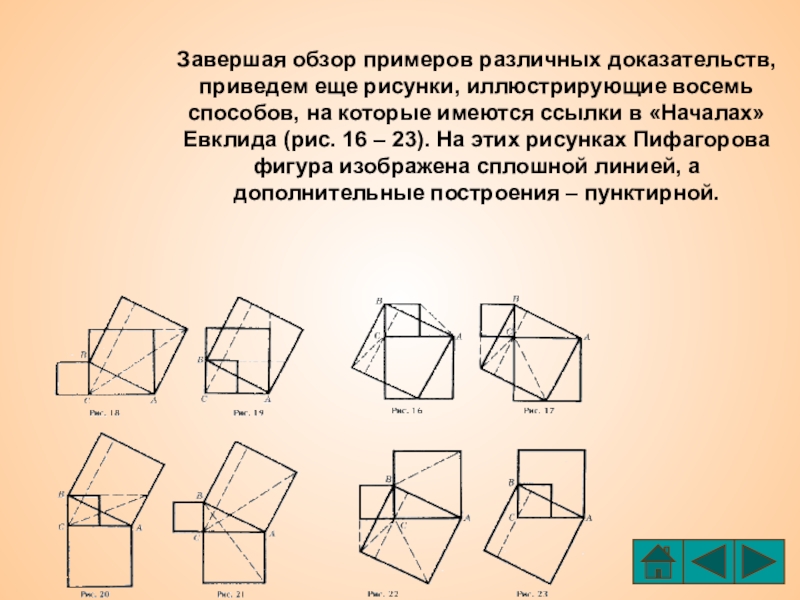
Слайд 35Завершая обзор примеров различных доказательств, приведем еще рисунки, иллюстрирующие восемь способов,
Слайд 36 Как уже было сказано выше, древние египтяне более 2000 лет
Слайд 37 Докажем, что этот треугольник прямоугольный. Построим прямоугольный треугольник
Сравнивая соотношения (3) и (4), получаем, что
c12 = c2, или c1 = c.
Таким образом, треугольники – данный и построенный – равны, так как имеют по три соответственно равные стороны. Угол C1 прямой, поэтому и угол C данного треугольника тоже прямой.
Слайд 38 Доказательство
На рисунке квадраты, построенные на катетах, размещены ступенями один рядом с другим. Эту фигуру, которая встречается в доказательствах, датируемых не позднее, чем 9 столетием н. э., индусы называли "стулом невесты". Общая часть двух квадратов, построенных на катетах, и квадрата, построенного на гипотенузе, - неправильный заштрихованный пятиугольник 5. Присоединив к нему треугольники 1 и 2, получим оба квадрата, построенные на катетах; если же заменить треугольники 1 и 2 равными им треугольниками 3 и 4, то получим квадрат, построенный на гипотенузе. На рисунках ниже изображены два различных расположения близких к тому, которое дается на первом рисунке.
Слайд 39 Доказательство Евклида
На гипотенузе и катетах прямоугольного треугольника АВС строятся соответствующие квадраты и доказывается, что прямоугольник BJLD равновелик квадрату ABFH, а прямоугольник ICEL - квадрату АСКС. Тогда сумма квадратов на катетах будет равна квадрату на гипотенузе. В самом деле, треугольники ABD и BFC равны по двум сторонам и углу между ними:
FB = AB, BC = BD; РFBC = d + РABC = РABD
Но SABD = 1/2 S BJLD, так как у треугольника ABD и прямоугольника BJLD общее основание BD и общая высота LD. Аналогично SFBC=1\2S ABFH . (BF-общее основание, АВ- общая высота). Отсюда, учитывая, что SABD=SFBC, имеем SBJLD=SABFH. Аналогично, используя равенство треугольников ВСК и АСЕ, доказывается, что SJCEL=SACKG.
Итак, SABFH+SACKG= SBJLD+SJCEL= SBCED.
Слайд 40 Упрощенное доказательство Евклида
Как в доказательствах
Слайд 41 Доказательство основанное на теории
В прямоугольном треугольника АВС проведем из вершины прямого угла высоту CD; тогда треугольник разобьется на два треугольника, также являющихся прямоугольными. Полученные треугольники будут подобны друг другу и исходному треугольнику. Это легко доказать, пользуясь первым признаком подобия(по двум углам). В самом деле, сразу видно что, кроме прямого угла, треугольники АВС и ACD имеют общий угол a, треугольники CBD и АВС - общий угол b. То, что малые треугольники также подобны друг другу, следует из того, что каждый из них подобен большому треугольнику. Впрочем, это можно установить и непосредственно.
Слайд 42 Доказательство индийского математика
Доказательство изображено на рисунке В пояснение к нему он написал только одну строчку: "Смотри!". Ученые считают, что он выражал площадь квадрата ,построенного на гипотенузе, как сумму площадей треугольников (4ab/2) и площадь квадрата (a-b)². Следовательно:
c²=4ab/2+(a-b)²
c=2ab+a²-2ab+b²
c²=a²+b²
Теорема доказана.
Слайд 43 Векторное доказательство
Пусть
Слайд 44 Применение теоремы
Область применения теоремы достаточно обширна и вообще не может быть указана с достаточной полнотой. Определим возможности, которые дает теорема Пифагора для вычисления длин отрезков некоторых фигур на плоскости. Диагональ d квадрата со стороной а можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а. Таким образом, d=2a, откуда: d²=2a².
Диагональ d прямоугольника со сторонами а и b вычисляется подобно тому, как вычисляется гипотенуза прямоугольного треугольника с катетами a и b. Мы имеем d²=a²+b²
Слайд 45 Применение теоремы
Пифагора
Таким образом имеем a = h +(a/2),
или h=(3/4)a. Отсюда вытекает ???h=1/2 3a.
Слайд 46 Применение теоремы
Возможности применения теоремы Пифагора к вычислениям не ограничиваются планиметрией. На рисунке изображен куб, внутри которого проведена диагональ d, являющаяся одновременно гипотенузой прямоугольного треугольника, заштрихованного на рисунке. Катетами треугольника служат рабро куба и диагональ квадрата, лежащего в основании (как указывалось ранее, длина диагонали равна 2а). Отсюда имеем d=a+(2a), d=3a, d=3a.
Рассуждение, подобное этому, можно провести и для прямоугольного параллелепипеда с ребрами a, b, с и получить для диагонали выражение d = a + b + c.
Слайд 47 Применение теоремы
Исследуем пирамиду, например, такую, в основании которой лежит квадрат и высота которой проходит через центр этого квадрата (правильную пирамиду). Пусть сторона квадрата - а, и высота пирамиды - h. Найдем s (длину боковых ребер пирамиды).
Ребра будут гипотенузами прямоугольных треугольников, у которых один из катетов - высота h, а другой - половина диагонали квадрата ???(1/2*2a). Вследствие этого имеем: S =h+(1/2)a.
Затем можем вычислить высоту h1 боковых граней.
h1= h+(1/4)a.
Слайд 48 Применение теоремы
Пифагора
или b2/16+ bp/2+p2=b2/16+b2/4-bp+p2, откуда bp/2=b/4-bp. Разделив на b и приводя подобные члены, получим: (3/2)p=b/4, p=b/6.
Слайд 49 Заключение
В настоящее время известно,
что эта теорема не была открыта Пифагором. Однако одни полагают, что Пифагор первым дал ее полноценное доказательство, а другие отказывают ему и в этой заслуге. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих "Начал". С другой стороны, Прокл утверждает, что доказательство в "Началах" принадлежит самому Евклиду.
Слайд 50 Заключение
Причина такой популярности теоремы
Слайд 51 Пребудет вечной истина, как скоро Ее познает слабый человек! И