- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Свойства равнобедренного треугольника(7 класс)
Содержание
- 1. Презентация по геометрии на тему Свойства равнобедренного треугольника(7 класс)
- 2. ABCТреугольник называется равнобедренным, если две его стороны равны
- 3. АВСАВ, ВС - боковые стороны равнобедренного треугольникаА,
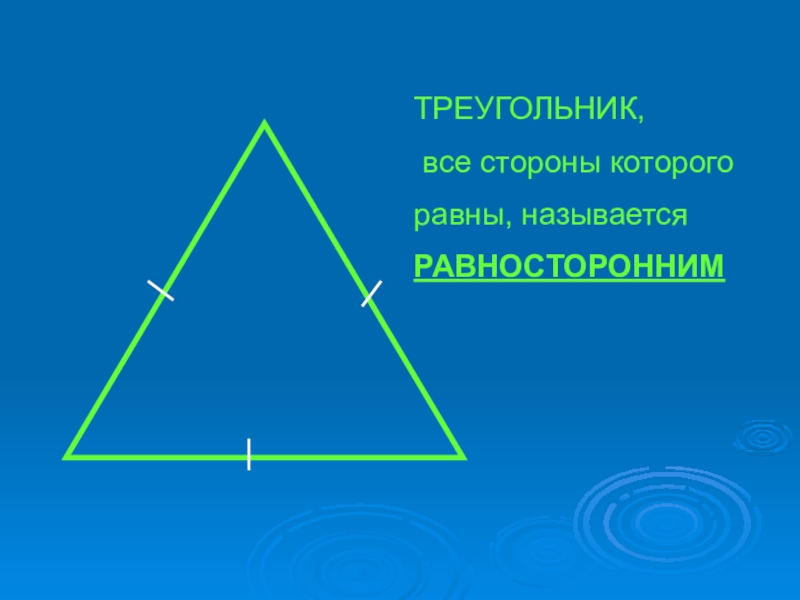
- 4. ТРЕУГОЛЬНИК, все стороны которого равны, называется РАВНОСТОРОННИМ
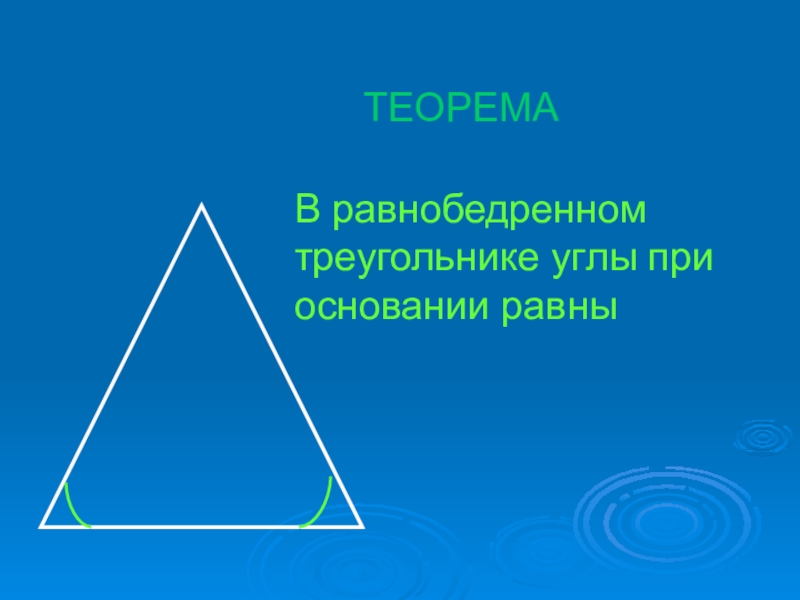
- 5. В равнобедренном треугольнике углы при основании равныТЕОРЕМА
- 6. АВСДАНО: АВС – равнобедренный, АС – основание.ДОКАЗАТЬ:
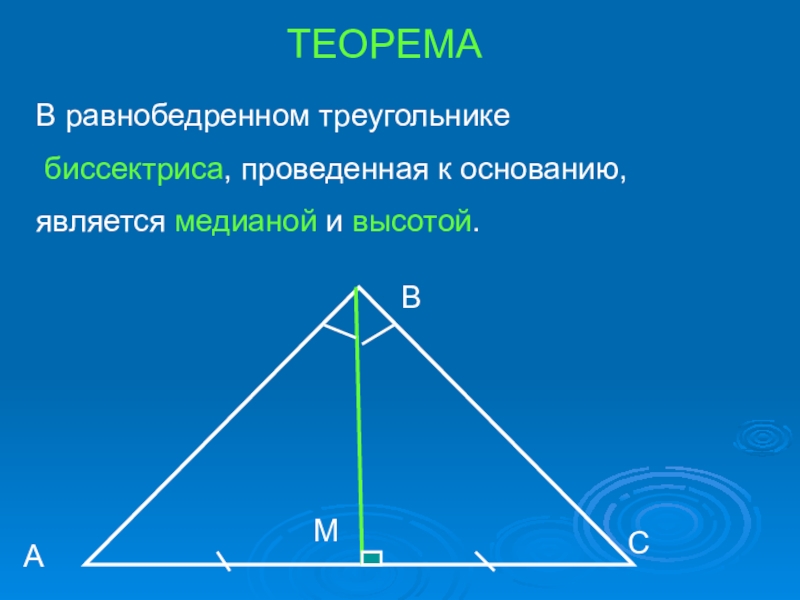
- 7. ТЕОРЕМАВ равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.АВСМ
ABCТреугольник называется равнобедренным, если две его стороны равны
Слайд 3
А
В
С
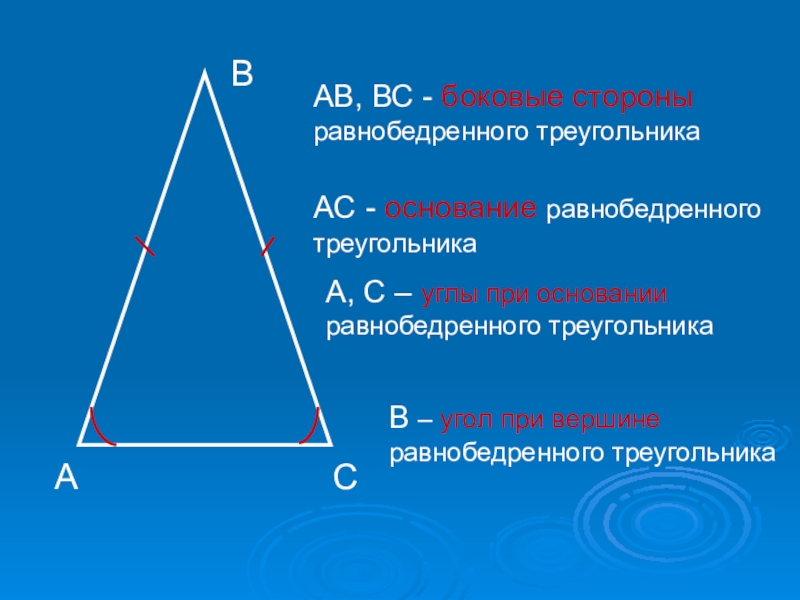
АВ, ВС - боковые стороны равнобедренного треугольника
А, С – углы при
основании равнобедренного треугольника
АС - основание равнобедренного треугольника
В – угол при вершине равнобедренного треугольника
Слайд 6
А
В
С
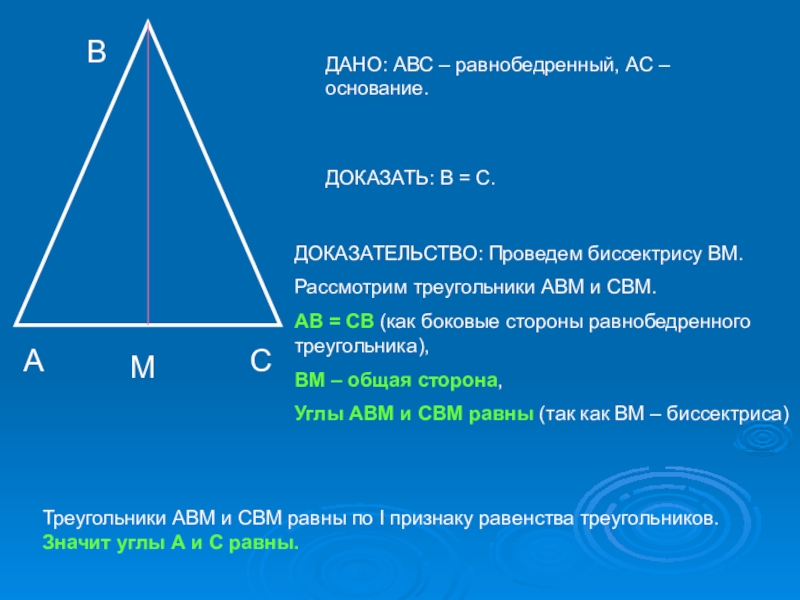
ДАНО: АВС – равнобедренный, АС – основание.
ДОКАЗАТЬ: В = С.
ДОКАЗАТЕЛЬСТВО: Проведем
биссектрису ВМ.
Рассмотрим треугольники АВМ и СВМ.
АВ = СВ (как боковые стороны равнобедренного треугольника),
ВМ – общая сторона,
Углы АВМ и СВМ равны (так как ВМ – биссектриса)
Рассмотрим треугольники АВМ и СВМ.
АВ = СВ (как боковые стороны равнобедренного треугольника),
ВМ – общая сторона,
Углы АВМ и СВМ равны (так как ВМ – биссектриса)
М
Треугольники АВМ и СВМ равны по I признаку равенства треугольников. Значит углы А и С равны.