учитель математики
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Сумма углов треугольника(7 класс)
Содержание
- 1. Презентация по геометрии на тему Сумма углов треугольника(7 класс)
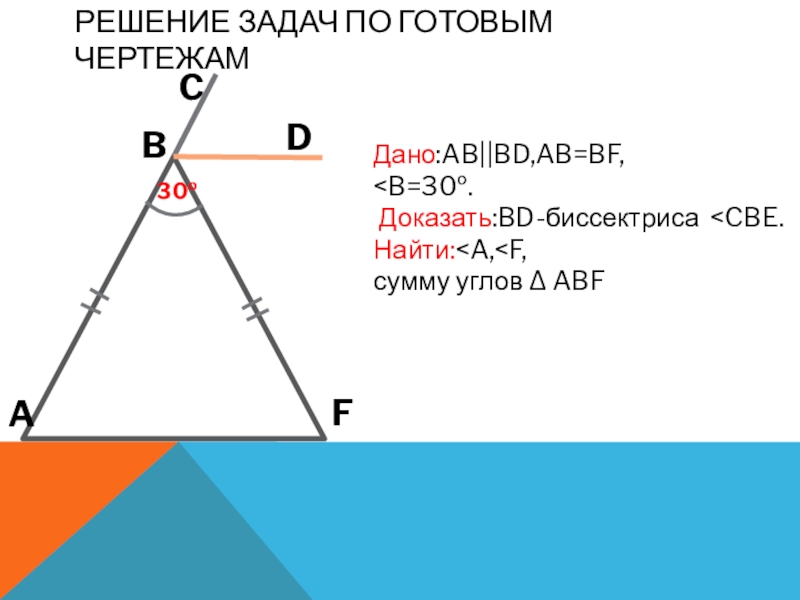
- 2. Решение задач по готовым чертежамДано:AB||BD,AB=BF,
- 3. Дано:DE||AC,Найти: сумму углов ΔABCРешение задач по готовым чертежамABCDE
- 4. Сумма углов
- 5. Слайд 5
- 6. Внешний угол треугольникаоПРЕДЕЛЕНИЕВнешним
- 7. Внешний угол треугольника равен сумме двух углов
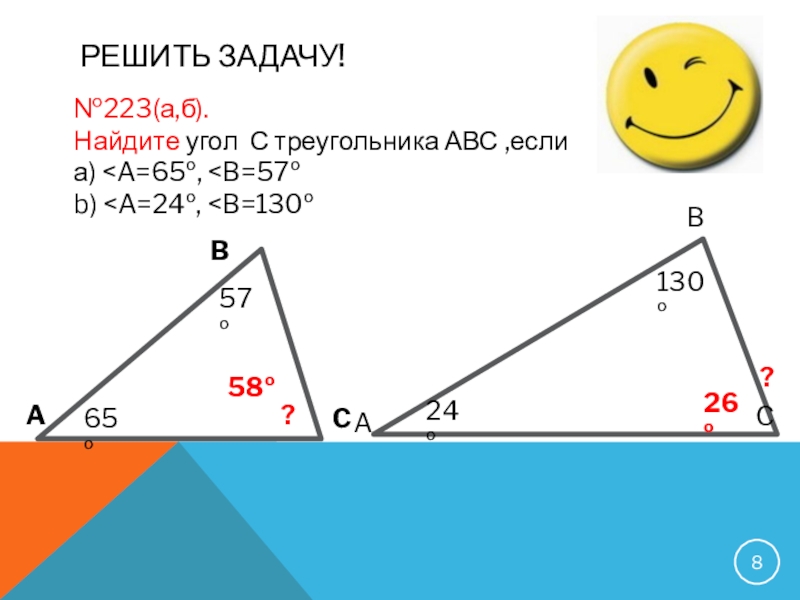
- 8. Решить задачу!№223(а,б).Найдите угол С треугольника АВС ,если а)
- 9. Реши задачу! №226Докажите, что каждый угол равностороннего
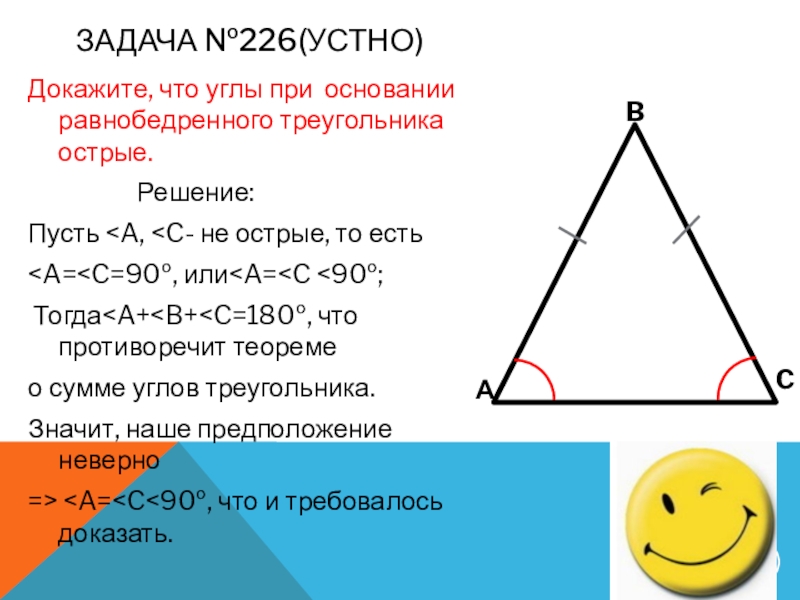
- 10. Задача №226(устно)Докажите, что углы при основании равнобедренного
- 11. Может ли треугольник иметь:Вывод: в любом треугольнике
- 12. Проверь себя
- 13. Прямоугольный треугольник Если один из углов треугольника прямой, то треугольник называют прямоугольным.КАТЕТАГИПОТЕНУЗАКАТЕТBC
- 14. Реши задачу!№227Найдите углы равнобедренного теугольника, если:а) угол
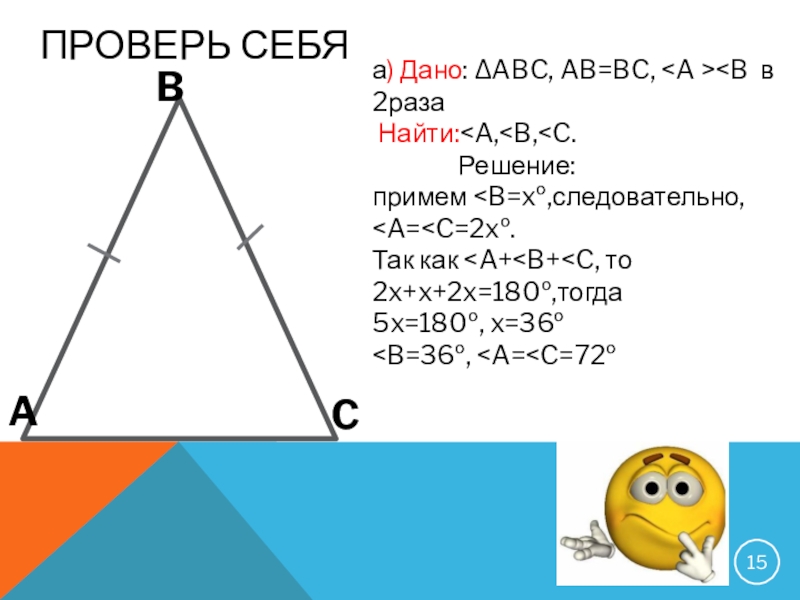
- 15. Проверь себяа) Дано: ΔABC, AB=BC,
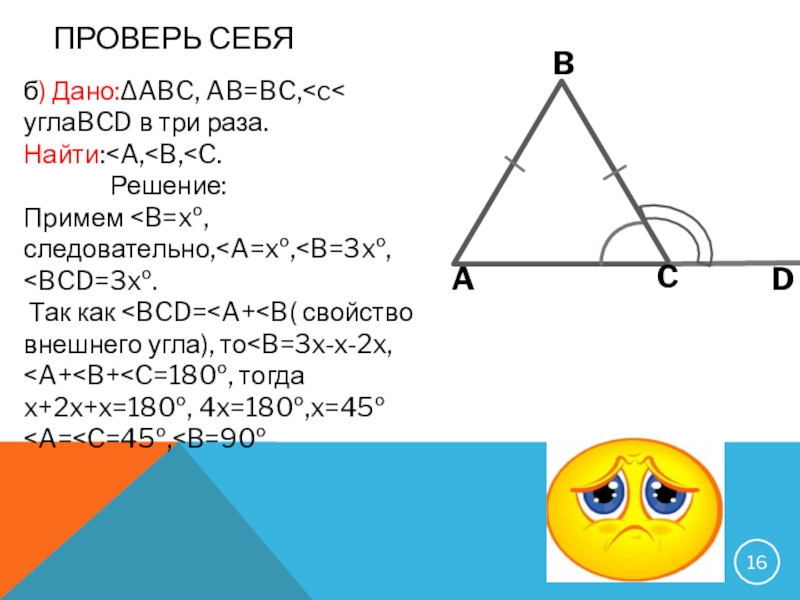
- 16. Проверь себяб) Дано:ΔABC, AB=BC,
- 17. Реши задачу!№ 224.Найдите угол С треугольника АВС, если
- 18. Проверь себяДано:ΔABC,
- 19. Реши задачу!№ 228Найдите углы равнобедренного треугольника, еслиодин из его углов равен:а)40º;б) 60º;в)100º.
- 20. Проверь себяРассмотрим два случая:А) Угол при основании
- 21. Проверь себя2) Опираемся на доказанное в задаче
- 22. Итог урокаЧто нового узнали на уроке?Составьте синквейн к уроку
- 23. Домашнее заданиеИзучить пункты 30-31;Ответить на вопросы1,2,3,4 на с.89.Решить задачи №223(в),№230
Решение задач по готовым чертежамДано:AB||BD,AB=BF,
Слайд 1Сумма углов треугольника
МБОУ»Ширинская «СОШ №18 ,Республика Хакасия.
Автор : Несивкина Галина Анатольевна,
Слайд 4 Сумма углов треугольника
Случайно ли сумма углов
Δ ABC оказалась равной 180º, или этим свойством обладает любой треугольник?
У каждого треугольника сумма углов равна 180º
Это утверждение носит название теоремы о сумме углов треугольника.
Итак, тема сегодняшнего урока
У каждого треугольника сумма углов равна 180º
Это утверждение носит название теоремы о сумме углов треугольника.
Итак, тема сегодняшнего урока
Слайд 5
Теорема
Сумма углов треугольника равна 180º
Доказательство:
2
3
1
4
5
A
B
C
а
Рассмотрим произвольный треугольник АВС и докажем, что
<1и <4-накрест лежащие
<3и<5-накрест лежащие
Поэтому <4=<1,<5=<3.(1)
<4+<2+<5=180º, учитывая (1)
<1+<2+<3=180º, или
Слайд 6 Внешний угол треугольника
оПРЕДЕЛЕНИЕ
Внешним углом треугольника называется угол,
смежный
с каким-нибудь углом этого треугольника
с каким-нибудь углом этого треугольника
4
1
2
Слайд 7Внешний угол треугольника равен сумме двух углов треугольника, не смежных с
ним.
Угол 4 –внешний угол, смежный с углом 3 данного треугольника. Так как <4+<3=180º, то <4=<1+<2,
что и требовалось доказать.
Следствие
3
Слайд 9Реши задачу!
№226
Докажите, что каждый угол равностороннего треугольника равен 60º.
Решение.
Так как AB=BC=AC,
равнобедренного треугольника.
Так как
каждый угол равностороннегоΔ по 60º, что и требовалось доказать.
Так как AB=BC=AC,
Так как
каждый угол равностороннегоΔ по 60º, что и требовалось доказать.
A
B
C
Слайд 10Задача №226(устно)
Докажите, что углы при основании равнобедренного треугольника острые.
Решение:
Пусть Тогдао сумме углов треугольника.
Значит, наше предположение неверно
=>
Пусть
Значит, наше предположение неверно
=>
А
B
C
Слайд 11Может ли треугольник иметь:
Вывод:
в любом треугольнике либо
все три угла острые,
либо два угла острые, а -третий -тупой или прямой.
-два прямых угла
-два тупых угла
-один прямой и один тупой угол?
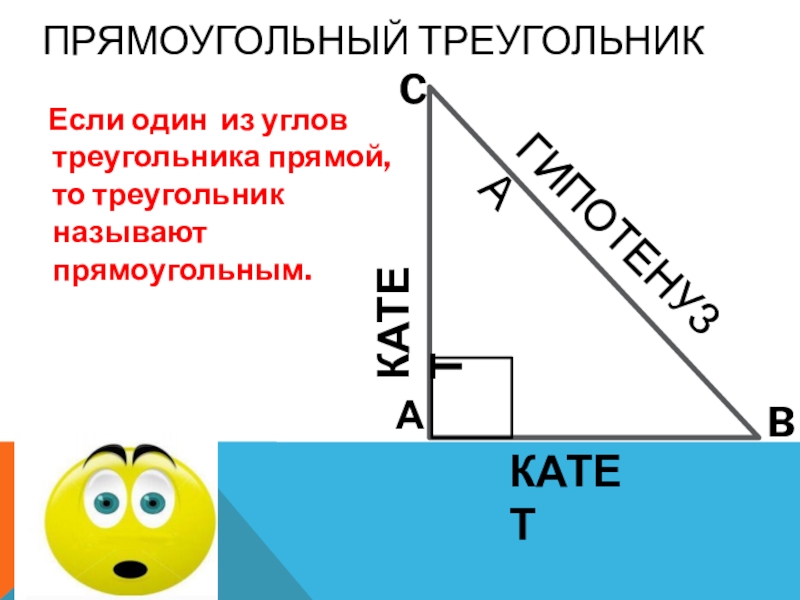
Слайд 13Прямоугольный треугольник
Если один из углов треугольника прямой, то треугольник
называют прямоугольным.
КАТЕТ
А
ГИПОТЕНУЗА
КАТЕТ
B
C
Слайд 14Реши задачу!
№227
Найдите углы равнобедренного теугольника, если:
а) угол при основании в два
раза больше угла, противолежащего основанию;
б)угол при основании в три раза меньше внешнего угла, смежного с ним.
б)угол при основании в три раза меньше внешнего угла, смежного с ним.
Слайд 18Проверь себя
Дано:ΔABC,
Решение:
Примем 1 часть -хº, следовательно,Так как 2x+3x+4x, =180º,
тогда 9x=180º
X=20º
20º приходиться на 1 часть.
<2*20º=40º,Ответ:40º,60º,80º
Примем 1 часть -хº, следовательно,
тогда 9x=180º
X=20º
20º приходиться на 1 часть.
<2*20º=40º,
А
B
C
Слайд 19Реши задачу!
№ 228
Найдите углы равнобедренного треугольника, если
один из его углов равен:
а)40º;
б)
60º;
в)100º.
в)100º.
Слайд 20Проверь себя
Рассмотрим два случая:
А) Угол при основании равен 40º, тогда второй
угол при основании
Равнобедренного треугольника тоже равен 40º; значит, угол при вершине
Равен 180º-(40º+40º)=100º.
Б) Угол при вершине равен 40º, тогда углы при основании равны
(180º-100º):2=70º.
Ответ: 40º,40º,100º или 40º,70º, 70º.
Равнобедренного треугольника тоже равен 40º; значит, угол при вершине
Равен 180º-(40º+40º)=100º.
Б) Угол при вершине равен 40º, тогда углы при основании равны
(180º-100º):2=70º.
Ответ: 40º,40º,100º или 40º,70º, 70º.
Слайд 21Проверь себя
2) Опираемся на доказанное в задаче № 226 утверждение: углы
при основании
равнобедренного треугольника острые.
Значит угол при вершине равен100º, а углы при основании равны(180º-100º):2=40º
Ответ:100º,40º и 40º.
равнобедренного треугольника острые.
Значит угол при вершине равен100º, а углы при основании равны(180º-100º):2=40º
Ответ:100º,40º и 40º.
Слайд 23Домашнее задание
Изучить пункты 30-31;
Ответить на вопросы1,2,3,4 на с.89.
Решить задачи №223(в),№230
