- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему РОМБ
Содержание
- 1. Презентация по геометрии на тему РОМБ
- 2. Понятие ромба Ромб (греч. rhombus)Ромбом называется параллелограмм,
- 3. СвойстваРомб является параллелограммом.Его противолежащие стороны попарно параллельны,
- 4. Теорема: Диагонали ромба взаимно перпендикулярны и делят
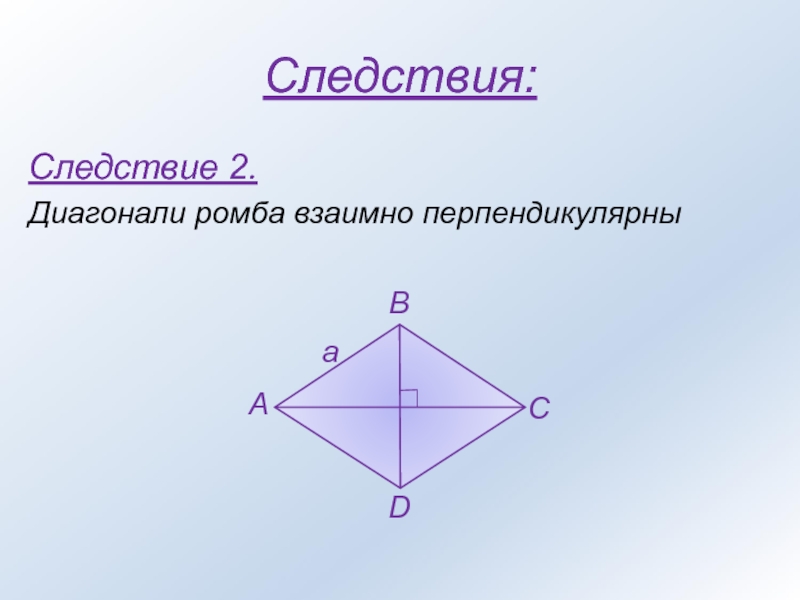
- 5. Следствия:Следствие 2. Диагонали ромба взаимно перпендикулярны
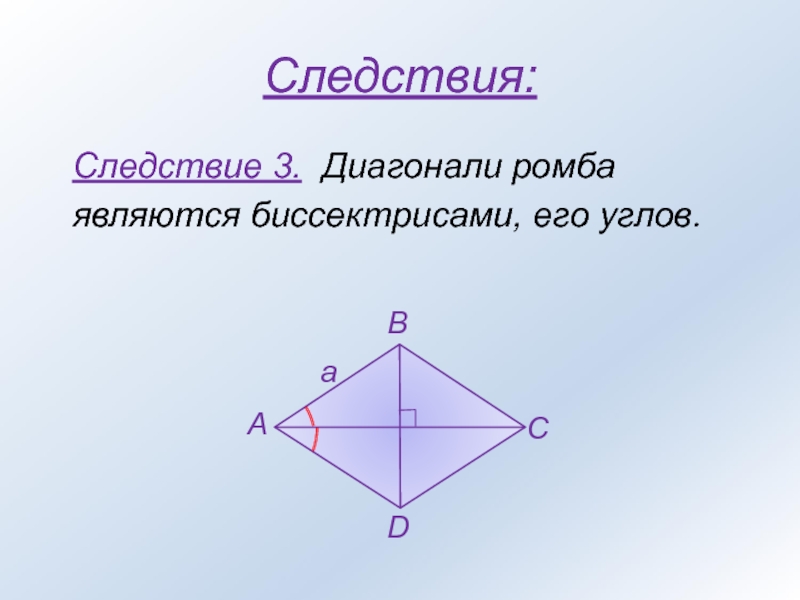
- 6. Следствия:Следствие 3. Диагонали ромба являются биссектрисами, его углов.
- 7. Площадь ромба:Площадь ромба равна половине произведения его диагоналей:
- 8. Площадь ромбаПлощадь ромба равна половине произведения его
- 9. Периметр ромбаПериметр ромба равен сумме всех его
Понятие ромба Ромб (греч. rhombus)Ромбом называется параллелограмм, у которого все стороны равны. Обладает всеми свойствами параллелограмма.Ромб с прямыми углами называется квадратом.
Слайд 2Понятие ромба
Ромб (греч. rhombus)
Ромбом называется параллелограмм, у которого все стороны
равны.
Обладает всеми свойствами параллелограмма.
Ромб с прямыми углами называется квадратом.
Обладает всеми свойствами параллелограмма.
Ромб с прямыми углами называется квадратом.
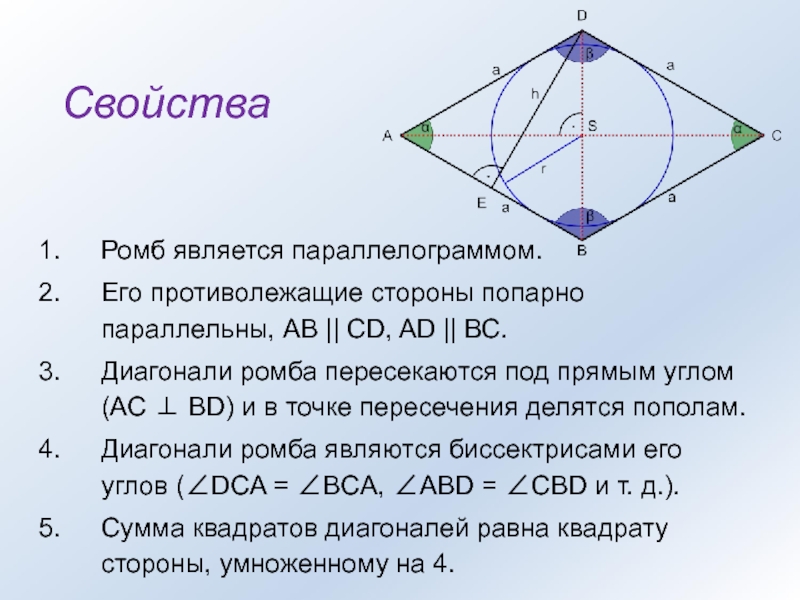
Слайд 3Свойства
Ромб является параллелограммом.
Его противолежащие стороны попарно параллельны, АВ || CD, AD
|| ВС.
Диагонали ромба пересекаются под прямым углом (AC BD) и в точке пересечения делятся пополам.
Диагонали ромба являются биссектрисами его углов (DCA = BCA, ABD = CBD и т. д.).
Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.
Диагонали ромба пересекаются под прямым углом (AC BD) и в точке пересечения делятся пополам.
Диагонали ромба являются биссектрисами его углов (DCA = BCA, ABD = CBD и т. д.).
Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.
Слайд 4Теорема: Диагонали ромба взаимно перпендикулярны и делят его углы пополам
Доказать, что:
АС BD; BAC= DAC
Доказательство: По определению ромба
АB = AD, поэтому треугольник BAD равнобедренный. Так как ромб - параллелограмм, то его диагонали точкой О пересечения делятся пополам. Следовательно, AO – медиана равнобедренного треугольника BAD, а значит, высота и биссектриса этого треугольника. Поэтому AC BD и BAC = DAC, ч.т.д.
Доказательство: По определению ромба
АB = AD, поэтому треугольник BAD равнобедренный. Так как ромб - параллелограмм, то его диагонали точкой О пересечения делятся пополам. Следовательно, AO – медиана равнобедренного треугольника BAD, а значит, высота и биссектриса этого треугольника. Поэтому AC BD и BAC = DAC, ч.т.д.
Слайд 8Площадь ромба
Площадь ромба равна половине произведения его диагоналей.
Поскольку ромб является параллелограммом,
его площадь также равна произведению его стороны на высоту.
Кроме того площадь ромба может быть вычислена по формуле, где – угол α между двумя смежными сторонами ромба.
Слайд 9Периметр ромба
Периметр ромба равен сумме всех его
четырех сторон. Формула периметра
ромба:
P = 4a, где a – сторона ромба
P = 4a, где a – сторона ромба