- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Преобразования плоскости. Движение и его свойства. Симметрия относительно точки.
Содержание
- 1. Презентация по геометрии на тему Преобразования плоскости. Движение и его свойства. Симметрия относительно точки.
- 2. Фигура – это множество точек плоскости.Геометрические фигуры
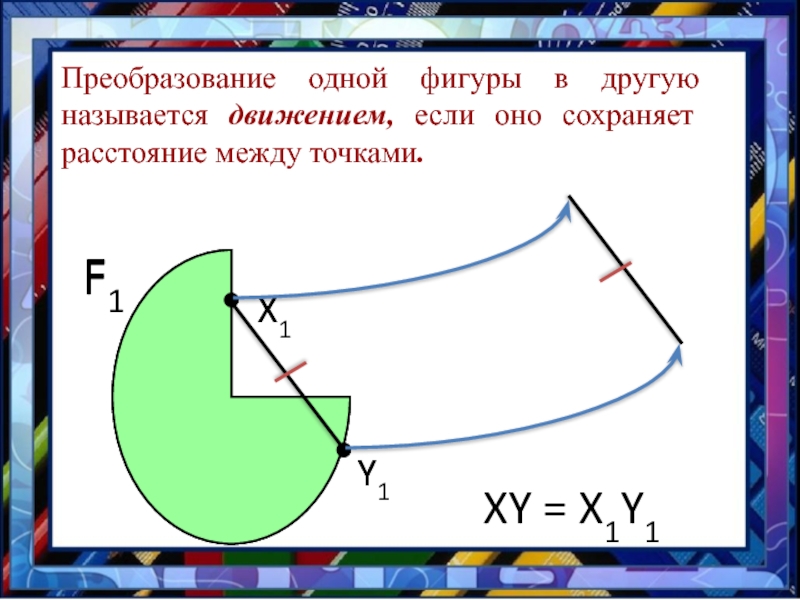
- 3. Преобразование одной фигуры в другую называется движением, если оно сохраняет расстояние между точками. Y1XY = X1Y1
- 4. Слайд 4
- 5. Слайд 5
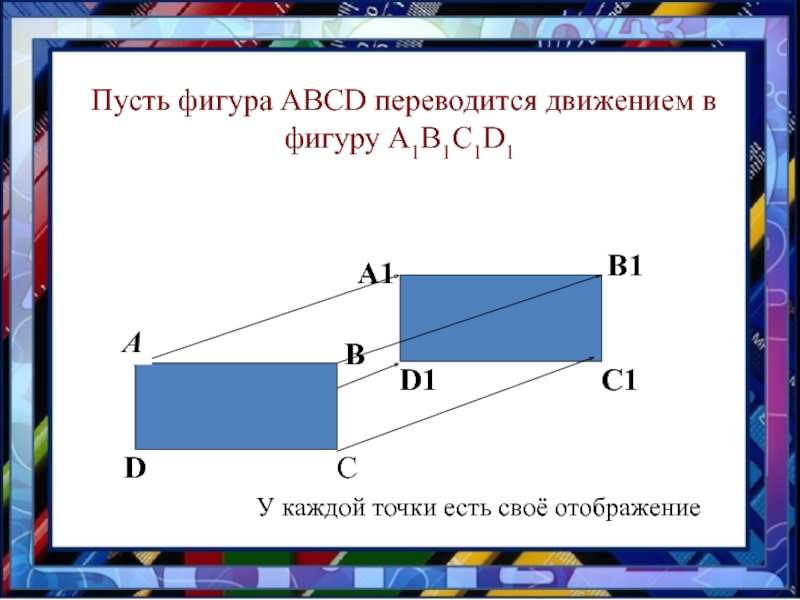
- 6. Пусть фигура АВСD переводится движением в фигуру А1В1С1D1АВСDА1В1С1D1У каждой точки есть своё отображение
- 7. Свойства движения При движении: - прямые переходят
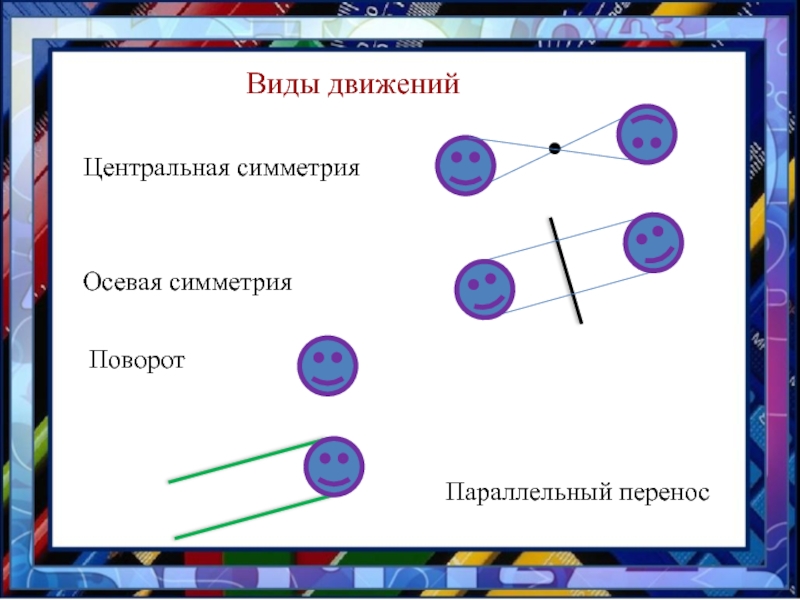
- 8. Осевая симметрияЦентральная симметрияПоворотПараллельный переносВиды движений
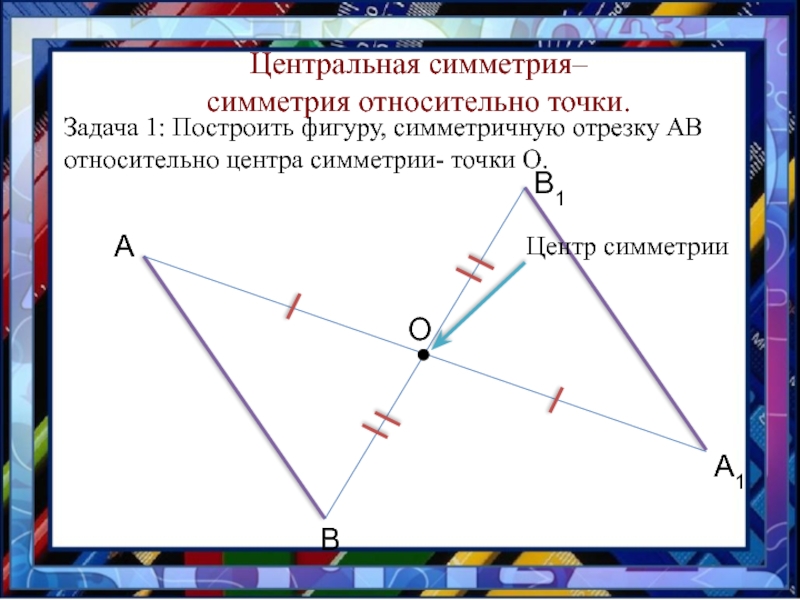
- 9. А1АВВ1ОЦентральная симметрия– симметрия относительно точки.Задача 1: Построить фигуру, симметричную отрезку АВ относительно центра симметрии- точки О.
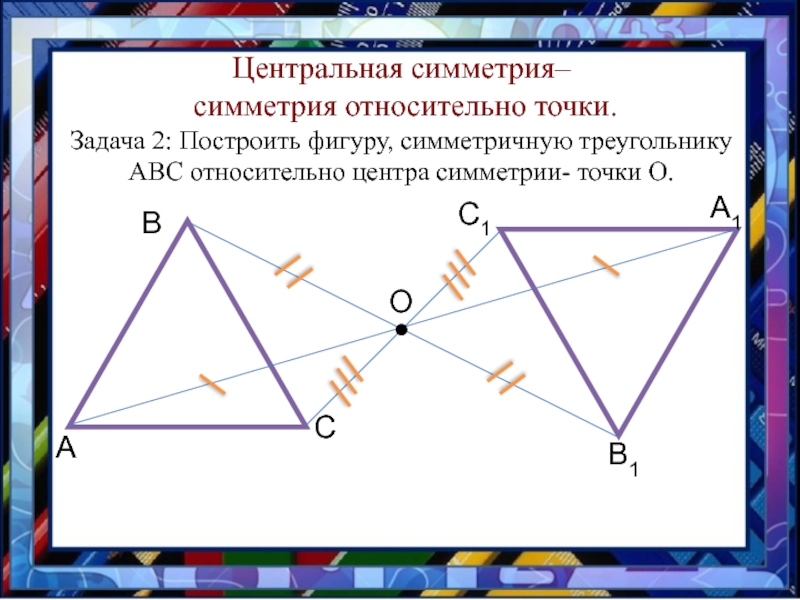
- 10. ОА1В1С1Центральная симметрия– симметрия относительно точки. Задача 2:
- 11. Вывод: Чтобы построить фигуру, симметричную данной относительно
- 12. Домашнее задание: Контрольные вопросы 1-6, стр.115-118 пункты
- 13. Преобразования плоскости.Движение и его свойства. Симметрия относительно
Фигура – это множество точек плоскости.Геометрические фигуры можно не только рассматривать, измерять и изучать их свойства. Над ними можно совершать различные преобразования. Преобразование плоскости –это взаимно однозначное соответствие, отображающее плоскость на себя.
Слайд 2Фигура – это множество точек плоскости.
Геометрические фигуры можно не только рассматривать,
измерять и изучать их свойства. Над ними можно совершать различные преобразования.
Преобразование плоскости –это взаимно однозначное соответствие, отображающее плоскость на себя.
Преобразование плоскости –это взаимно однозначное соответствие, отображающее плоскость на себя.
Слайд 3Преобразование одной фигуры в другую называется движением, если оно сохраняет расстояние
между точками.
Y1
XY = X1Y1
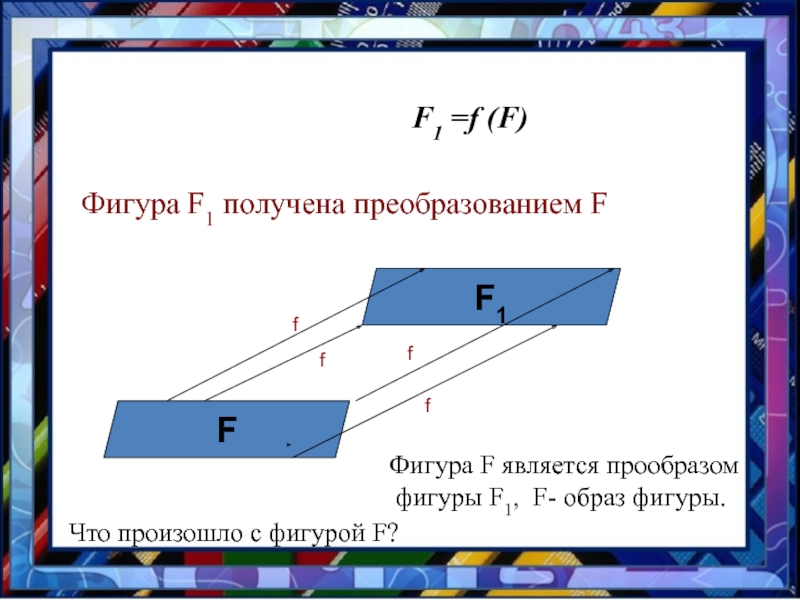
Слайд 4 F1 =f
(F)
Фигура F1 получена преобразованием F
F
F1
Фигура F является прообразом
фигуры F1, F- образ фигуры.
f
f
f
f
Что произошло с фигурой F?
Слайд 5 Движение
Преобразование одной
фигуры в другую называется ДВИЖЕНИЕМ, если оно сохраняет расстояние между точками, т.е. переводит любые две точки Х и У одной фигуры в точки Х1 и У1 другой фигуры так, что ХУ = Х1 У1
Слайд 6 Пусть фигура АВСD переводится движением в фигуру А1В1С1D1
А
В
С
D
А1
В1
С1
D1
У каждой точки
есть своё отображение
Слайд 7Свойства движения
При движении:
- прямые переходят в прямые
- полупрямые в
полупрямые
- отрезки в отрезки
- углы между полупрямыми сохраняются
- расстояния между точками сохраняется
- отрезки в отрезки
- углы между полупрямыми сохраняются
- расстояния между точками сохраняется
Слайд 9
А1
А
В
В1
О
Центральная симметрия–
симметрия относительно точки.
Задача 1: Построить фигуру, симметричную отрезку АВ
относительно центра симметрии- точки О.
Слайд 10О
А1
В1
С1
Центральная симметрия–
симметрия относительно точки.
Задача 2: Построить фигуру, симметричную треугольнику АВС
относительно центра симметрии- точки О.
Слайд 11Вывод: Чтобы построить фигуру, симметричную данной относительно точки О, нужно каждую
точку фигуры соединить с точкой О, продолжить полученный отрезок равным ему, отметить на конце этого отрезка образ исходной точки, затем соединить полученные образы .
Вопросы:
1. В какую фигуру переходит при движении квадрат? Объяснить ответ.
2. Доказать, что при движении параллелограмм переходит в параллелограмм.
Центральная симметрия–
симметрия относительно точки.
Слайд 12Домашнее задание:
Контрольные вопросы 1-6, стр.115-118 пункты 82-84, № 12(1), №13(1)
Задачи
на повторение:
1. Даны точки А (2; 0) и В (-2; 6). Составь уравнение окружности, диаметром которой является отрезок АВ.
2. Найди угловой коэффициент прямой х + 2у + 3 = 0 и точки пересечения её с осями координат.
3. Среди прямых, заданных уравнениями, укажи пары параллельных прямых: 1) х + у = 1; 2) у - х = 1; 3) х - у = 2; 4) y = 4; 5) у = 3; 6) 2х + 2у + 3 = 0.
1. Даны точки А (2; 0) и В (-2; 6). Составь уравнение окружности, диаметром которой является отрезок АВ.
2. Найди угловой коэффициент прямой х + 2у + 3 = 0 и точки пересечения её с осями координат.
3. Среди прямых, заданных уравнениями, укажи пары параллельных прямых: 1) х + у = 1; 2) у - х = 1; 3) х - у = 2; 4) y = 4; 5) у = 3; 6) 2х + 2у + 3 = 0.
Слайд 13Преобразования плоскости.
Движение и его свойства.
Симметрия относительно точки.
Автор шаблона и презентации
Конева Н. А, учитель математики
МБОУ БГО СОШ №4
1