другого и соответствующие стороны пропорциональны. Коэффициент пропорциональности называется коэффициентом подобия.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Первый признак равенства треугольников
Содержание
- 1. Презентация по геометрии на тему Первый признак равенства треугольников
- 2. Первый признак подобияТеорема. (Первый признак подобия.) Если
- 3. ПримерЧерез внешнюю точку E окружности проведены прямая,
- 4. Вопрос 1Какие треугольники называются подобными?Ответ: Два треугольника
- 5. Вопрос 2Сформулируйте первый признак подобия треугольников.Ответ: Если
- 6. Упражнение 1Подобны ли любые два: а) равносторонних
- 7. Упражнение 2Стороны треугольника равны 5 см, 8
- 8. Упражнение 3Подобны ли прямоугольные треугольники, если у
- 9. Упражнение 4Два треугольника подобны. Два угла одного
- 10. Упражнение 5В подобных треугольниках АВС и А1В1С1
- 11. Упражнение 6Ответ: AC = 4 м, B1C1 = 14 м.
- 12. Упражнение 7Стороны треугольника относятся как 5:3:7. Найдите
- 13. Упражнение 8На рисунке укажите все подобные треугольники.Ответ:
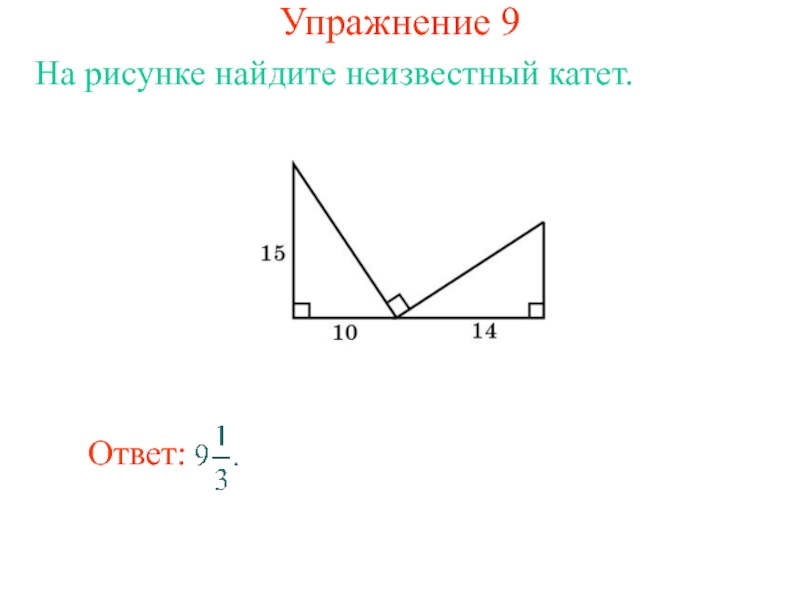
- 14. Упражнение 9На рисунке найдите неизвестный катет.
- 15. Упражнение 10У двух равнобедренных треугольников углы между
- 16. Упражнение 11Катеты одного прямоугольного треугольника на 3
- 17. Упражнение 12В треугольник со стороной а и
- 18. Упражнение 13В треугольник АВС вписан ромб ADEF
- 19. Упражнение 14Можно ли треугольник пересечь прямой, непараллельной
- 20. Упражнение 15Ответ: DEK и DLF, DEK и
- 21. Упражнение 16Ответ: ABH и ADC, ACH и
- 22. Упражнение 17Докажите, что в прямоугольном треугольнике перпендикуляр,
Первый признак подобияТеорема. (Первый признак подобия.) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
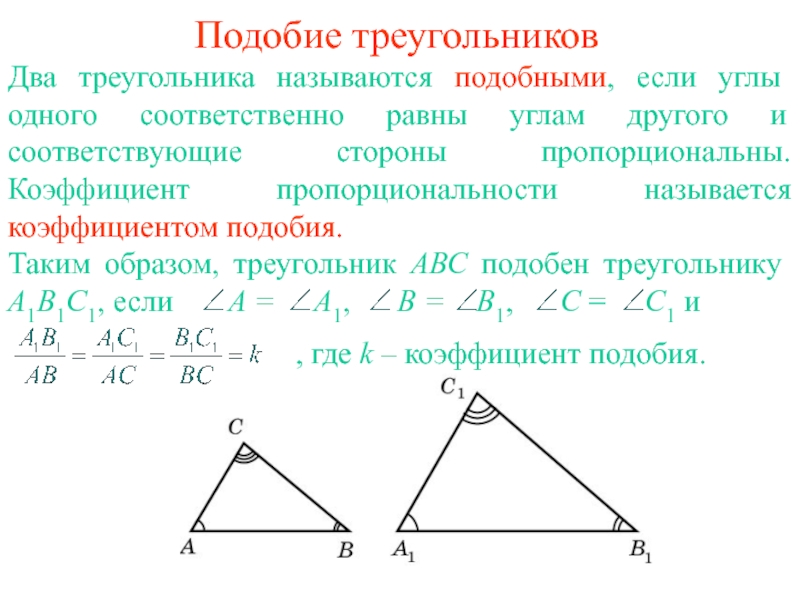
Слайд 1Подобие треугольников
Два треугольника называются подобными, если углы одного соответственно равны углам
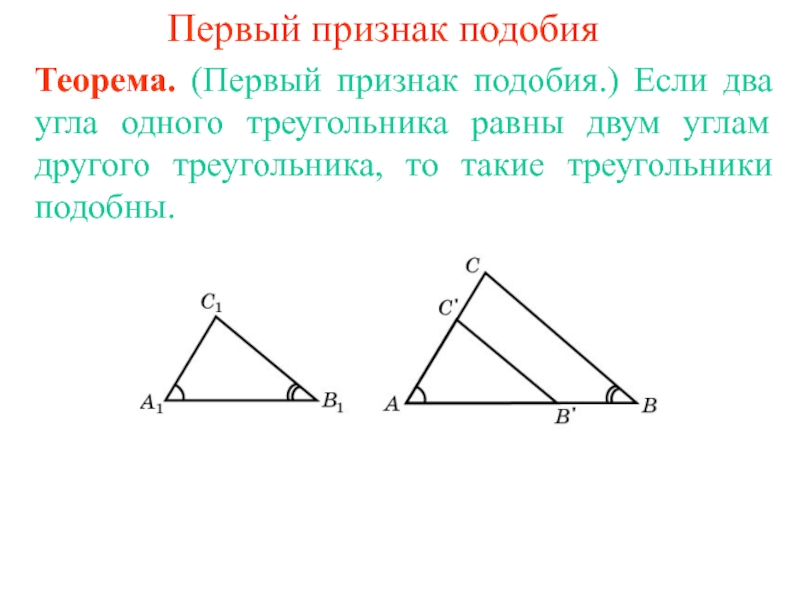
Слайд 2Первый признак подобия
Теорема. (Первый признак подобия.) Если два угла одного треугольника
равны двум углам другого треугольника, то такие треугольники подобны.
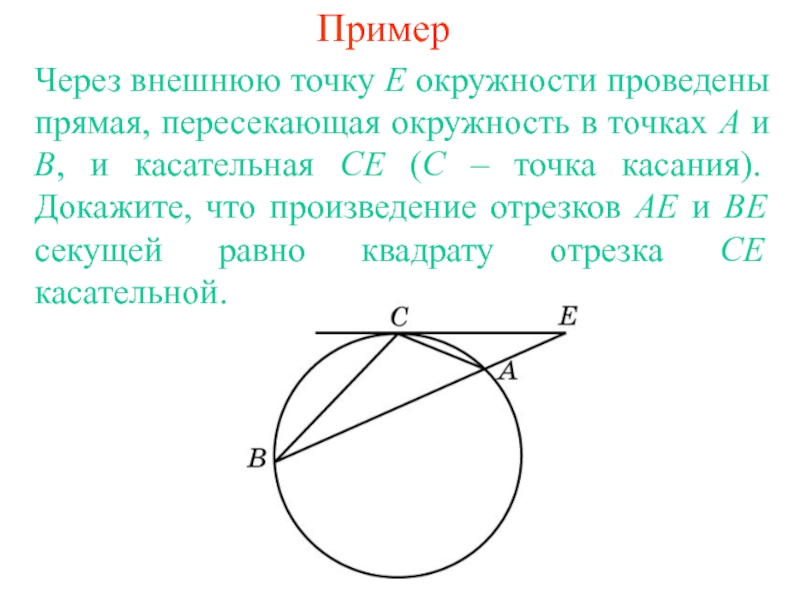
Слайд 3Пример
Через внешнюю точку E окружности проведены прямая, пересекающая окружность в точках
A и B, и касательная CE (C – точка касания). Докажите, что произведение отрезков AE и BE секущей равно квадрату отрезка CE касательной.
Слайд 4Вопрос 1
Какие треугольники называются подобными?
Ответ: Два треугольника называются подобными, если углы
одного соответственно равны углам другого и соответствующие стороны пропорциональны.
Слайд 5Вопрос 2
Сформулируйте первый признак подобия треугольников.
Ответ: Если два угла одного треугольника
равны двум углам другого треугольника, то такие треугольники подобны.
Слайд 6Упражнение 1
Подобны ли любые два: а) равносторонних треугольника; б) равнобедренных треугольника;
в) равнобедренных прямоугольных треугольника?
Ответ: а) Да;
б) нет;
в) да.
Слайд 7Упражнение 2
Стороны треугольника равны 5 см, 8 см и 10 см.
Найдите стороны подобного ему треугольника, если коэффициент подобия равен: а) 0,5; б) 2.
Ответ: а) 2,5 см, 4 см и 5 см;
б) 10 см, 16 см и 20 см.
Слайд 8Упражнение 3
Подобны ли прямоугольные треугольники, если у одного из них есть
угол 40о, а у другого 50о?
Ответ: Да.
Слайд 9Упражнение 4
Два треугольника подобны. Два угла одного треугольника равны 55о и
80о. Найдите наименьший угол второго треугольника.
Ответ: 45о.
Слайд 10Упражнение 5
В подобных треугольниках АВС и А1В1С1 АВ = 8 см,
ВС = 10 см, А1В1 = 5,6 см, А1С1 = 10,5 см. Найдите АС и В1С1.
Ответ: AC = 15 см, B1C1 = 7 см.
Слайд 12Упражнение 7
Стороны треугольника относятся как 5:3:7. Найдите стороны подобного ему треугольника,
у которого: а) периметр равен 45 см; б) меньшая сторона равна 5 см; в) большая сторона равна 7 см; г) разность большей и меньшей сторон составляет 2 см.
Ответ: а) 15 см, 9 см, 21 см;
в) 5 см, 3 см, 7 см;
г) 2,5 см, 1,5 см, 3,5 см.
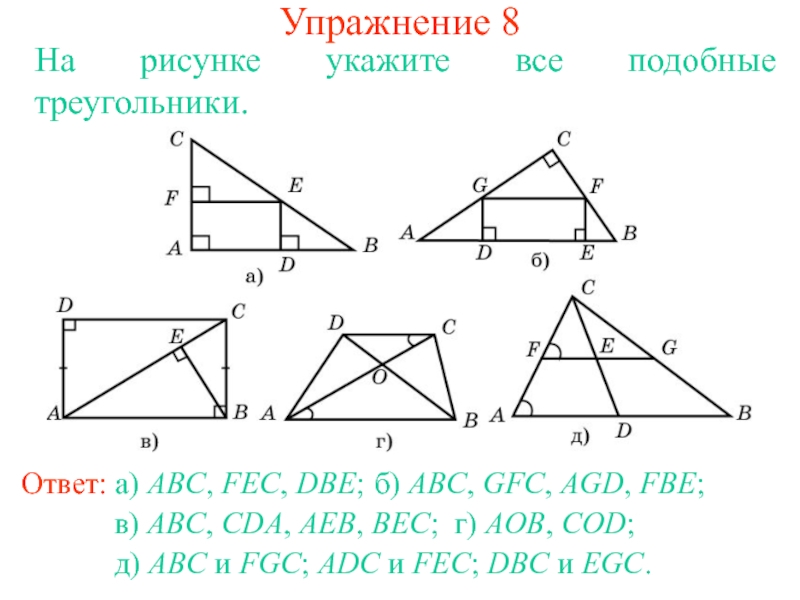
Слайд 13Упражнение 8
На рисунке укажите все подобные треугольники.
Ответ: а) ABC, FEC, DBE;
б) ABC, GFC, AGD, FBE;
в) ABC, CDA, AEB, BEC;
г) AOB, COD;
д) ABC и FGC; ADC и FEC; DBC и EGC.
Слайд 15Упражнение 10
У двух равнобедренных треугольников углы между боковыми сторонами равны. Боковая
сторона и основание одного треугольника равны соответственно 17 см и 10 см, основание другого равно 8 см. Найдите его боковую сторону.
Ответ: 13,6 см.
Слайд 16Упражнение 11
Катеты одного прямоугольного треугольника на 3 см больше катетов другого
прямоугольного треугольника. Подобны ли треугольники?
Ответ: Нет.
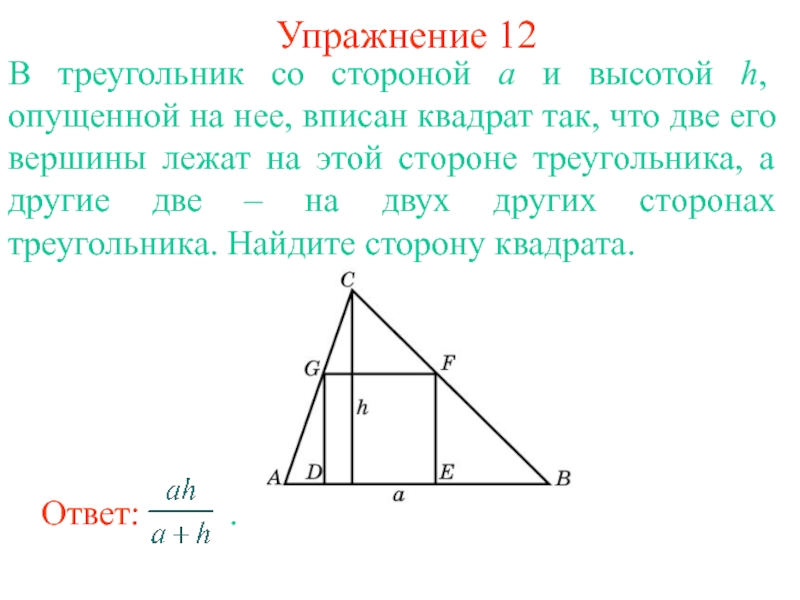
Слайд 17Упражнение 12
В треугольник со стороной а и высотой h, опущенной на
нее, вписан квадрат так, что две его вершины лежат на этой стороне треугольника, а другие две – на двух других сторонах треугольника. Найдите сторону квадрата.
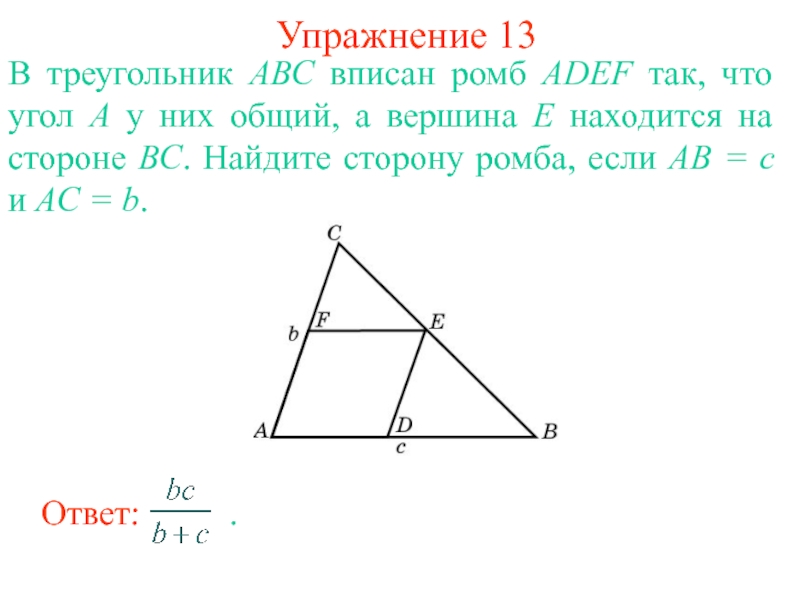
Слайд 18Упражнение 13
В треугольник АВС вписан ромб ADEF так, что угол А
у них общий, а вершина Е находится на стороне ВС. Найдите сторону ромба, если АВ = с и АС = b.
Слайд 19Упражнение 14
Можно ли треугольник пересечь прямой, непараллельной основанию, так, чтобы отсечь
от него подобный треугольник? В каком случае это невозможно?
Ответ: Можно, если треугольник неравносторонний.
Слайд 20Упражнение 15
Ответ: DEK и DLF, DEK и ELK, DLF и ELK,
DFK и DLE, DFK и FLK, DLE и FLK.
На рисунке DL – биссектриса треугольника DEF, вписанного в окружность. DL пересекает окружность в точке K, которая соединена отрезками с вершинами E и F треугольника. Найдите подобные треугольники.
Слайд 21Упражнение 16
Ответ: ABH и ADC, ACH и ADB, ABM и CDM,
BMD и AMC
В окружность вписан остроугольный треугольник ABC, AH – его высота, AD – диаметр окружности, который пересекает сторону BC в точке M. Точка D соединена с вершинами B и C треугольника. Найдите подобные треугольники.
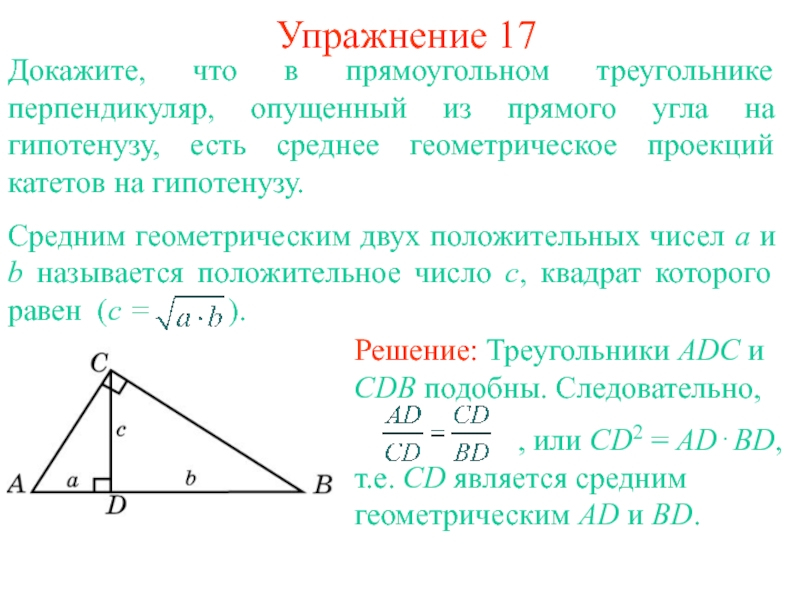
Слайд 22Упражнение 17
Докажите, что в прямоугольном треугольнике перпендикуляр, опущенный из прямого угла
на гипотенузу, есть среднее геометрическое проекций катетов на гипотенузу.
Средним геометрическим двух положительных чисел a и b называется положительное число c, квадрат которого равен (c = ).
Средним геометрическим двух положительных чисел a и b называется положительное число c, квадрат которого равен (c = ).
