- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии 7 класс на тему: Сумма углов треугольника
Содержание
- 1. Презентация по геометрии 7 класс на тему: Сумма углов треугольника
- 2. Три пути ведут к знанию: Путь
- 3. Цели урока: сформулировать и доказать
- 4. Повторение изученное …
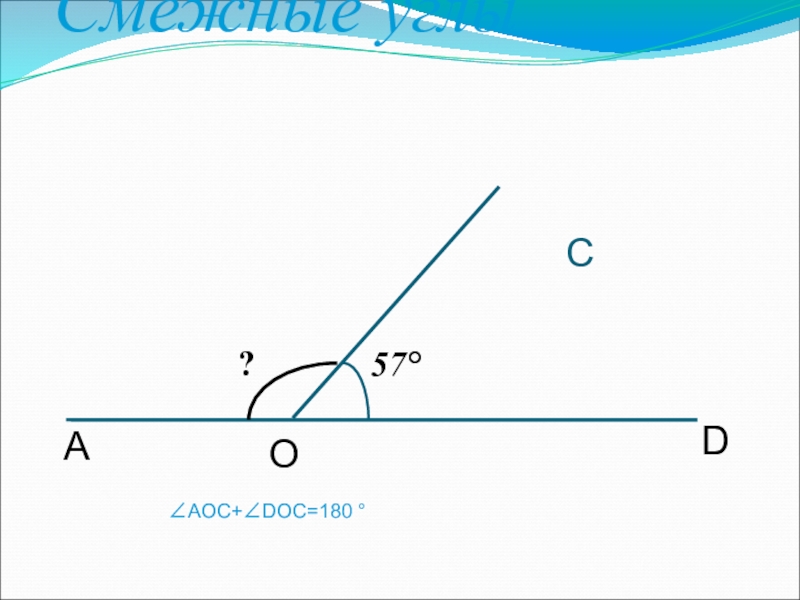
- 5. Смежные углы?57°АDОС∠АОС+∠DОС=180 °
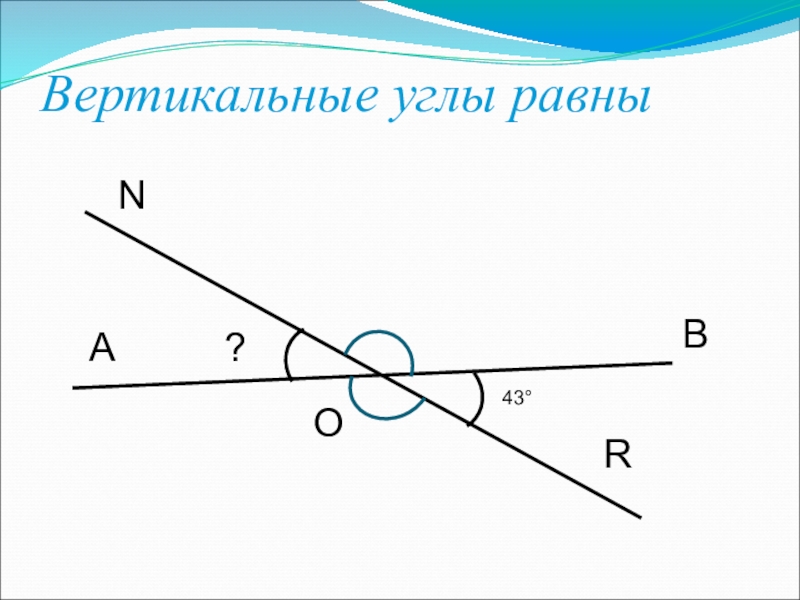
- 6. Вертикальные углы равныАОВRN?43°
- 7. Сумма односторонних углов равна 1800 4201380abaIIbc
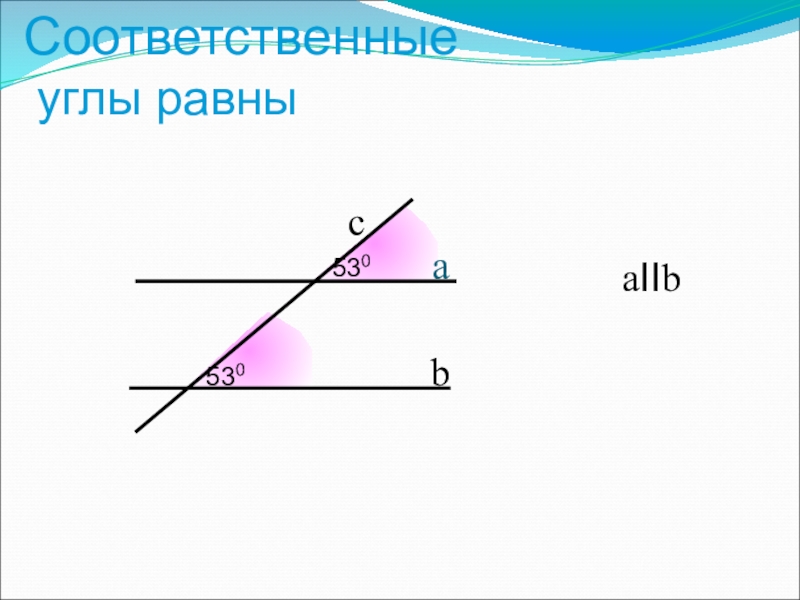
- 8. 530Соответственные углы равны530abaIIbc
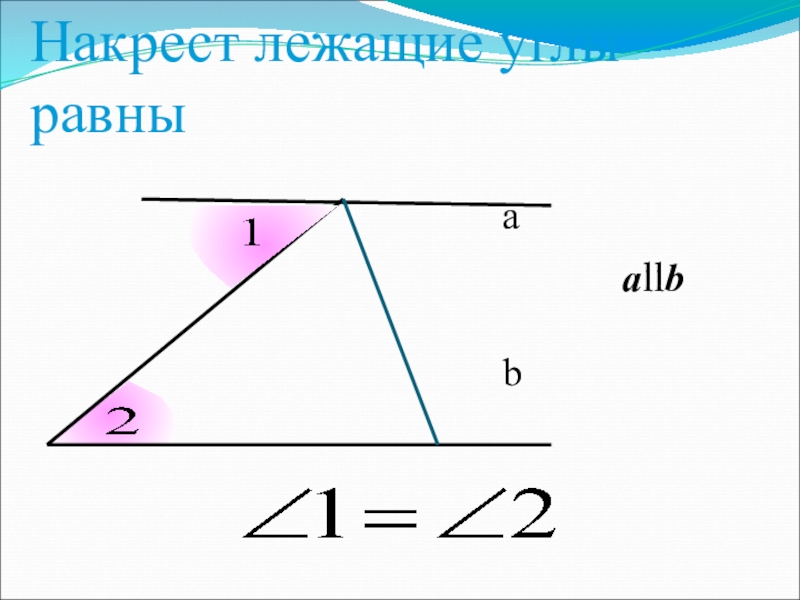
- 9. abНакрест лежащие углы равныallb
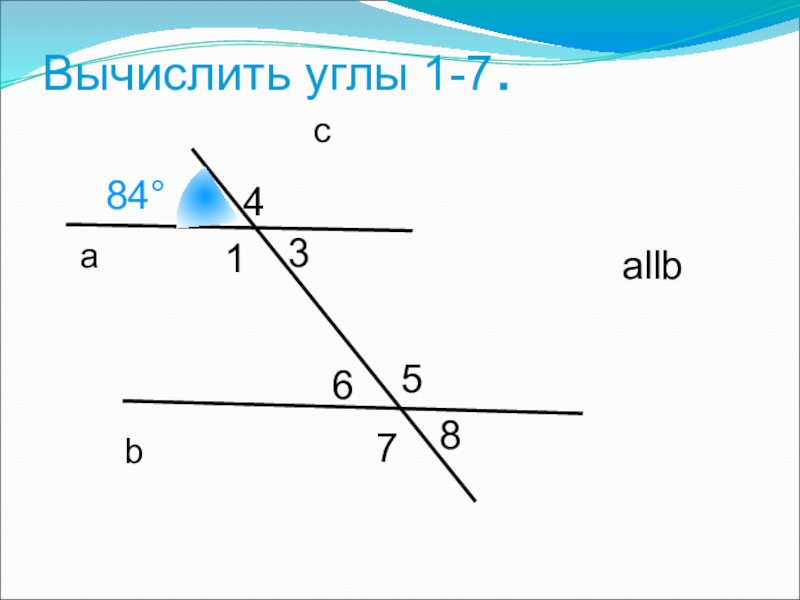
- 10. аbc1345678Вычислить углы 1-7. allb84°
- 11. Виды треугольников
- 12. Решение задачи по готовому чертежу.
- 13. Решите задачуДано: а||d∠1 = 72°∠3 = 32°Найдите: ∠ 2а12354cdb
- 14. Докажем теорему.
- 15. Теорема о сумме углов треугольникаТеорема: Сумма углов
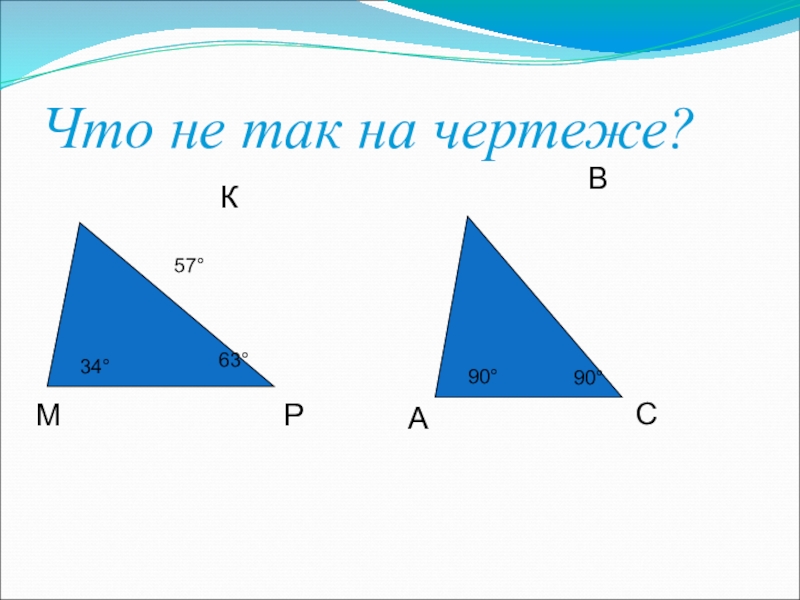
- 16. Что не так на чертеже?
- 17. Решение задач на применение теоремы.
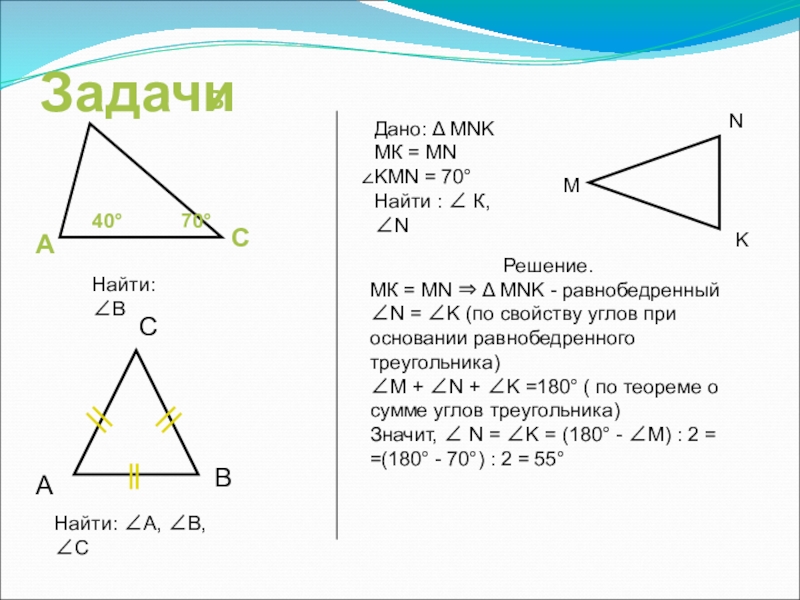
- 18. ЗадачиНайти: ∠ВНайти: ∠А, ∠В, ∠СДано: Δ MNKМК
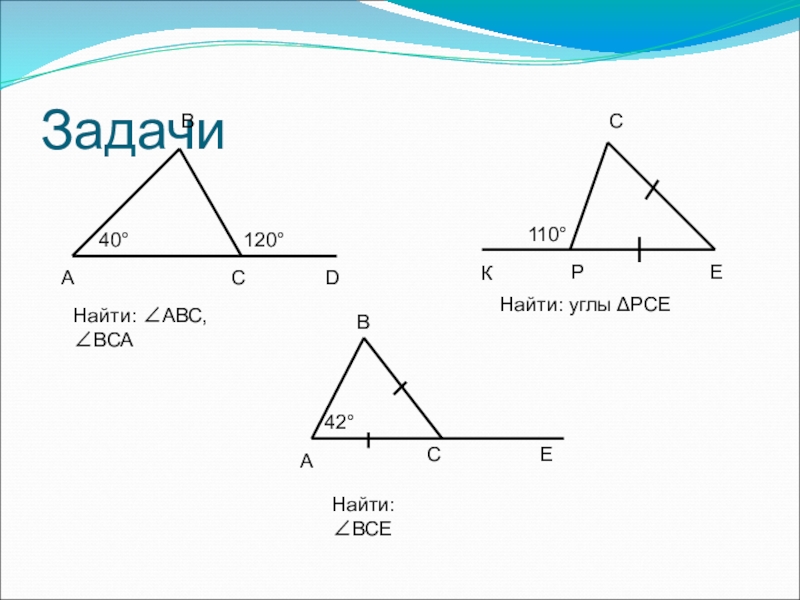
- 19. ЗадачиНайти: ∠АВС, ∠ВСАНайти: углы ΔРСЕНайти: ∠ВСЕ
- 20. Внешний угол треугольникаВнешний угол треугольника – это
- 21. Свойство внешнего угла треугольникаДано: ΔАВС∠ВСD – внешний
- 22. Задача Найти: углы ΔАВСРешите задачу, используя свойство
- 23. Домашнее заданиеП.п. 30,31№ 227(б, в)№ 228(а)
Три пути ведут к знанию: Путь размышления- это путь самый благородный, Путь подражания -это путь самый легкий и путь Опыта -это путь самый горький.
Слайд 2 Три пути ведут к знанию:
Путь размышления- это путь самый
благородный,
Путь подражания -это путь самый легкий и путь
Опыта -это путь самый горький.
Конфуций.
Путь подражания -это путь самый легкий и путь
Опыта -это путь самый горький.
Конфуций.
Слайд 3Цели урока:
сформулировать и доказать теорему о сумме
углов треугольника;
сформулировать и доказать теорему о внешнем угле треугольника;
рассмотреть задачи на применение доказанных теорем.
сформулировать и доказать теорему о внешнем угле треугольника;
рассмотреть задачи на применение доказанных теорем.
Слайд 15Теорема о сумме углов треугольника
Теорема:
Сумма углов треугольника равна 180°
Дано: Δ
АВС
Доказать: ∠А + ∠В + ∠С = 180°
Доказательство:
а⎥⎜АВ, С∈ а
∠ 1 =∠4
∠ 3 =∠5
∠4 + ∠2 + ∠5=180°
Значит, ∠1 + ∠2 + ∠3=180°
Доказать: ∠А + ∠В + ∠С = 180°
Доказательство:
а⎥⎜АВ, С∈ а
∠ 1 =∠4
∠ 3 =∠5
∠4 + ∠2 + ∠5=180°
Значит, ∠1 + ∠2 + ∠3=180°
а
1
2
3
5
4
Слайд 18Задачи
Найти: ∠В
Найти: ∠А, ∠В, ∠С
Дано: Δ MNK
МК = MN
KMN = 70°
Найти
: ∠ К, ∠N
Решение.
МК = MN ⇒ Δ MNK - равнобедренный
∠N = ∠K (по свойству углов при основании равнобедренного треугольника)
∠M + ∠N + ∠K =180° ( по теореме о сумме углов треугольника)
Значит, ∠ N = ∠K = (180° - ∠M) : 2 = =(180° - 70°) : 2 = 55°
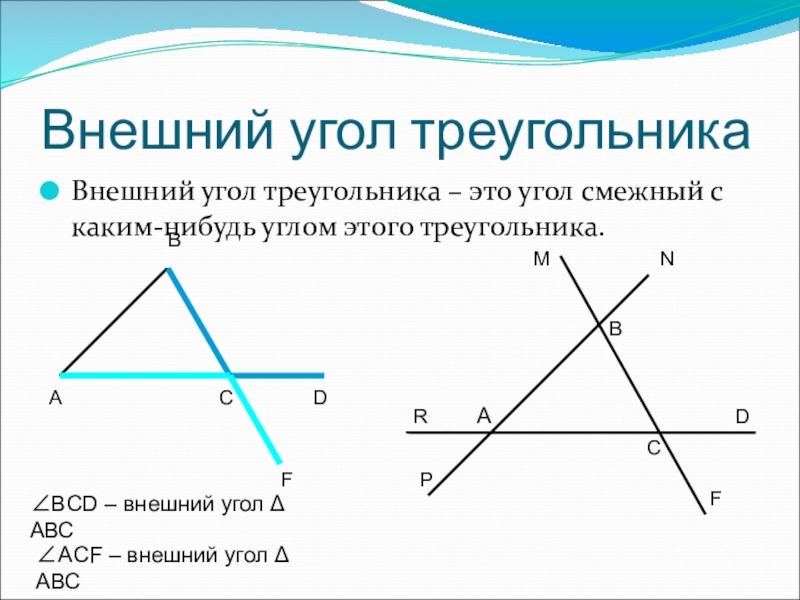
Слайд 20Внешний угол треугольника
Внешний угол треугольника – это угол смежный с каким-нибудь
углом этого треугольника.
∠BCD – внешний угол Δ АВС
F
∠АCF – внешний угол Δ АВС
Слайд 21Свойство внешнего угла треугольника
Дано: ΔАВС
∠ВСD – внешний угол ΔАВС
Доказать: ∠ВСD =
∠А + ∠В
Теорема
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
Доказательство:
∠АСВ + ∠ВСD = 180° (по свойству смежных углов)
∠АСВ + (∠А + ∠В) =180° (по теореме о сумме углов треугольника)
Значит, ∠ВСD = ∠А + ∠В
Слайд 22Задача
Найти: углы ΔАВС
Решите задачу, используя свойство внешнего угла треугольника
∠ВСЕ = ∠А
+ ∠В (по свойству внешнего угла треугольника)
ВС=АС ⇒ ΔАВС - равнобедренный
Значит,
∠А = ∠С = ∠ВСЕ : 2 = 130°: 2 = 65°
∠ВСА =180° - ∠ВСЕ
∠ВСА =180° - 130°=50°
ВС=АС ⇒ ΔАВС - равнобедренный
Значит,
∠А = ∠С = ∠ВСЕ : 2 = 130°: 2 = 65°
∠ВСА =180° - ∠ВСЕ
∠ВСА =180° - 130°=50°
