- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии 10 класс
Содержание
- 1. Презентация по геометрии 10 класс
- 2. Урок № 11Параллельность прямой и плоскостиГеометрия – 109.10.17Малюгин Николай ИвановичУчитель математикиБоровская СОШ Тюменского района Тюменской области
- 3. Признак параллельности прямой и плоскости.Если прямая, не
- 4. Утверждение 1:Если плоскость проходит через данную прямую,
- 5. Утверждение 2:Если одна из двух параллельных прямых
- 6. АВМСD1). A (ABM),
- 7. βcp β = p p
- 8. АВСDE12?b
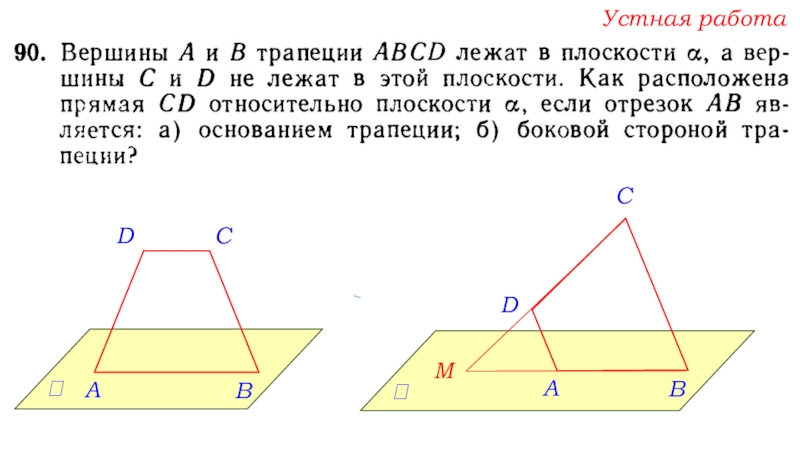
- 9. Устная работаАВСDАВСDМ
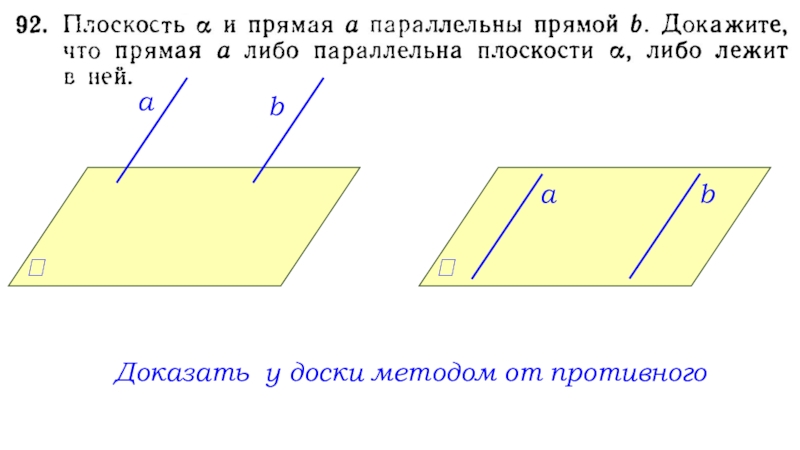
- 10. βаcbMДано: а ∥ b, a ,
- 11. аbаbДоказать у доски методом от противного
Урок № 11Параллельность прямой и плоскостиГеометрия – 109.10.17Малюгин Николай ИвановичУчитель математикиБоровская СОШ Тюменского района Тюменской области
Слайд 2Урок
№ 11
Параллельность прямой и плоскости
Геометрия – 10
9.10.17
Малюгин Николай Иванович
Учитель математики
Боровская
СОШ Тюменского района Тюменской области
Слайд 3Признак параллельности прямой и плоскости.
Если прямая, не лежащая в данной плоскости,
параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
а
b
Дано:
а ∥ b
а
b
Доказать:
а ∥
Доказательство:
Провести самостоятельно методом от противного
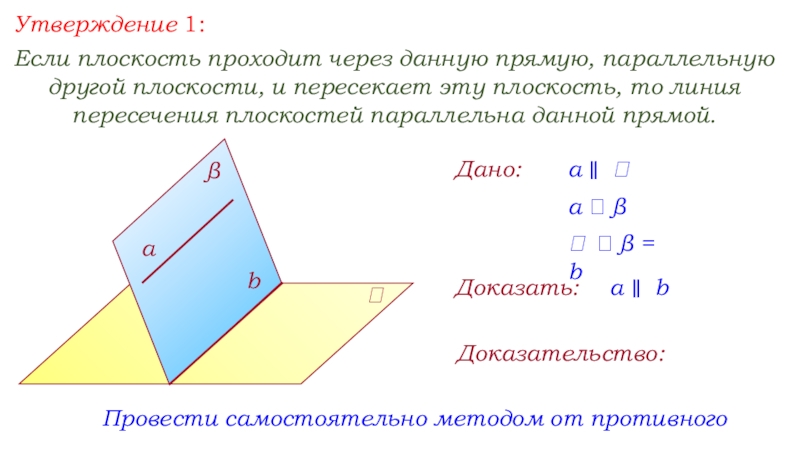
Слайд 4Утверждение 1:
Если плоскость проходит через данную прямую, параллельную другой плоскости, и
пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
β
а
b
Дано:
а ∥
а β
β = b
Доказать:
а ∥ b
Доказательство:
Провести самостоятельно методом от противного
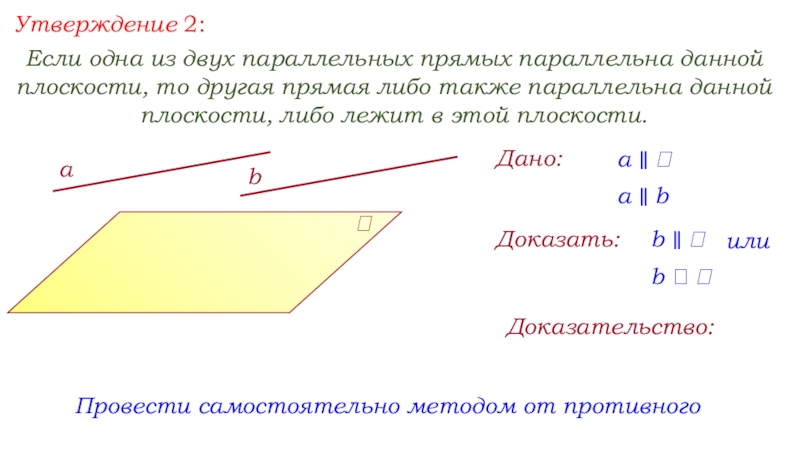
Слайд 5Утверждение 2:
Если одна из двух параллельных прямых параллельна данной плоскости, то
другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
а
b
Дано:
а ∥
а ∥ b
Доказать:
b ∥
Доказательство:
Провести самостоятельно методом от противного
b
или