- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к внеклассному мероприятию по теме:Многогранники
Содержание
- 1. Презентация к внеклассному мероприятию по теме:Многогранники
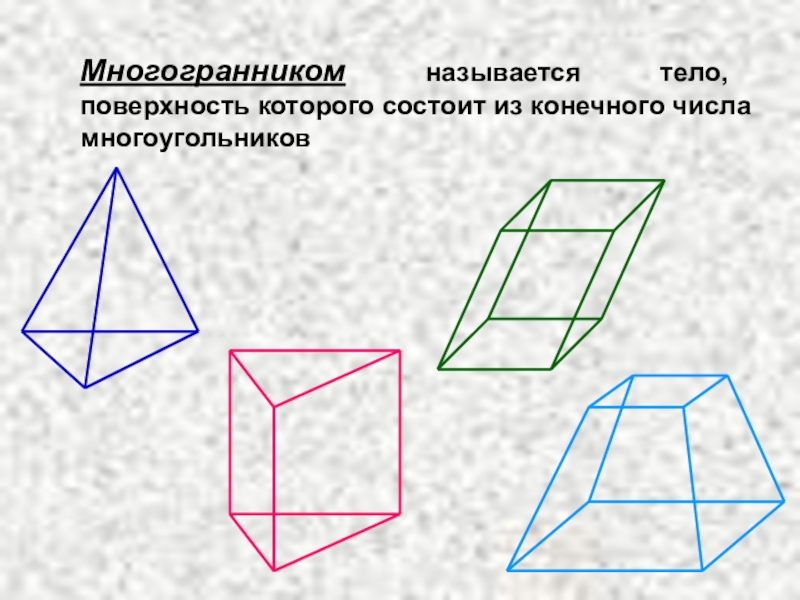
- 2. Многогранником называется тело, поверхность которого состоит из конечного числа многоугольников
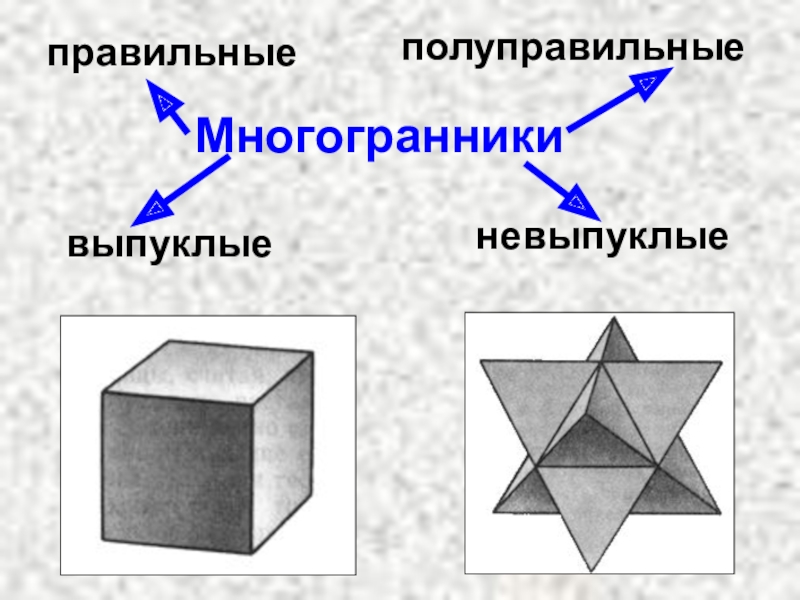
- 3. Многогранникивыпуклыеневыпуклыеправильныеполуправильные
- 4. Правильные многогранникиНазвания правильных многогранников пришли из Греции.
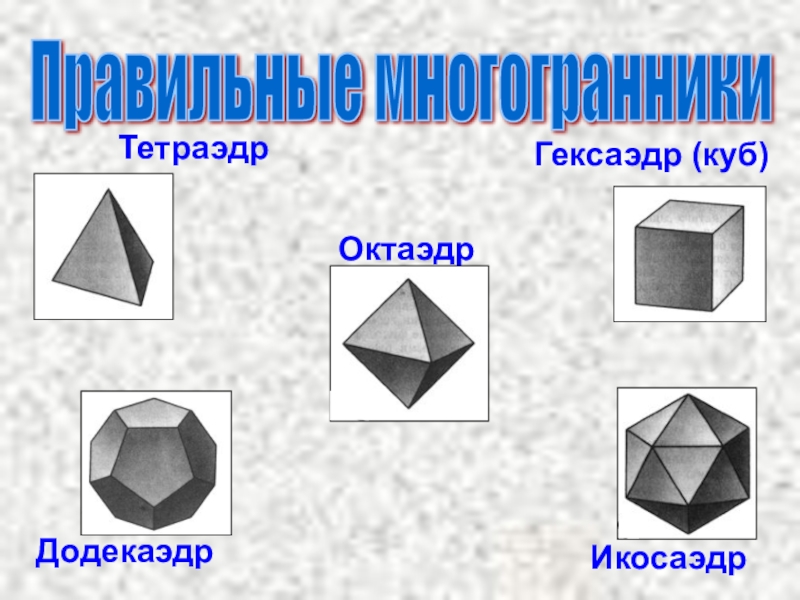
- 5. ТетраэдрГексаэдр (куб)ОктаэдрДодекаэдрИкосаэдрПравильные многогранники
- 6. Простейшим среди правильных многогранников является тетраэдр. Его
- 7. ГексаэдрКуб составлен из шести квадратов. Каждая его
- 8. Октаэдр Октаэдр составлен из восьми равносторонних треугольников. Каждая
- 9. Додекаэдр Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая
- 10. Икосаэдр Икосаэдр составлен из двадцати равносторонних треугольников.Каждая его
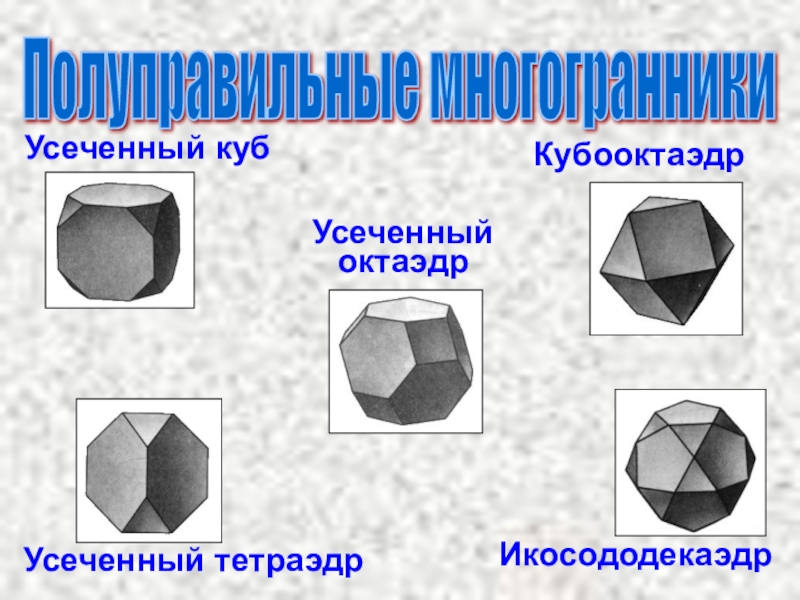
- 11. Усеченный кубКубооктаэдрУсеченныйоктаэдрУсеченный тетраэдрИкосододекаэдрПолуправильные многогранники
- 12. Малый звездчатыйдодекаэдрЗвездчатыйоктаэдрБольшой додекаэдрБольшойзвездчатый додекаэдрТела Кеплера-Пуансо
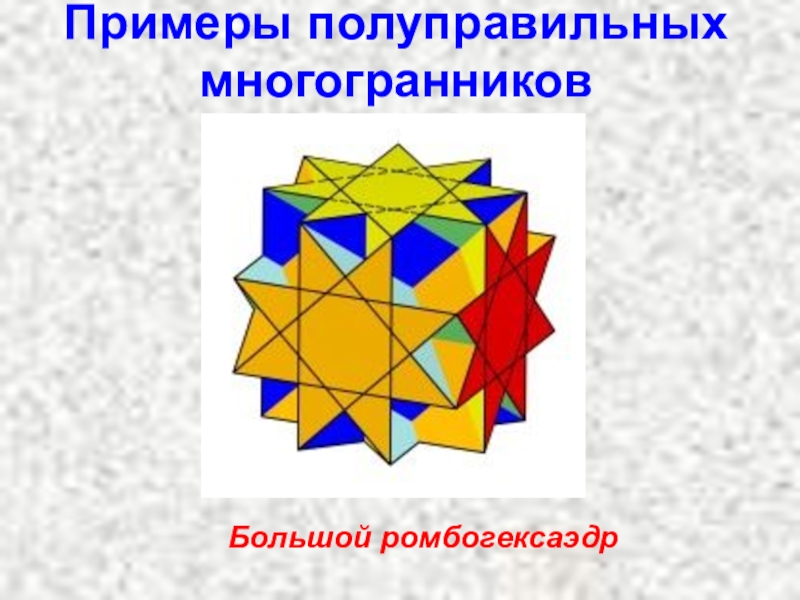
- 13. Примеры полуправильных многогранниковБольшой ромбогексаэдр
- 14. Примеры полуправильных многогранниковБольшой курносый икосододекаэдр
- 15. Примеры полуправильных многогранниковКвазиромбокубоктаэдр
- 16. Многогранники в архитектуре
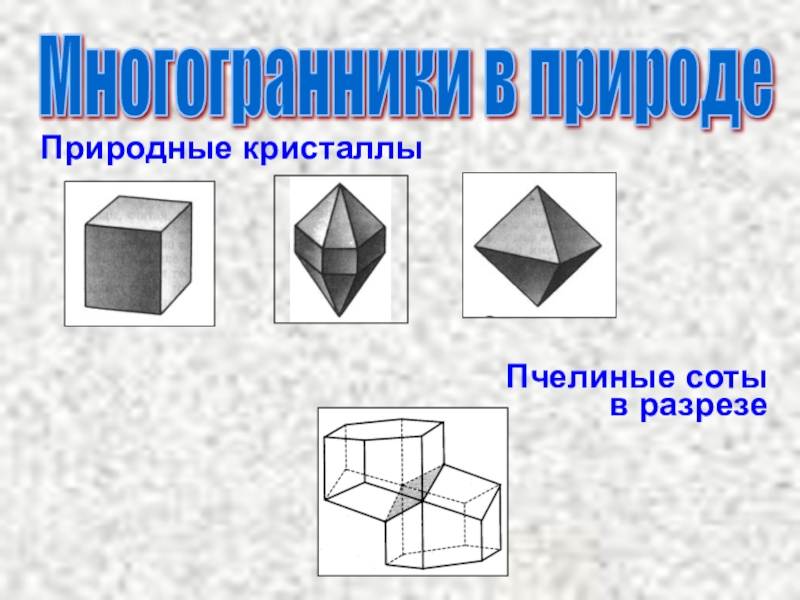
- 17. Природные кристаллыПчелиные сотыв разрезеМногогранники в природе
- 18. Многогранники в искусстве Сальвадор Дали. Тайная вечеря (1955)
- 19. Морис Эшер. “Рептилии”(литография, 1943 г).
- 20. Надгробный памятник в кафедральном соборе Солсбери
- 21. Титульный лист книги Ж. Кузена «Книга о перспективе»
Многогранником называется тело, поверхность которого состоит из конечного числа многоугольников
Слайд 2Многогранником называется тело, поверхность которого состоит из конечного числа многоугольников
Слайд 4Правильные многогранники
Названия правильных многогранников пришли из Греции. В дословном переводе с
греческого "тетраэдр", "октаэдр", "гексаэдр", "додекаэдр", "икосаэдр" означают: "четырехгранник", "восьмигранник", "шестигранник". "двенадцатигранник", "двадцатигранник". Этим красивым телам посвящена 13-я книга "Начал" Евклида. Их еще называют телами Платона, т.к. они занимали важное место в философской концепции Платона об устройстве мироздания.
Слайд 6 Простейшим среди правильных многогранников является тетраэдр.
Его четыре грани – равносторонние
треугольники. Каждая его вершина является вершиной трех треугольников.
Таким образом, тетраэдр имеет 4 грани, 4 вершины и 6 ребер.
Таким образом, тетраэдр имеет 4 грани, 4 вершины и 6 ребер.
Тетраэдр
Слайд 7Гексаэдр
Куб составлен из шести квадратов. Каждая его вершина является вершиной трех
квадратов. Таким образом, куб имеет 6 граней, 8 вершин и 12 ребер.
Слайд 8Октаэдр
Октаэдр составлен из восьми равносторонних треугольников. Каждая его вершина является вершиной
четырех треугольников. Противоположные грани лежат в параллельных плоскостях.
Таким образом, октаэдр имеет 8 граней, 6 вершин и 12 ребер.
Таким образом, октаэдр имеет 8 граней, 6 вершин и 12 ребер.
Слайд 9Додекаэдр
Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая его вершина является вершиной
трех пятиугольников.
Таким образом, додекаэдр имеет 12 граней, 20 вершин и 30 ребер.
Таким образом, додекаэдр имеет 12 граней, 20 вершин и 30 ребер.
Слайд 10Икосаэдр
Икосаэдр составлен из двадцати равносторонних треугольников.
Каждая его вершина является вершиной пяти
треугольников.
Таким образом икосаэдр имеет 20 граней, 12 вершин и 30 ребер.
Таким образом икосаэдр имеет 20 граней, 12 вершин и 30 ребер.
Слайд 11Усеченный куб
Кубооктаэдр
Усеченный
октаэдр
Усеченный тетраэдр
Икосододекаэдр
Полуправильные многогранники
Слайд 12Малый звездчатый
додекаэдр
Звездчатый
октаэдр
Большой додекаэдр
Большой
звездчатый додекаэдр
Тела Кеплера-Пуансо
