- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к устной работе на уроке геометрии в 10 классе по теме
Содержание
- 1. Презентация к устной работе на уроке геометрии в 10 классе по теме
- 2. Дано:Доказать: АС⊥(АМВ)Доказательство:АС⊥АВ, АС⊥АМ (по условию), АС
- 3. Задача 2. Какой плоскости грани тетраэдра DАВС
- 4. BMDC-прямоугольник. Доказать: прямая CD перпендикулярна плоскости АВС.Дано:
- 5. ABCD-прямоугольник. Доказать: AD⊥АМ. М
Слайд 2Дано:
Доказать: АС⊥(АМВ)
Доказательство:
АС⊥АВ, АС⊥АМ (по условию),
АС (АМВ), АВ (АМВ),
АМ
⇒АС⊥ (АМВ) (по признаку перпендикулярности прямой и плоскости)
Задача 1.
Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости
М
А
В
С
Признак перпендикулярности прямой и плоскости
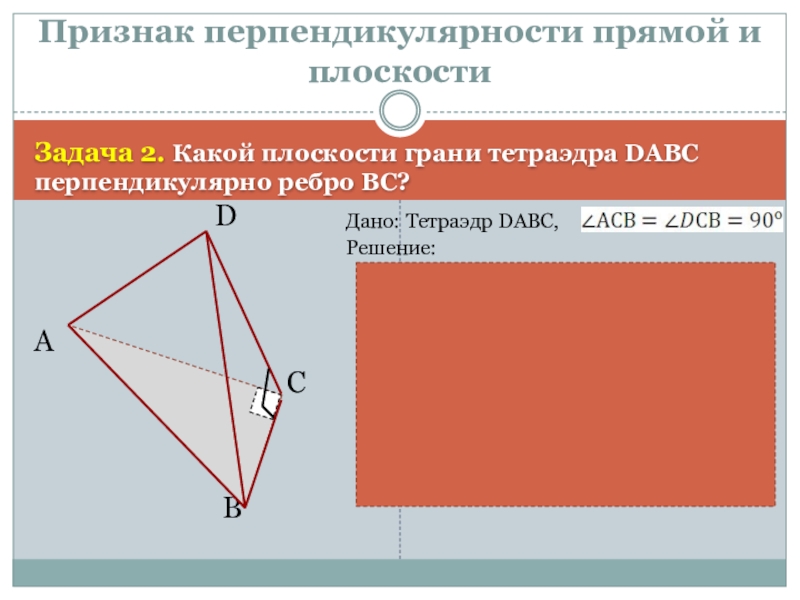
Слайд 3Задача 2. Какой плоскости грани тетраэдра DАВС перпендикулярно ребро ВС?
A
C
B
Дано: Тетраэдр DАВС,
Решение:
Так как , то
ВС⊥АС, ВС⊥DC.
Так как АС , DC ⊂ (ADC),
АС∩DC=С, то ВС⊥ (ADC) (по признаку перпендикулярности прямой и плоскости)
Ответ: ребро ВС перпендикулярно
грани (ADC) тетраэдра DАВС
Признак перпендикулярности прямой и плоскости
Слайд 4BMDC-прямоугольник. Доказать: прямая CD перпендикулярна плоскости АВС.
Дано: BMDC-прямоугольник.
Доказать:
Доказательство:
Т.к.
B С , СD⊥ ВC, CD⊥AВ ⇒
(по признаку
перпендикулярности
прямой и плоскости)
М D
В
C
А
Задача 3.
СD⊥ (АВC)
СD⊥ (АВC)
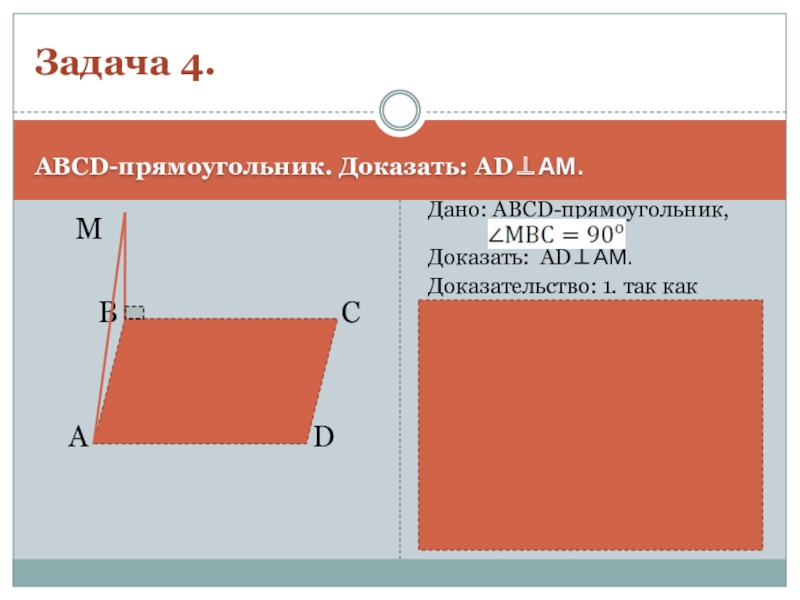
Слайд 5ABCD-прямоугольник. Доказать: AD⊥АМ.
М
В
А D
Дано: ABCD-прямоугольник,
Доказать: AD⊥АМ.
Доказательство: 1. так как ABCD-прямоугольник, то AD⊥АВ. Так как и AD‖ВС ⇒ AD⊥ВМ. 2. АВ⊂(АВМ), МВ⊂(АВМ), АВ∩ВМ=В ⇒ AD⊥(АМВ) (по признаку перпендикулярности прямой и плоскости). 3. Так как AD⊥(АМВ) и АМ ⊂(АВМ) ⇒ AD⊥АМ ( по определению).
Задача 4.