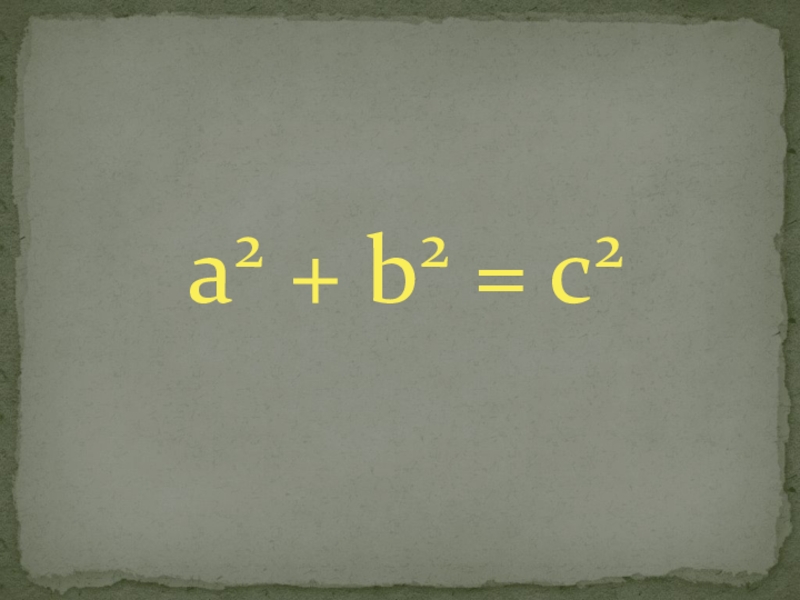- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Теорема Пифагора
Содержание
- 1. Презентация к уроку Теорема Пифагора
- 2. Историческая справка
- 3. Теорема формулируется так: площадь квадрата , построенного
- 4. « В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов». Современная формулировка
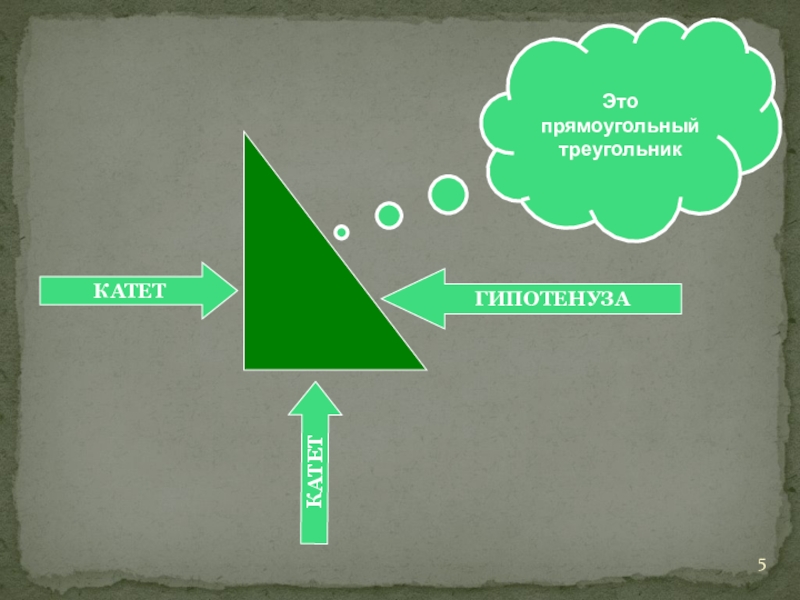
- 5. ГИПОТЕНУЗАКАТЕТКАТЕТЭто прямоугольный треугольник
- 6. a2 + b2 = c2
- 7. Обычно открытие этого утверждения приписывают древнегреческому философу
- 8. Вероятно , факт ,изложенный в теореме Пифагора
- 9. Для доказательства общего случая в Древней Индии
- 10. Квадрат, построенный на гипотенузе
- 11. Задача землемеров Землемеры Древнего Египта для построенияпрямого угла
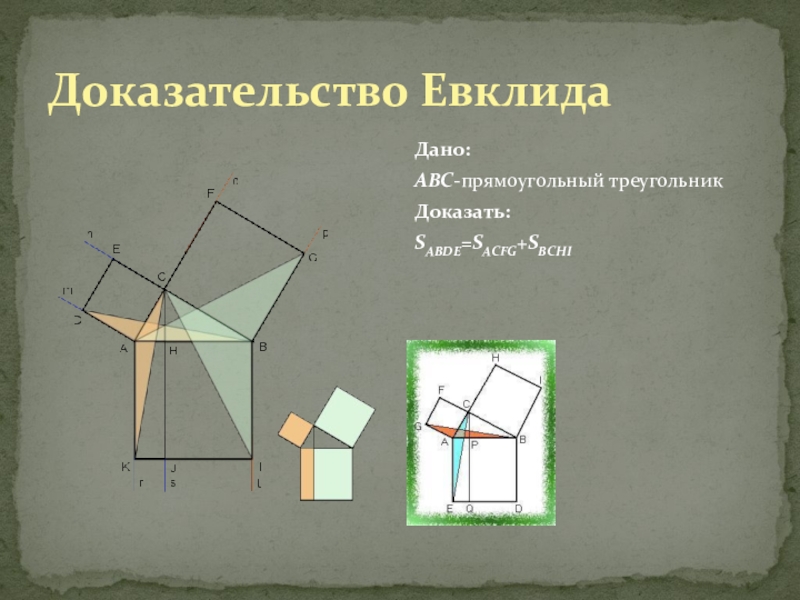
- 12. Доказательство Евклида Дано: ABC-прямоугольный треугольник Доказать:SABDE=SACFG+SBCHI
- 13. Пусть ABDE-квадрат, построенный на гипотенузе прямоугольного треугольника
- 14. Очевидно, что углы CAE=GAB(=A+90°); отсюда следует, что
- 15. Отсюда и из равенства треугольников ACE и
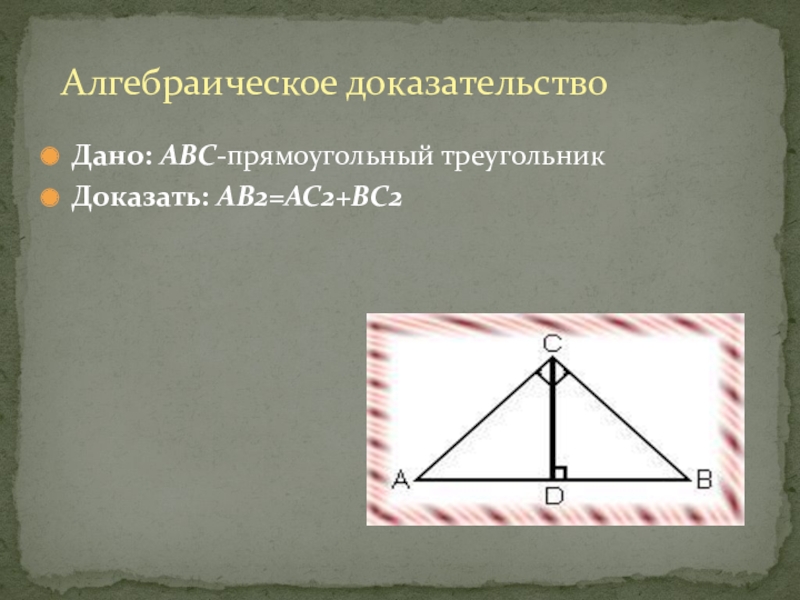
- 16. Дано: ABC-прямоугольный треугольникДоказать: AB2=AC2+BC2Алгебраическое доказательство
- 17. 1) Проведем высоту CD из вершины прямого угла
- 18. Геометрическое доказательствоДано: ABC-прямоугольный треугольникДоказать: BC2=AB2+AC2Доказательство: 1) Построим отрезок
- 19. SABED=2*AB*AC/2+BC2/23) Фигура ABED является трапецией, значит, её площадь
- 20. Доказательство Леонардо да Винчи Главные элементы доказательства — симметрия и движение.
- 21. Рассмотрим чертёж, как видно из симметрии, отрезок CI рассекает
- 22. Значение теоремы ПифагораИз теоремы Пифагора или с
- 23. Глубокое уважение к личности
- 24. Если отбросить сказки и
- 25. Пифагор- это не только великий
- 26. Мысль — превыше всего между людьми на
- 27. Открытие теоремы Пифагором
- 28. О теореме Пифагора.Пребудет вечной истина, как скоро
- 29. О теореме Пифагора Уделом истины не может быть
- 30. Родителями Пифагора были Мнесарх и Партенида с
- 31. Пифагор в 18-летнем возрасте покинул родной остров
- 32. Пифагор покинул Самос из-за несогласия с тиранической
- 33. Разногласия с тираном Поликратом вряд ли могли
- 34. У Пифагора была жена по имени Феано,
- 35. Спасибо за внимание! Конец презентации.
Слайд 2Историческая справка
(около 569г.- около 475г. до н.э.)
Основал пифагорейскую
школу, в которой рассматрива-
лись четыре науки: арифметика,
музыка(гармония), геометрия и
астрономия с астрологией.
Считал, что в основе всего
лежат числа и гармония.
«Все есть число».
Слайд 3Теорема формулируется так: площадь квадрата , построенного на гипотенузе прямоугольного треугольника
Формулировка теоремы
Слайд 4« В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
Современная формулировка
Слайд 7Обычно открытие этого утверждения приписывают древнегреческому философу и математику Пифагору (VI
Слайд 8Вероятно , факт ,изложенный в теореме Пифагора , был сначала установлен
Достаточно взглянуть на мозаику из черных и светлых треугольников, изображенную на рис. 1 , чтобы убедиться в справедливости теоремы для треугольника АВС : квадрат , построенный на гипотенузе , содержит 4 треугольника , а на каждом катете построен квадрат ,содержащий 2 треугольника.
Рис. 1
Слайд 9Для доказательства общего случая в Древней Индии располагали двумя способами: в
Доказательство
Рис. 2 а
Рис. 2 б
Слайд 10 Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на
Почтовая марка по случаю переименования острова Самос в остров Пифагорейон. На марке надпись: « т.Пифагора. Эллас. 350 драхи».
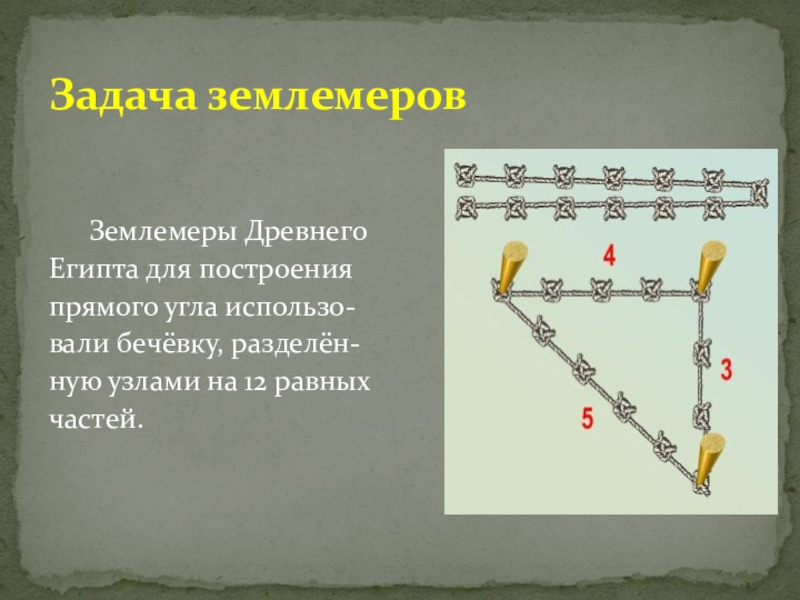
Слайд 11Задача землемеров
Землемеры Древнего
Египта для построения
прямого угла использо-
вали бечёвку, разделён-
ную узлами
частей.
Слайд 13Пусть ABDE-квадрат, построенный на гипотенузе прямоугольного треугольника ABC, а ACFG и
Доказательство:
Слайд 14Очевидно, что углы CAE=GAB(=A+90°); отсюда следует, что треугольники ACE и AGB(закрашенные
SPQEA=2SACE
Точно так же квадрат FCAG и треугольник BAG имеют общее основание GA и высоту AC; значит, SFCAG=2SGAB
Слайд 15Отсюда и из равенства треугольников ACE и GBA вытекает равновеликость прямоугольника
Слайд 171) Проведем высоту CD из вершины прямого угла С.
2) По определению косинуса угла
AB*AD=AC2.
3) Аналогично соsВ=BD/BC=BC/AB, значит
AB*BD=BC2.
4) Сложив полученные равенства почленно, получим:
AC2+BC2=АВ*(AD + DB)
AB2=AC2+BC2. Что и требовалось доказать.
Доказательство:
Слайд 18Геометрическое доказательство
Дано: ABC-прямоугольный треугольник
Доказать: BC2=AB2+AC2
Доказательство:
1) Построим отрезок CD равный отрезку AB на
Слайд 19SABED=2*AB*AC/2+BC2/2
3) Фигура ABED является трапецией, значит, её площадь равна:
SABED= (DE+AB)*AD/2.
4) Если приравнять
AB*AC+BC2/2=(DE+AB)(CD+AC)/2
AB*AC+BC2/2= (AC+AB)2/2
AB*AC+BC2/2= AC2/2+AB2/2+AB*AC
BC2=AB2+AC2.
Это доказательство было опубликовано в 1882 году Гэрфилдом.
Слайд 21Рассмотрим чертёж, как видно из симметрии, отрезок CI рассекает квадрат ABHJ на две одинаковые части
Пользуясь поворотом на 90 градусов против часовой стрелки вокруг точки A, мы усматриваем равенство заштрихованных фигур CAJI и DABG.
Теперь ясно, что площадь заштрихованной нами фигуры равна сумме половин площадей маленьких квадратов (построенных на катетах) и площади исходного треугольника. С другой стороны, она равна половине площади большого квадрата (построенного на гипотенузе) плюс площадь исходного треугольника. Таким образом, половина суммы площадей маленьких квадратов равна половине площади большого квадрата, а следовательно сумма площадей квадратов, построенных на катетах равна площади квадрата, построенного на гипотенузе.
Слайд 22Значение теоремы Пифагора
Из теоремы Пифагора или с её помощью можно вы-
вести
ем, связывавшим длины сторон треугольников. Потом узнали, как находить
длины сторон и углы остроугольных и тупоугольных треугольников. Возникла целая наука тригонометрия. Сейчас тригонометрию применяют
Даже для измерения расстояний между космическими кораблями.
Слайд 23 Глубокое уважение к личности Пифагора сопровождалось множеством легенд,
Легенда о Пифагоре
Слайд 24 Если отбросить сказки и выдумки, то окажется, что
Слайд 25 Пифагор- это не только великий математик, но и великий
Пифагор. Гравюра из старинной книги.
Слайд 26Мысль — превыше всего между людьми на земле.
Не садись на
По торной дороге не ходи (т. е. следуй не мнениям толпы, а мнениям немногих понимающих).
Ласточек в доме не держи (т. е. не принимай гостей болтливых и не сдержанных на язык).
Будь с тем, кто ношу взваливает, не будь с тем, кто ношу сваливает (т. е. поощряй людей не к праздности, а к добродетели, к труду).
В перстне изображений не носи (т. е. не выставляй напоказ перед людьми, как ты судишь и думаешь о богах).
Слайд 27
Открытие теоремы Пифагором окружено ореолом красивых легенд.
Легенды об открытии
теоремы Пифагора
Слайд 28О теореме Пифагора.
Пребудет вечной истина, как скоро
Её познает
И ныне теорема Пифагора верна,
Как и в его далёкий век.
А.Шамиссо
Слайд 29О теореме Пифагора
Уделом истины не может быть забвенье,
Как только мир её
И теорема та, что дал нам Пифагор,
Верна теперь, как в день её рожденья.
За светлый луч с небес вознес благодаренье
Мудрец богам не так, как было до тех пор.
Ведь целых сто быков послал он под топор,
Чтоб их сожгли как жертвоприношенье.
Быки с тех пор, как только весть услышат,
Что новой истины уже следы видны,
Отчаянно мычат и ужаса полны:
Им Пифагор навек внушил тревогу.
Не в силах преградить той истине дорогу,
Они, закрыв глаза, дрожат и еле дышат.
Суть истины вся в том, что нам она-навечно,
Когда хоть раз в прозрений её увидим свет,
И теорема Пифагора через столько лет
Для нас, как для него, бесспорна, безупречна.
На радостях богам был Пифагором дан обет:
За то, что мудрости коснулся бесконечной,
Он сто быков заклал, благодаря предвечных;
Моленья и хвалы вознес он жертве вслед.
С тех пор быки, когда, учуют, тужась,
Что к новой истине людей опять подводит след,
Ревут остервенело, так что слушать мочи нет,
Такой в них Пифагор вселил навеки ужас,
Быкам, бессильным новой правде противостоять,
Что остается? - Лишь, глаза закрыв, реветь, дрожать.
Слайд 30Родителями Пифагора были Мнесарх и Партенида с Самоса.
Рождение ребёнка будто
По словам античных авторов, Пифагор встретился чуть ли не со всеми известными мудрецами той эпохи, греками, персами, халдеями, египтянами, впитал в себя всё накопленное человечеством знание.
В юном возрасте Пифагор отправился в Египет, чтобы набраться мудрости и тайных знаний у египетских жрецов. Диоген и Порфирий пишут, что самосский тиран Поликрат снабдил Пифагора рекомендательным письмом к фараону Амасису, благодаря чему он был допущен к обучению и посвящён в таинства, запретные для прочих чужеземцев.
Биография Пифагора
Слайд 31Пифагор в 18-летнем возрасте покинул родной остров и, объехав мудрецов в
Слайд 32Пифагор покинул Самос из-за несогласия с тиранической властью Поликрата в 40-летнем
Слайд 33Разногласия с тираном Поликратом вряд ли могли послужить причиной отъезда Пифагора,
Пифагор поселился в греческой колонии Кротоне в Южной Италии, где нашёл много последователей. Их привлекала не только мистическая философия, которую он убедительно излагал, но и предписываемый им образ жизни с элементами здорового аскетизма и строгой морали. Пифагор проповедовал нравственное облагораживание невежественного народа, достигнуть которого возможно там, где власть принадлежит касте мудрых и знающих людей, и которым народ повинуется в чём-то безоговорочно, как дети родителям, а в остальном сознательно, подчиняясь нравственному авторитету. Ученики Пифагора образовали своего рода религиозный орден, или братство посвящённых, состоящий из касты отобранных единомышленников, буквально обожествляющих своего учителя и основателя. Этот орден фактически пришёл в Кротоне к власти, однако из-за антипифагорейских настроений в конце VI в. до н. э. Пифагору пришлось удалиться в другую греческую колонию Метапонт, где он и умер. Почти 450 лет спустя во времена Цицерона (I в. до н. э.) в Метапонте как одну из достопримечательностей показывали склеп Пифагора
Слайд 34У Пифагора была жена по имени Феано, сын Телавг и дочь
Пифагор возглавлял своё тайное общество тридцать девять лет, тогда приблизительная дата смерти Пифагора может быть отнесена к 491 до н. э., к началу эпохи греко-персидских войн. Пифагор мирно скончался в возрасте 80 лет, или же в 90 лет (по неназванным другим источникам). Из этого следует дата смерти 490 до н. э. (или 480 до н. э., что маловероятно). Евсевий Кесарийский в своей хронографии обозначил 497 до н. э. как год смерти Пифагора.