стороны одного треугольника пропорциональны сходственным сторонам другого.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Признаки подобия. Геометрия. 8 класс. Атанасян
Содержание
- 1. Презентация к уроку Признаки подобия. Геометрия. 8 класс. Атанасян
- 2. Первый признак подобия треугольниковЕСЛИ ДВА УГЛА ОДНОГО
- 3. ЗАДАЧА №551Дано: ABCD – параллелограмм,Е принадлежит DC;F=AE
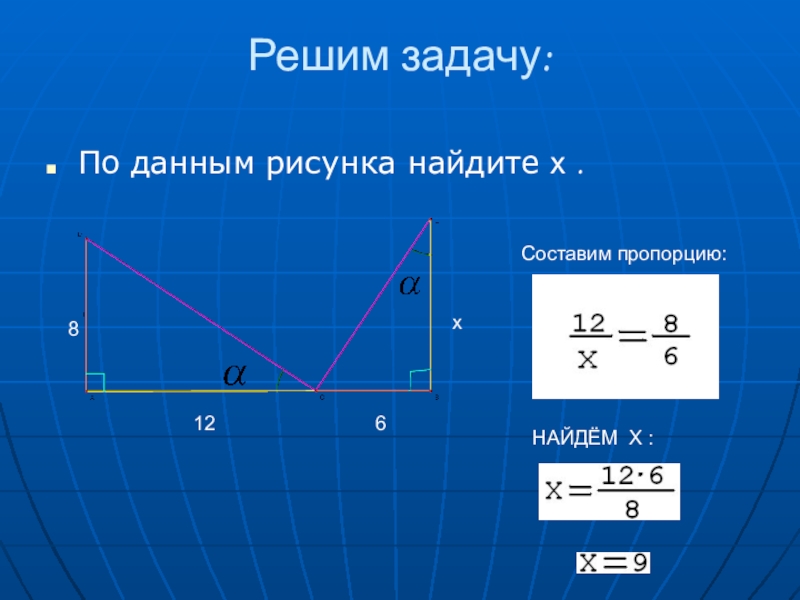
- 4. Решим задачу:По данным рисунка найдите х .
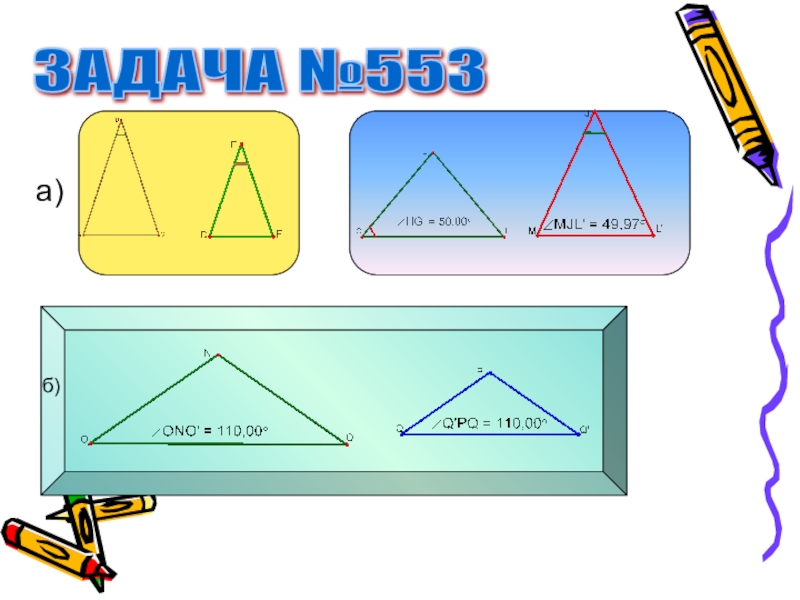
- 5. ЗАДАЧА №553а)б)
- 6. Второй признак подобия треугольников: Если две
- 7. Задача №559На одной из сторон данного угла
- 8. Третий признак подобияЕсли три
- 9. Треугольники подобны, если Подобны ли треугольники ABC
- 10. Средняя линия треугольникаСредней линией треугольника называется отрезок,
- 11. ЗадачаДоказать, что медианы треугольника пересекаются в одной
- 12. ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В
- 13. 1. Высота прямоугольного треугольника, проведённая из вершины
- 14. Катет прямоугольного треугольника есть среднее пропорциональное между
- 15. Самостоятельная работаВариант 1Дано: Вариант 2Дано:Найти:Найти:
- 16. Слайд 16
Первый признак подобия треугольниковЕСЛИ ДВА УГЛА ОДНОГО ТРЕУГОЛЬНИКА СООТВЕТСТВЕННО РАВНЫ ДВУМ УГЛАМ ДРУГОГО, ТО ТАКИЕ ТРЕУГОЛЬНИКИ ПОДОБНЫ.
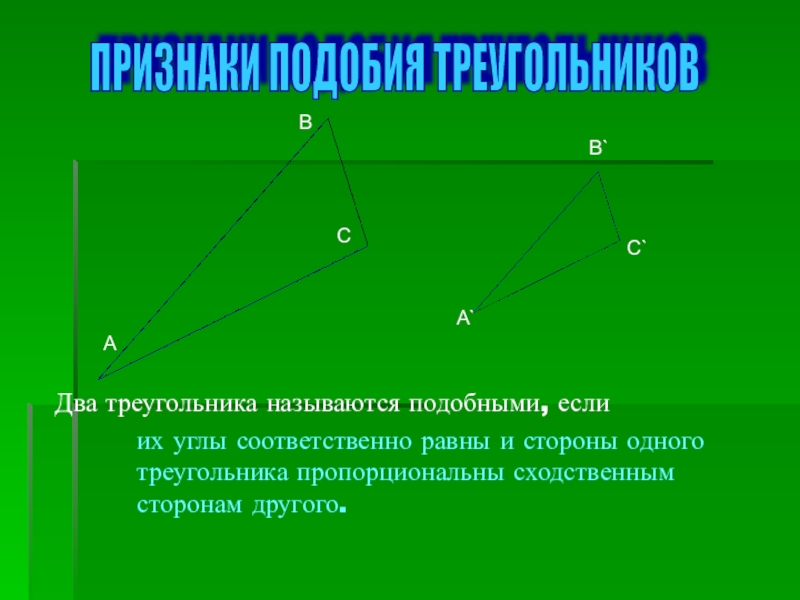
Слайд 1ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ
А
В
С
A`
B`
C`
Два треугольника называются подобными, если
их углы соответственно равны и
Слайд 2Первый признак подобия треугольников
ЕСЛИ ДВА УГЛА ОДНОГО ТРЕУГОЛЬНИКА СООТВЕТСТВЕННО РАВНЫ ДВУМ
УГЛАМ ДРУГОГО, ТО ТАКИЕ ТРЕУГОЛЬНИКИ ПОДОБНЫ.
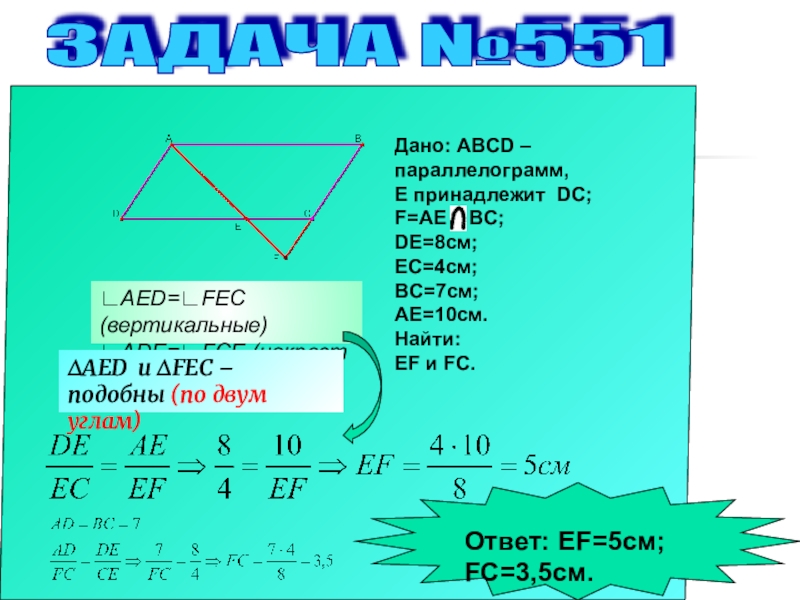
Слайд 3ЗАДАЧА №551
Дано: ABCD –
параллелограмм,
Е принадлежит DC;
F=AE BC;
DE=8см;
EC=4см;
BC=7см;
AE=10см.
Найти:
EF и FC.
∟AED=∟FEC
(вертикальные) ∟ADE=∟FCE (накрест лежащие)
∆AED и ∆FEC – подобны (по двум углам)
Ответ: EF=5см; FC=3,5см.
Слайд 6Второй признак подобия треугольников: Если две стороны одного треугольника пропорциональны двум сторонам
другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
АВ:А`B`=AC:A`C`;
∟A=∟A`
∆ABC ∆A`B`C`
Слайд 7
Задача №559
На одной из сторон данного угла А отложены отрезки
АВ=5см
и АС=16 см. На другой стороне этого же угла
отложены отрезки AD=8см и AF=10см. Подобны ли
треугольники ACD и AFB?
отложены отрезки AD=8см и AF=10см. Подобны ли
треугольники ACD и AFB?
Дано: АВ=5см
АС=16см,AD=8см,
AF=10см.
Найти: ACD и AFB
подобны?
Решение
1) ∟А- общий
∆ACD и ∆AFB
подобны по углу и двум сторонам.
Слайд 8Третий
признак
подобия
Если три стороны одного треугольника пропорциональны
трём сторонам другого, то такие треугольники подобны.
Слайд 9
Треугольники подобны, если
Подобны ли треугольники ABC и A1B1C1, если АВ=3см,
ВС=5см, СА=7см, А1В1=4,5см, В1С1=7,5см, С1А1=10,5см?
Задача №560
Решение
Треугольники подобны, если
Проверим:
Слайд 10
Средняя линия треугольника
Средней линией треугольника называется отрезок, соединяющий середины двух его
сторон.
СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА ПАРАЛЛЕЛЬНА ОДНОЙ ИЗ ЕГО СТОРОН И РАВНА ПОЛОВИНЕ ЭТОЙ СТОРОНЫ.
Дано:
EFG
EH=HF
EI=IG
Доказать:
HI
FG
Слайд 11
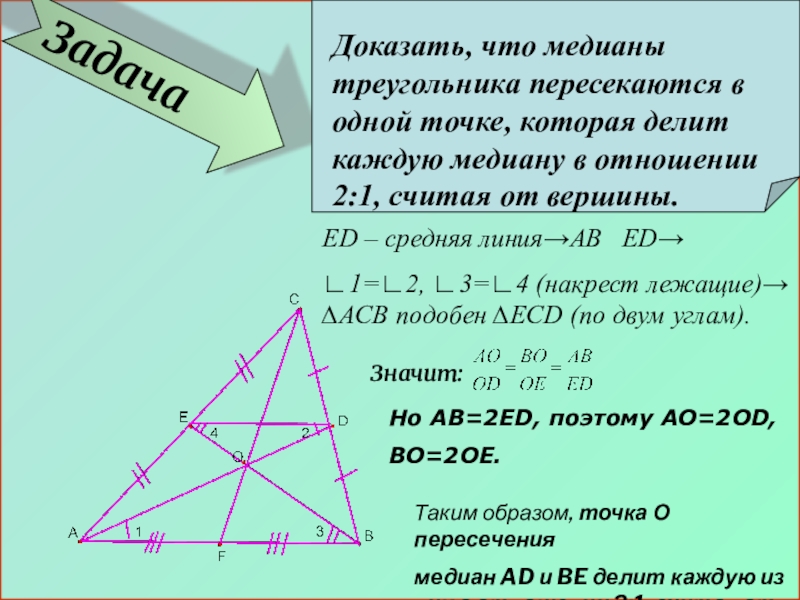
Задача
Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую
медиану в отношении 2:1, считая от вершины.
ED – средняя линия→AB ED→
∟1=∟2, ∟3=∟4 (накрест лежащие)→ ∆ACB подобен ∆ECD (по двум углам).
Значит:
Но AB=2ED, поэтому AO=2OD,
BO=2OE.
Таким образом, точка О пересечения
медиан AD и BE делит каждую из них в отношении 2:1, считая от вершины
Слайд 12
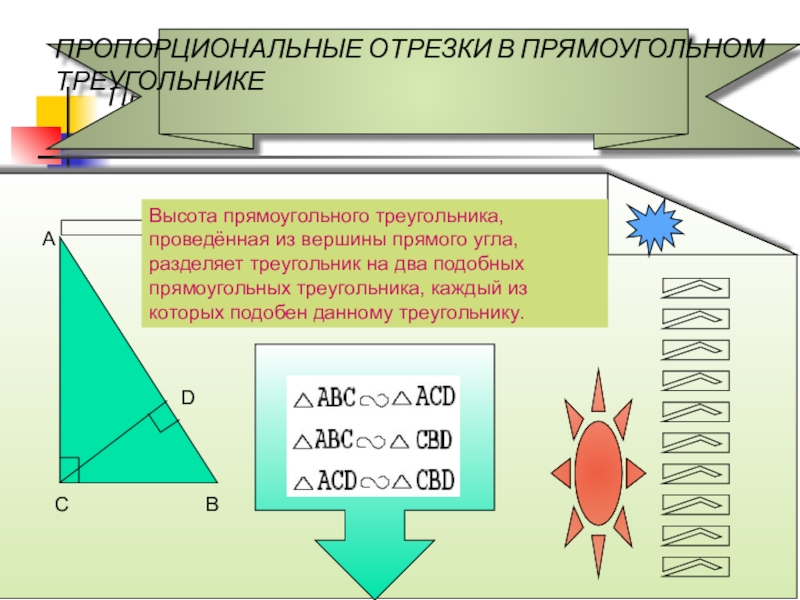
ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ
ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ
А
В
D
Высота прямоугольного треугольника,
проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
С
Слайд 13
1. Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее
пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
А
В
С
D
Слайд 14
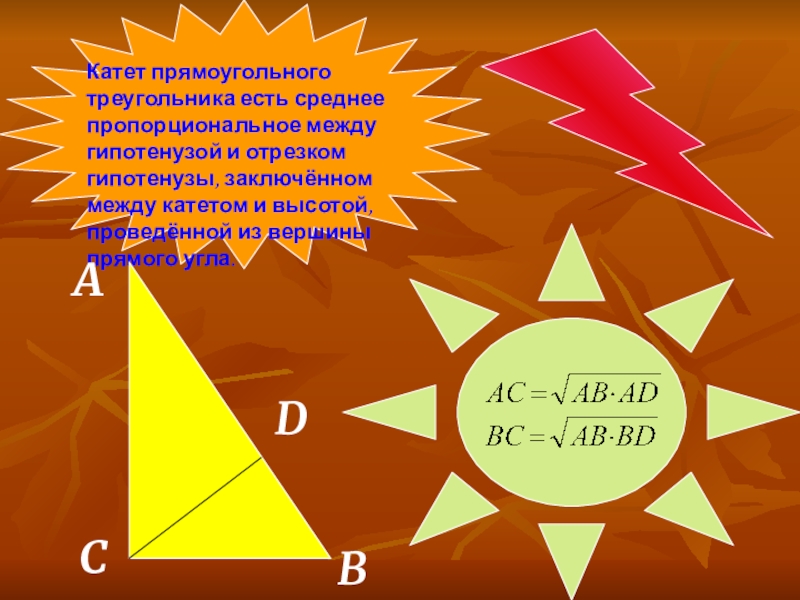
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы,
заключённом между катетом и высотой, проведённой из вершины прямого угла.
А
В
С
D
