- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Правильные многогранники
Содержание
- 1. Презентация к уроку Правильные многогранники
- 2. Определение правильного многогранника:Выпуклый многогранник, у которого все
- 3. Количество правильных многогранников определяется правилом:В выпуклом многограннике сумма плоских углов при каждой вершине меньше 360°
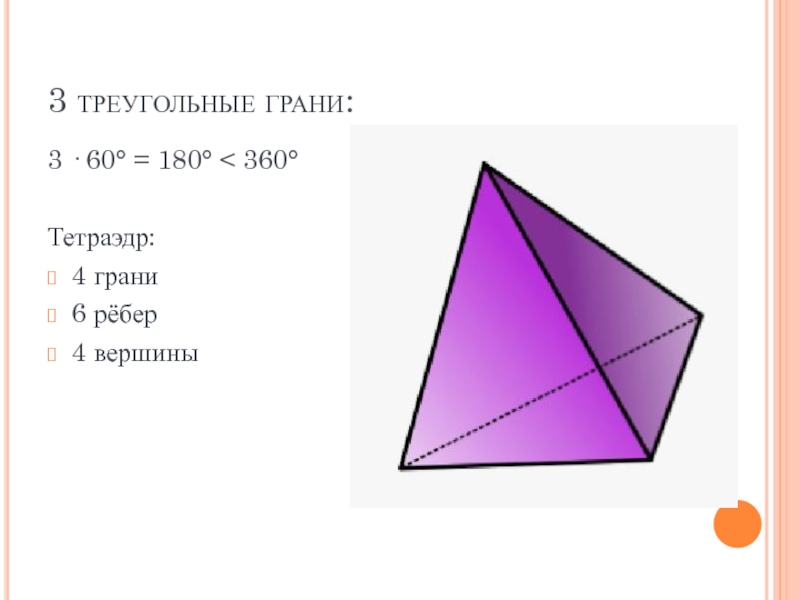
- 4. 3 треугольные грани:3 · 60° = 180° < 360°Тетраэдр:4 грани6 рёбер4 вершины
- 5. 4 треугольные грани:4 · 60° = 240° < 360°Октаэдр:8 граней12 рёбер6 вершин
- 6. 5 треугольных граней:5 · 60° = 300° < 360°Икосаэдр:20 граней30 рёбер12 вершин
- 7. 6 треугольных граней:6 · 60° = 360°Вывод: такоймногогранникневозможен
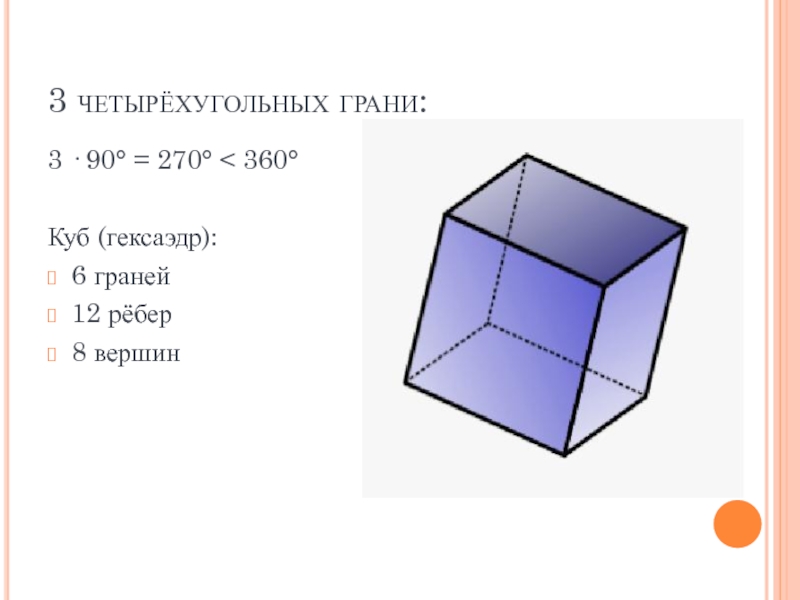
- 8. 3 четырёхугольных грани:3 · 90° = 270° < 360°Куб (гексаэдр):6 граней12 рёбер8 вершин
- 9. 4 четырёхугольных грани:4 · 90° = 360°Вывод: такоймногогранникневозможен
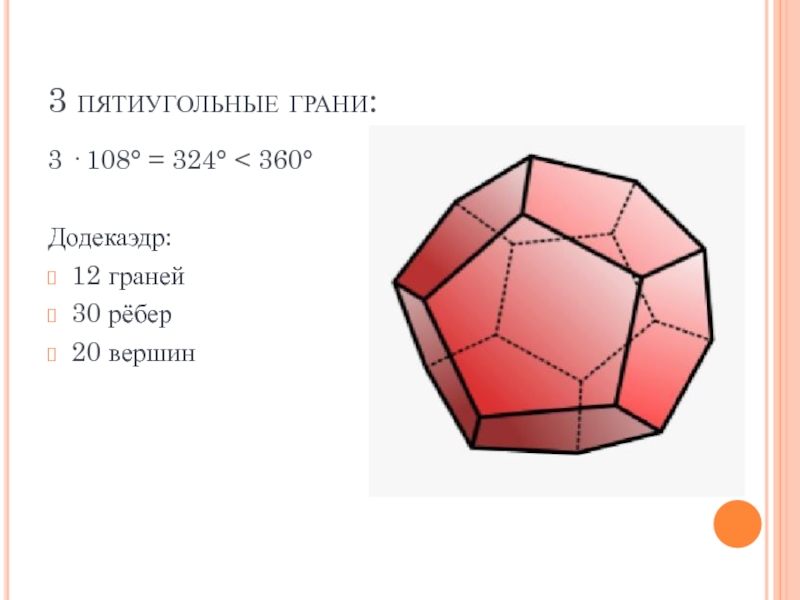
- 10. 3 пятиугольные грани:3 · 108° = 324° < 360°Додекаэдр:12 граней30 рёбер20 вершин
- 11. 4 пятиугольные грани:4 · 108° = 432° > 360°Вывод: такоймногогранникневозможен
- 12. 3 шестиугольных грани:3 · 120° = 360°Следовательно,
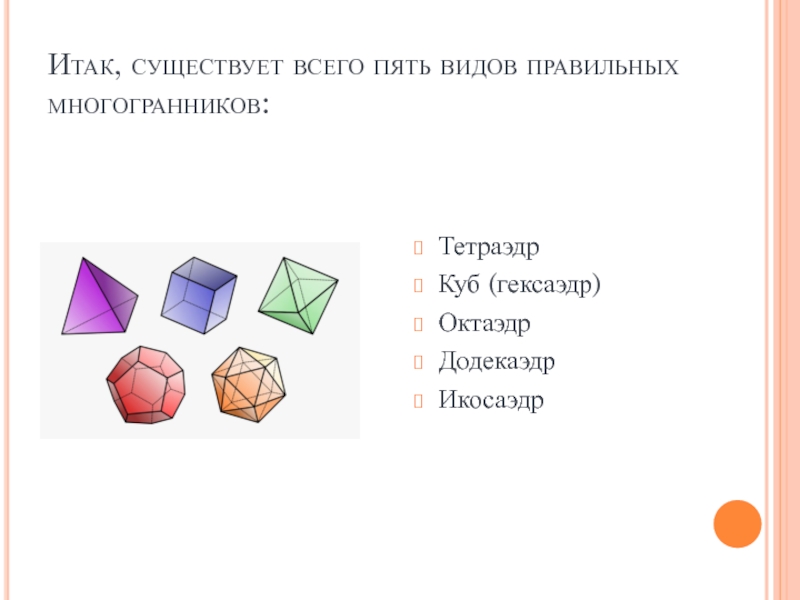
- 13. Итак, существует всего пять видов правильных многогранников:ТетраэдрКуб (гексаэдр)ОктаэдрДодекаэдрИкосаэдр
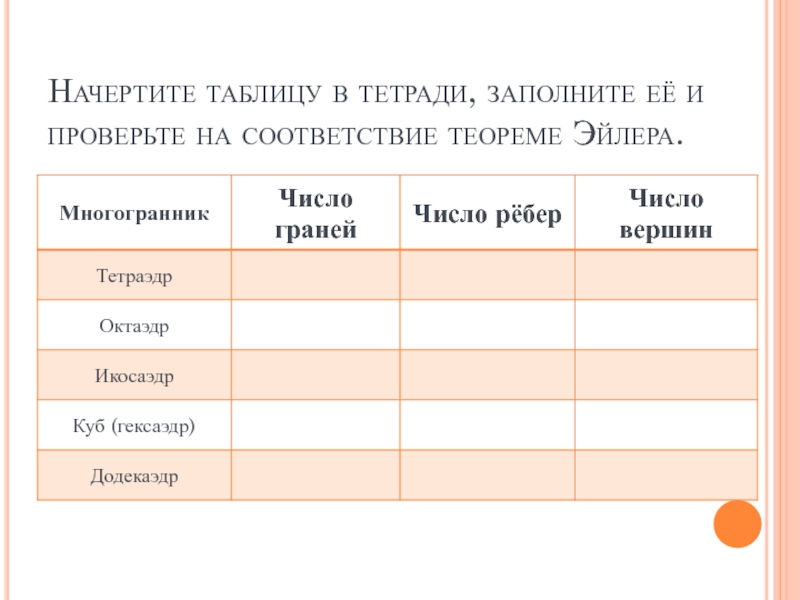
- 14. Начертите таблицу в тетради, заполните её и проверьте на соответствие теореме Эйлера.
Определение правильного многогранника:Выпуклый многогранник, у которого все грани – равные правильные многоугольники, и в каждой вершине сходится одинаковое количество рёбер.
Слайд 1Правильные многогранники
презентация к уроку
Выполнил
Максимов С.В.
преподаватель математики
ГБПОУ Садово-архитектурный колледж, С-Пб
Слайд 2Определение правильного многогранника:
Выпуклый многогранник, у которого все грани – равные правильные
многоугольники, и в каждой вершине сходится одинаковое количество рёбер.
Слайд 3Количество правильных многогранников определяется правилом:
В выпуклом многограннике сумма плоских углов при
каждой вершине меньше 360°
Слайд 123 шестиугольных грани:
3 · 120° = 360°
Следовательно, правильного многогранника с шестиугольными,
семиугольными и вообще n-угольными гранями при n>5 – не существует.