- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии Вписанные и описанные окружности
Содержание
- 1. Презентация к уроку геометрии Вписанные и описанные окружности
- 2. Понятие окружности Окружностью называется фигура, состоящая из множества
- 3. Центральные и вписанные углыУгол с вершиной в
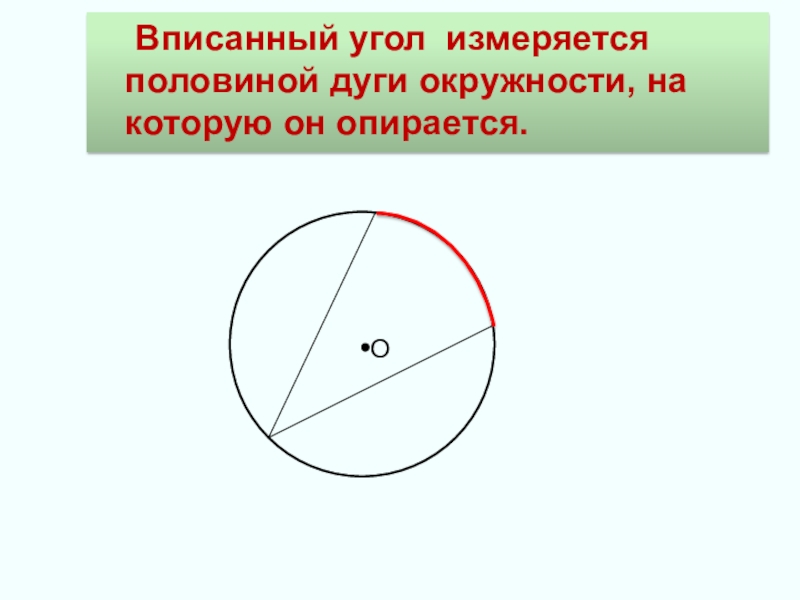
- 4. Вписанный угол измеряется половиной дуги окружности, на которую он опирается.О
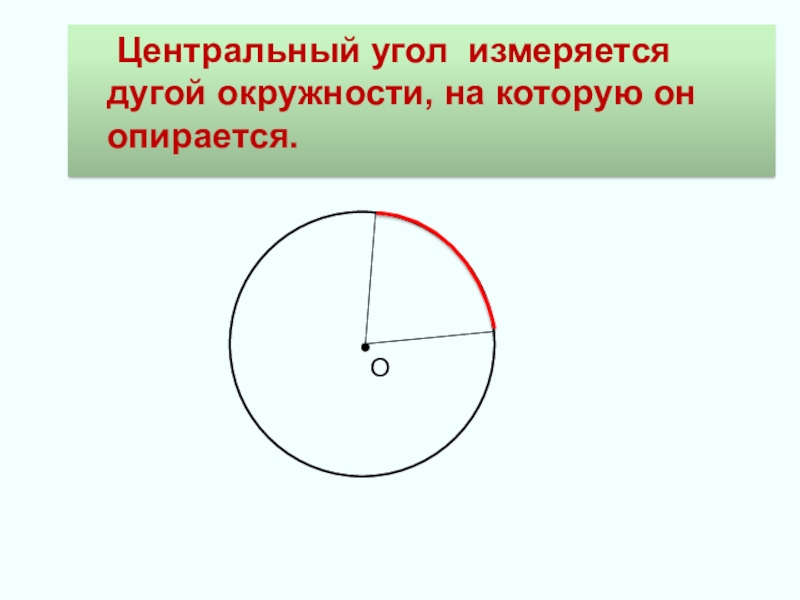
- 5. О Центральный угол измеряется дугой окружности, на которую он опирается.
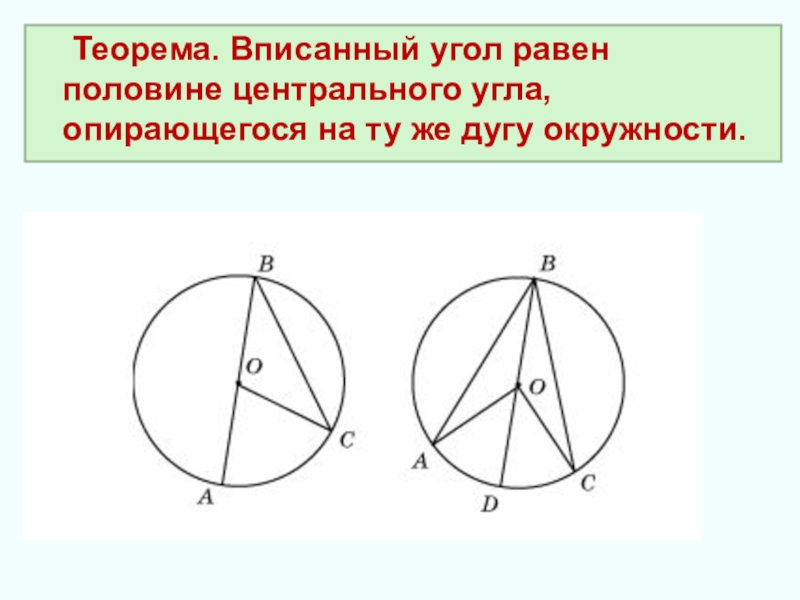
- 6. Теорема. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу окружности.
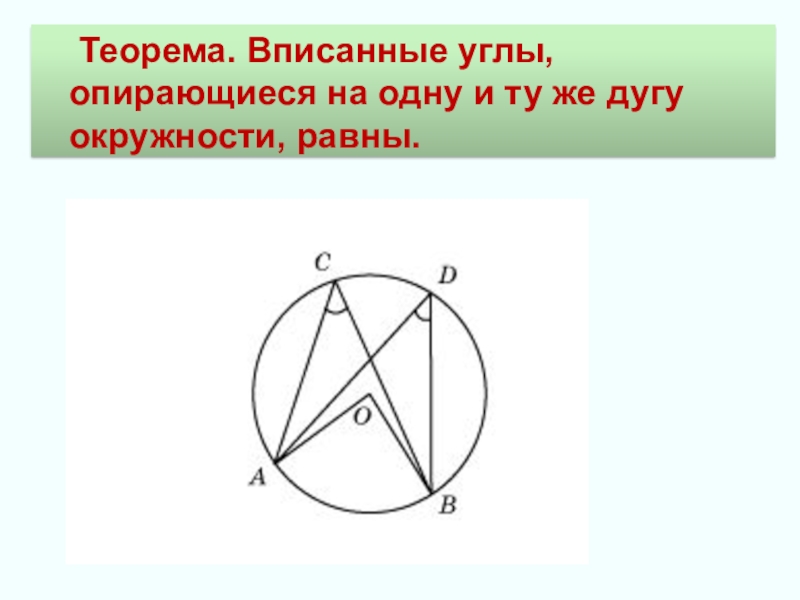
- 7. Теорема. Вписанные углы, опирающиеся на одну и ту же дугу окружности, равны.
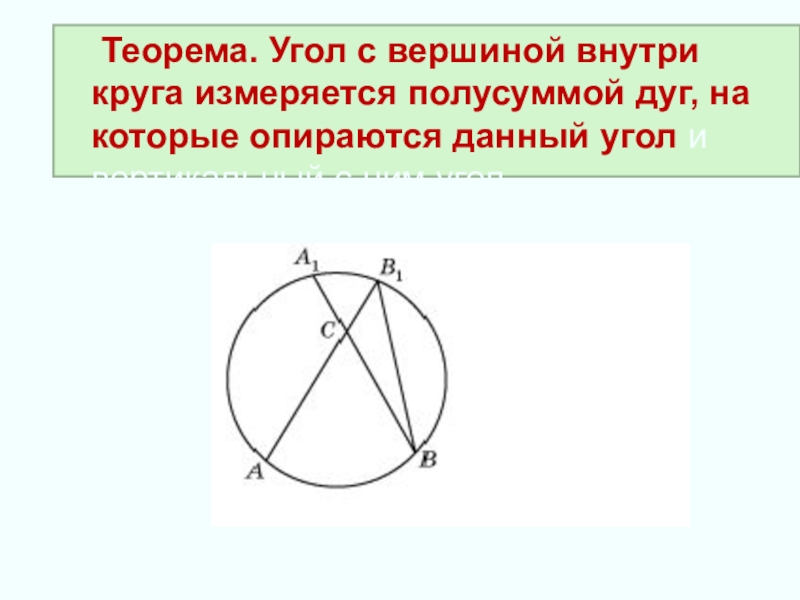
- 8. Теорема. Угол с вершиной внутри круга измеряется
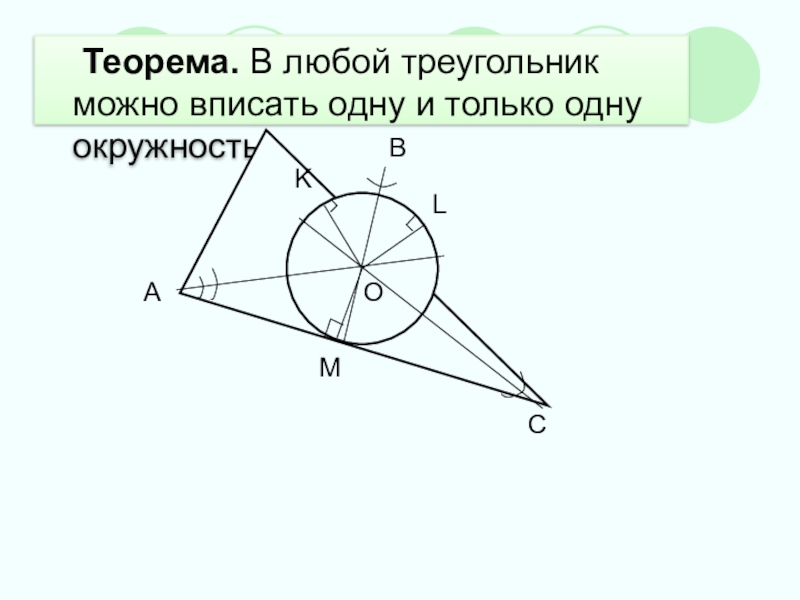
- 9. Теорема. В любой треугольник можно вписать одну и только одну окружность.BАKLCMO
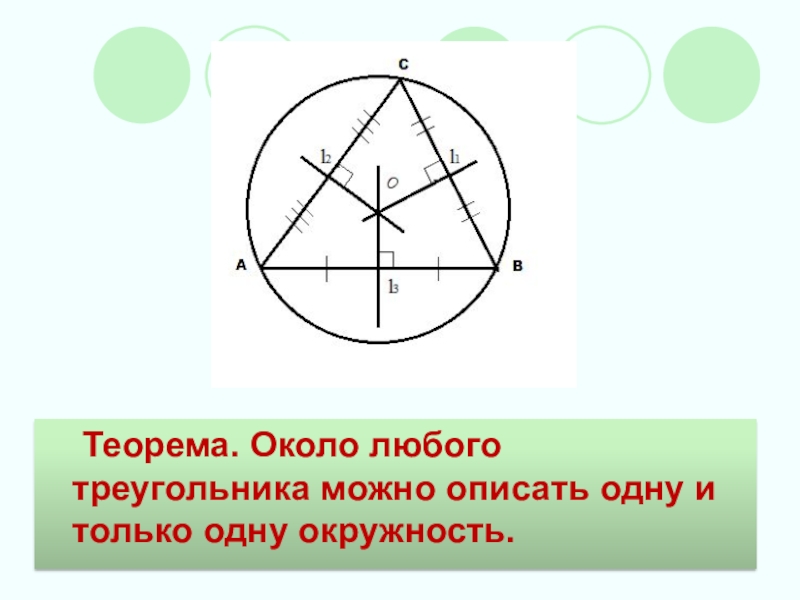
- 10. Теорема. Около любого треугольника можно описать одну и только одну окружность.
- 11. Формулы для вычисления площади треугольника S этого треугольника вычисляется по формулам:S = pr ABCabcRrp = (a+b+c)/2
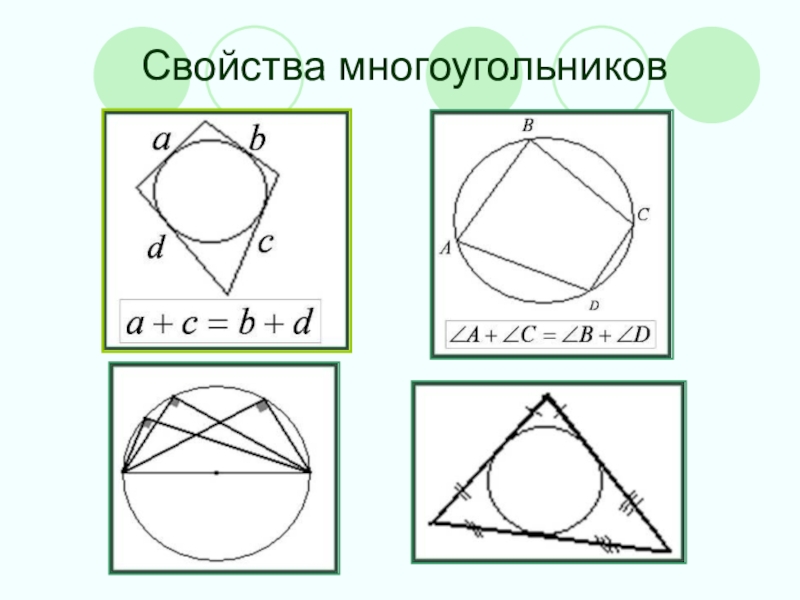
- 12. Свойства многоугольников
- 13. Устные упражнения
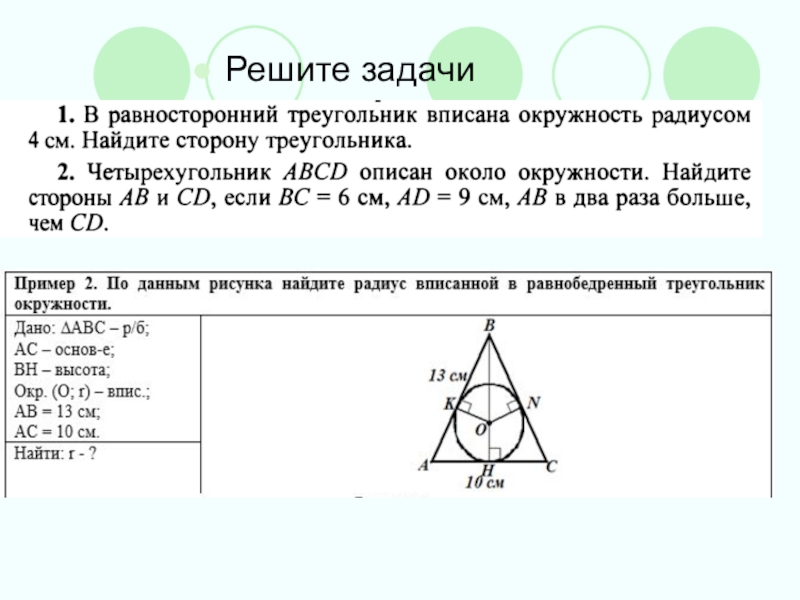
- 14. Решите задачи
- 15. Домашнее задание1. В прямоугольный треугольник с гипотенузой
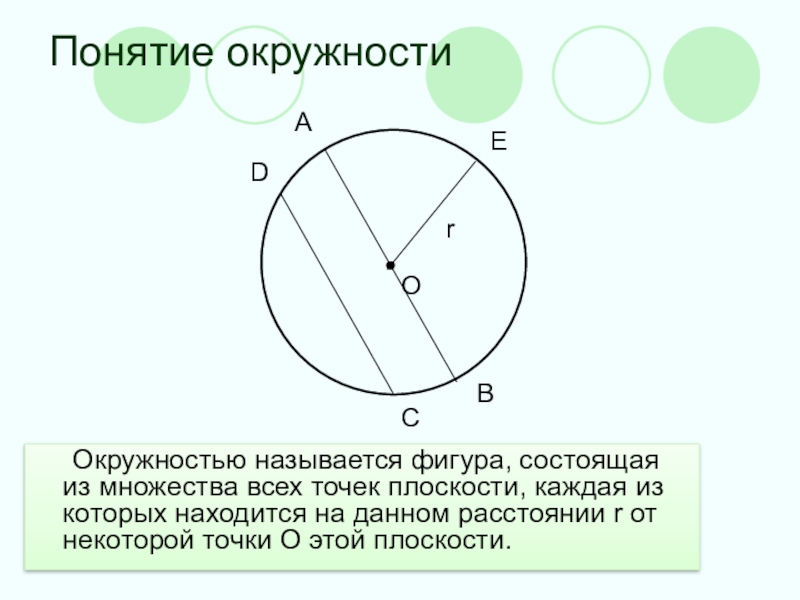
Понятие окружности Окружностью называется фигура, состоящая из множества всех точек плоскости, каждая из которых находится на данном расстоянии r от некоторой точки О этой плоскости. ОАВDCEr
Слайд 2Понятие окружности
Окружностью называется фигура, состоящая из множества всех точек плоскости, каждая
из которых находится на данном расстоянии r от некоторой точки О этой плоскости.
О
А
В
D
C
E
r
Слайд 3
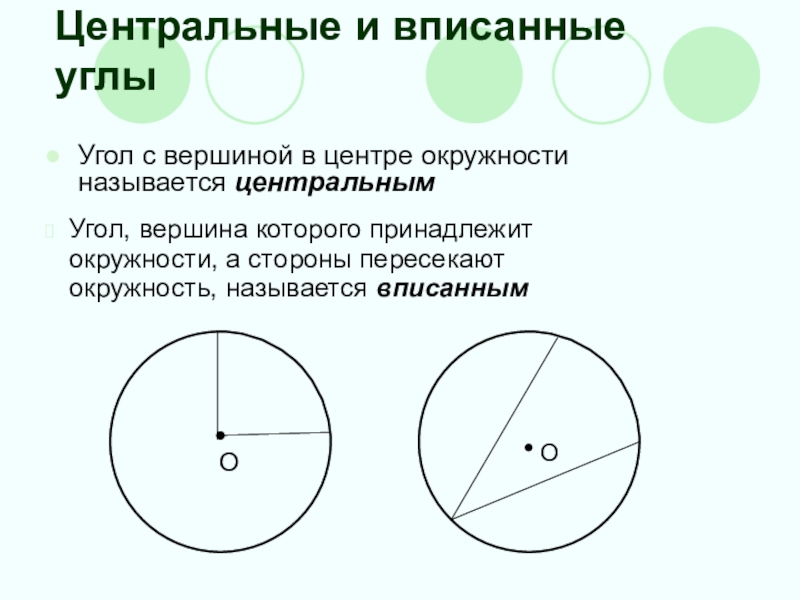
Центральные и вписанные углы
Угол с вершиной в центре окружности называется центральным
Угол, вершина которого принадлежит окружности, а стороны пересекают окружность, называется вписанным
О
О
Слайд 6 Теорема. Вписанный угол равен половине центрального угла, опирающегося на ту же
дугу окружности.
Слайд 8 Теорема. Угол с вершиной внутри круга измеряется полусуммой дуг, на которые
опираются данный угол и вертикальный с ним угол.
Слайд 11
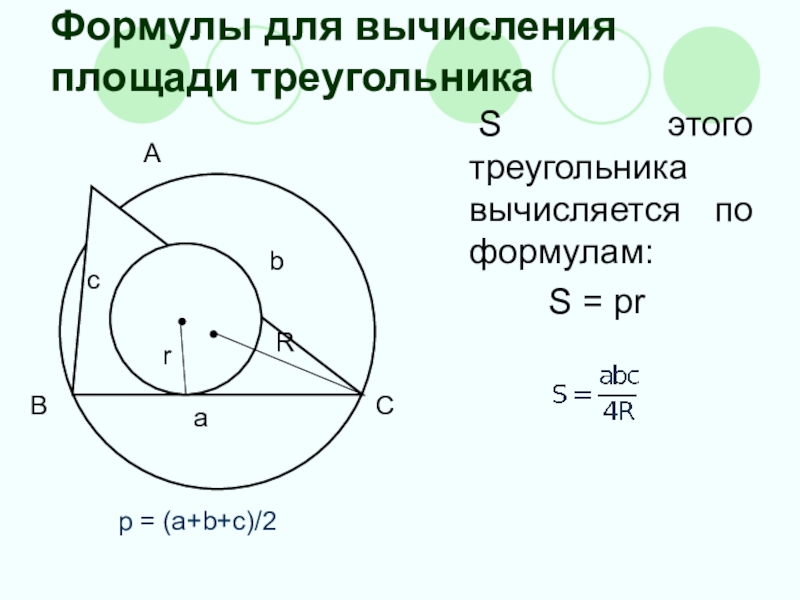
Формулы для вычисления площади треугольника
S этого треугольника вычисляется по формулам:
S =
pr
A
B
C
a
b
c
R
r
p = (a+b+c)/2
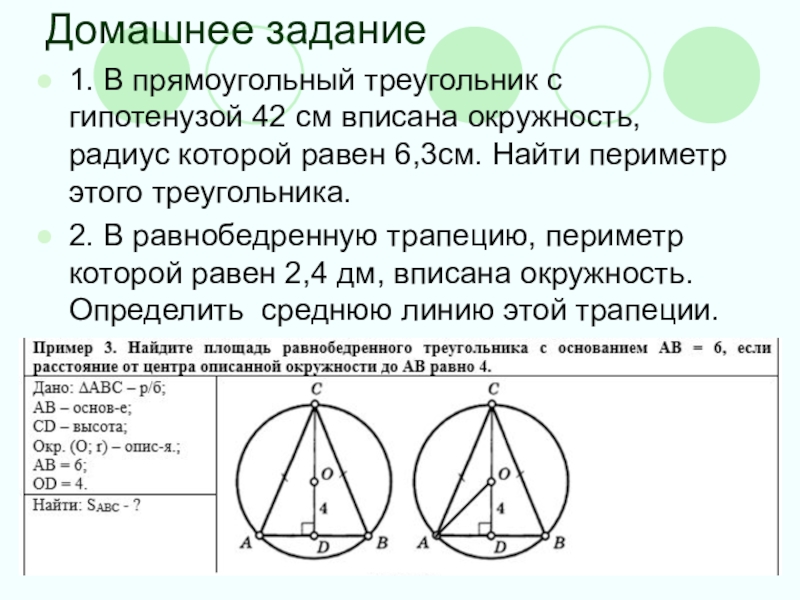
Слайд 15Домашнее задание
1. В прямоугольный треугольник с гипотенузой 42 см вписана окружность,
радиус которой равен 6,3см. Найти периметр этого треугольника.
2. В равнобедренную трапецию, периметр которой равен 2,4 дм, вписана окружность. Определить среднюю линию этой трапеции.
2. В равнобедренную трапецию, периметр которой равен 2,4 дм, вписана окружность. Определить среднюю линию этой трапеции.