- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии в 8 классе по теме Теорема Пифагора
Содержание
- 1. Презентация к уроку геометрии в 8 классе по теме Теорема Пифагора
- 2. Устная работа1. Определите вид треугольника, изображённого на
- 3. Устная работа1. Перечислите фигуры, изображенные на рисунке.2.
- 4. Практическая работа (Эксперимент)1. Изобразите в тетради прямоугольный
- 5. Формулировка теоремы Пифагора В
- 6. Доказательство т. Пифагора1. Достроим треугольник до
- 7. Для запоминания т. Пифагора Если
- 8. Исторические сведения о Пифагоре1. Пифагор –
- 9. Пифагор и пифагорейцыШкола просуществовала до начала IV
- 10. История теоремы Пифагора Хотя эта теорема
- 11. Теорема Пифагора при решении задач Задача
- 12. Теорема Пифагора при решении задач Задача
- 13. Проверочная работаВариант № 1.1. В прямоугольном треугольнике
- 14. Ключ к проверочной работеВариант № 1.1.
- 15. Применение теоремы ПифагораТеорема Пифагора замечательна тем,
- 16. Значение теоремы Пифагора Теорема
- 17. Домашнее задание §3, п. 54, вопрос 8
- 18. Рефлексиясегодня я узнал…теперь я могу…я научился…раньше я не знал, что…меня удивило…было интересно…было трудно…я понял, что…
- 19. Список использованных источников: Учебник «Геометрия» 7-9 кл., Атанасян Л.С., -М.: Просвещение.2. http://www.univer.omsk.su/omsk/Edu/Math/ppifagor.jpg3. http://www.abc-people.com/data/rafael-santi/pic-8b.jpg4. https://ru.wikipedia.org
Слайд 1
Урок по теме
«Теорема Пифагора»
Урок в 8 классе
МБОУ СОШ №
Жила А.Н.,
учитель математики
Слайд 2Устная работа
1. Определите вид треугольника, изображённого на рисунке.
2. Назовите его стороны.
3. Как найти площадь этого треугольника?
а с
в
Слайд 3Устная работа
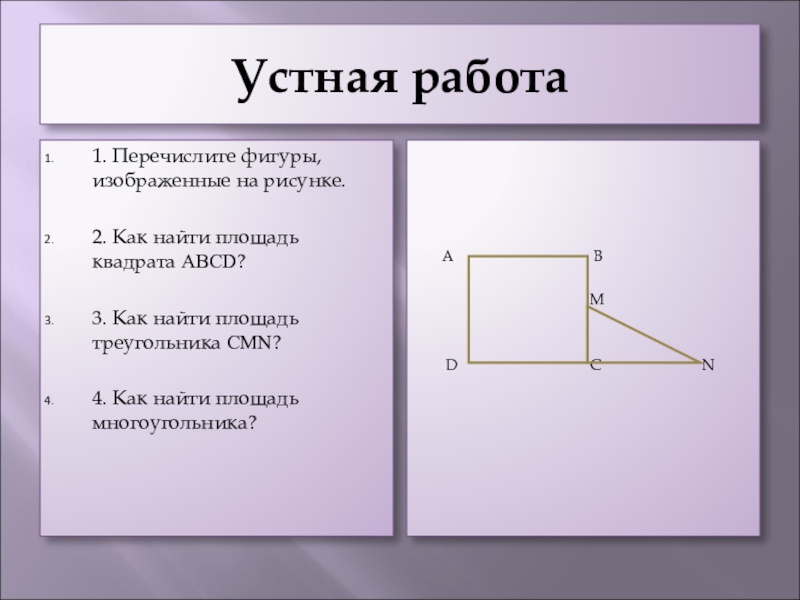
1. Перечислите фигуры, изображенные на рисунке.
2. Как найти площадь квадрата
3. Как найти площадь треугольника CMN?
4. Как найти площадь многоугольника?
A B
M
D C N
Слайд 4Практическая работа (Эксперимент)
1. Изобразите в тетради прямоугольный треугольник с катетами a,
2. Измерьте катеты a, b и гипотенузу c. Результаты запишите в таблицу.
3. Найдите квадраты полученных величин a, b и c. Результаты запишите в таблицу.
4. Найдите сумму a² + b². Результат запишите в таблицу.
5. Сравните полученный результат с квадратом гипотенузы c².
6. Сделайте вывод.
Слайд 5Формулировка
теоремы Пифагора
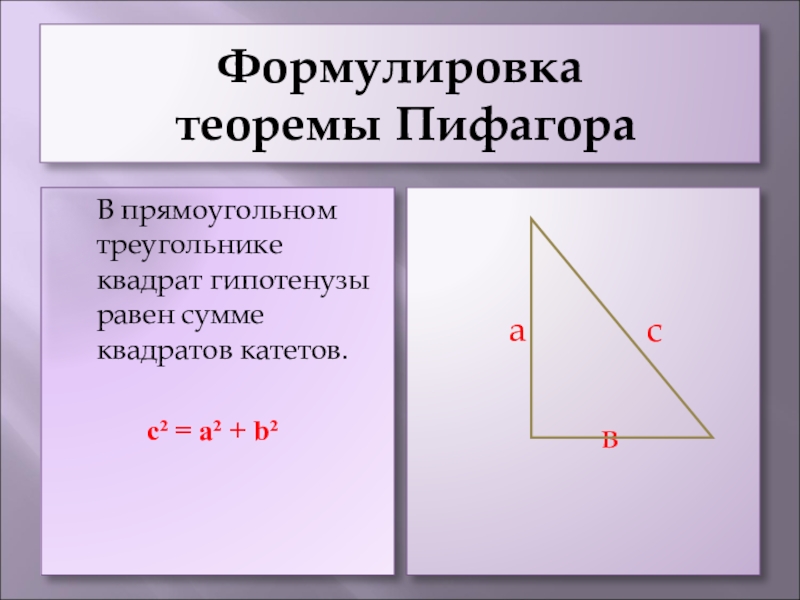
В прямоугольном треугольнике квадрат гипотенузы равен
c² = a² + b²
а с
в
Слайд 6 Доказательство т. Пифагора
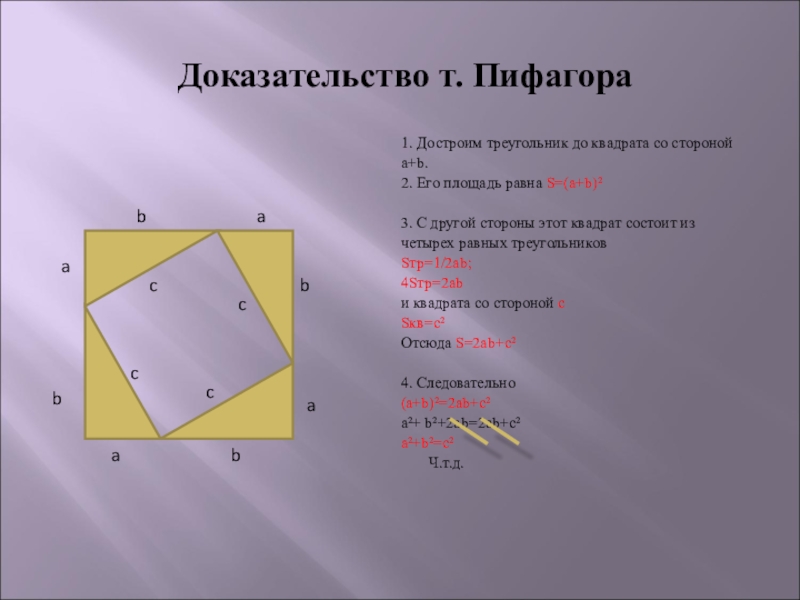
1. Достроим треугольник до квадрата со стороной
a+b.
2. Его площадь равна S=(a+b)²
3. С другой стороны этот квадрат состоит из
четырех равных треугольников
Sтр=1/2ab;
4Sтр=2ab
и квадрата со стороной с
Sкв=с²
Отсюда S=2ab+c²
4. Следовательно
(a+b)²=2ab+c²
a²+ b²+2ab=2ab+c²
a²+b²=c²
Ч.т.д.
a
b
c
a
b
c
c
c
a
a
b
b
Слайд 7Для запоминания т. Пифагора
Если дан нам треугольник
И притом
Слайд 8Исторические сведения
о Пифагоре
1. Пифагор – великий древнегреческий ученый, живший в
2. Среди учителей юного Пифагора традиционно называют имена старца Гермодаманта и Ферекида Сиросского (хотя твердой уверенности в этом нет).
3. О жизни Пифагора известно немного, но с его именем связано множество легенд. Рассказывают, что он много путешествовал, был в Индии, Египте, Вавилоне, изучал древнюю культуру и достижения науки разных стран.
4. Вернувшись на родину, Пифагор организовал кружок молодёжи из представителей аристократии. В кружок принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Так, на юге Италии, которая тогда была греческой колонией, возникла так называемая пифагорейская школа.
Слайд 9Пифагор и пифагорейцы
Школа просуществовала до начала IV в. до н.э., хотя
По сути, это была первая философская школа, религиозно-философское аристократическое братство; она имела большое влияние на греческие полисы Южной Италии и Сицилии.
Союз отличался строгими обычаями и высокой нравственностью. Образ жизни пифагорейцев вошел в историю: как рассказывают легенды, учеников Школы всегда можно было узнать по их внешнему облику и благородному поведению.
Пифагорейская школа положила начало математическим наукам. В пифагорейской школе начали развиваться астрономия и медицина.
Слайд 10История теоремы Пифагора
Хотя эта теорема и связывается с именем
Сохранилось древнее предание, что в честь своего открытия Пифагор принёс в жертву богам быка, по другим свидетельствам – даже сто быков. Но это противоречит сведениям о моральных и религиозных воззрениях Пифагора. Говорят, что он “запрещал даже убивать животных, а тем более ими кормиться, ибо животные имеют душу, как и мы”. В связи с этим более правдоподобной можно считать следующую запись: “… когда он открыл, что в прямоугольном треугольнике гипотенуза имеет соответствие с катетами, он принес в жертву быка, сделанного из пшеничного теста”.
В настоящее время имеется более 200 различных доказательств этой теоремы. Значение её состоит в том, что из неё или с её помощью можно вывести большинство теорем геометрии. Доказательство теоремы учащиеся средних веков считали очень трудными. Ученики рисовали шаржи на теорему Пифагора.
Слайд 11Теорема Пифагора
при решении задач
Задача № 1. В прямоугольном треугольнике
А
5 ?
С В
12
Решение.
По теореме Пифагора
АВ² = АС² + ВС².
АВ² = 5² + 12²;
АВ² = 25 + 144;
АВ² = 169;
Значит, АВ = 13 (см).
Слайд 12Теорема Пифагора
при решении задач
Задача № 2. В прямоугольном треугольнике
А
5 13
С В
?
Решение.
По теореме Пифагора
АВ² = АС² + ВС².
ВС² = АВ² - АС²;
ВС² = 13² - 12²;
ВС² = 169 - 144;
ВС² = 25;
Значит, ВС = 5 (см).
Слайд 13Проверочная работа
Вариант № 1.
1. В прямоугольном треугольнике АВС угол С равен
2. В прямоугольном треугольнике АВС с прямым углом С катет АС равен 6 см, гипотенуза АВ равна 10 см. Найдите длину катета ВС.
3. В прямоугольнике ABCD диагональ АС равна 5 дм, одна из сторон равна 3 см. Найдите длину другой стороны прямоугольника.
Вариант № 2.
1. В прямоугольном треугольнике АВС с прямым углом С катеты равны 6 см и 8 см. Найдите гипотенузу.
2. В прямоугольном треугольнике АВС угол С прямой, катет ВС равен 20 см, гипотенуза АВ равна 25 см. Найдите длину катета АС.
3. Стороны прямоугольника ABCD равны 3 см и 4 см. Найдите длину диагонали прямоугольника.
Слайд 14Ключ
к проверочной работе
Вариант № 1.
1. АВ = 25 см.
2. ВС
3. 4 см.
Вариант № 2.
1. АВ = 10 см.
2. АС = 15 см.
3. 5 см.
Слайд 15Применение
теоремы Пифагора
Теорема Пифагора замечательна тем, что она проста, но не
Слайд 16Значение
теоремы Пифагора
Теорема Пифагора – одна из главных
О теореме Пифагора.
Суть истины вся в том, что нам она - навечно,
Когда хоть раз в прозрении увидим свет,
И теорема Пифагора через столько лет
Для нас, как для него, бесспорна, безупречна
На радостях богам был дан обет:
За то, что мудрости коснулся бесконечной
Он сто быков заклал благодаря предвечных;
Моленья и хвалы вознес он жертве вслед.
Слайд 17Домашнее задание
§3, п. 54, вопрос 8 на стр. 129;
№483(б),
Творческое задание: найди различные доказательства теоремы Пифагора, выбрать одно понравившееся и представить в классе.
Слайд 18Рефлексия
сегодня я узнал…
теперь я могу…
я научился…
раньше я не знал, что…
меня удивило…
было
было трудно…
я понял, что…
Слайд 19Список использованных источников:
Учебник «Геометрия» 7-9 кл., Атанасян Л.С., -М.: Просвещение.
2.
3. http://www.abc-people.com/data/rafael-santi/pic-8b.jpg
4. https://ru.wikipedia.org