- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии в 7 классе по теме Второй признак равенства треугольников
Содержание
- 1. Презентация к уроку геометрии в 7 классе по теме Второй признак равенства треугольников
- 2. Цель урокаПовторение и закрепление 1 признака равенства
- 3. I этап. Актуализация опорных знаний учащихсяРешение задач
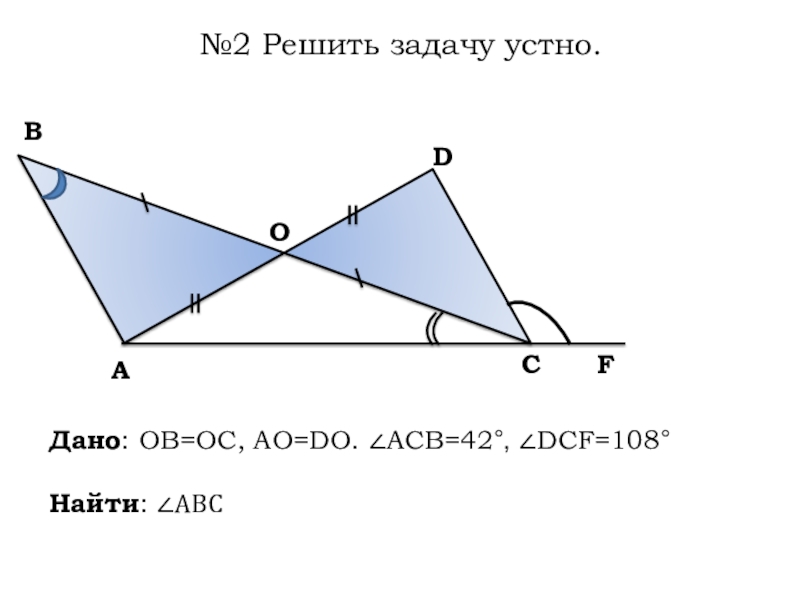
- 4. №2 Решить задачу устно. DABCOFДано: OB=OC, AO=DO. ∠ACB=42°, ∠DCF=108°Найти: ∠ABC∠
- 5. II этап. Изучение нового материала. Практическая работа
- 6. Дано: ∆ ABC, ∆MNK, AB=MN, ∠A =
- 7. Мы доказали второй признак равенства треугольниковСформулируйте его.Теорема:
- 8. Решение задач по готовым чертежам (устно)ABCDABCDEДано:∠1=∠2, ∠3=∠4Докажите: ∆ABC =∆ADC1234Дано:AC=CB, ∠A = ∠BДокажите: ∆BCD =∆ACE№ 2№ 1
- 9. Решение задач по готовым чертежам (устно)12ACBDO№ 4№
- 10. Решение задачи записать в тетрадь№ 127ABCA1B1C1D1DДано: ∆ABC,
- 11. Домашнее задание: выучить доказательство теоремы из п.19;
Слайд 1Второй признак равенства треугольников
Учитель математики Пашко Н.П.
МБОУ «Октябрьская школа-гимназия»
Красногвардейского района республики
Слайд 2Цель урока
Повторение и закрепление 1 признака равенства треугольников
Изучение 2 признака равенства
Выработка навыков использования первого и второго признаков при решении задач
Способствовать развитию логического мышления
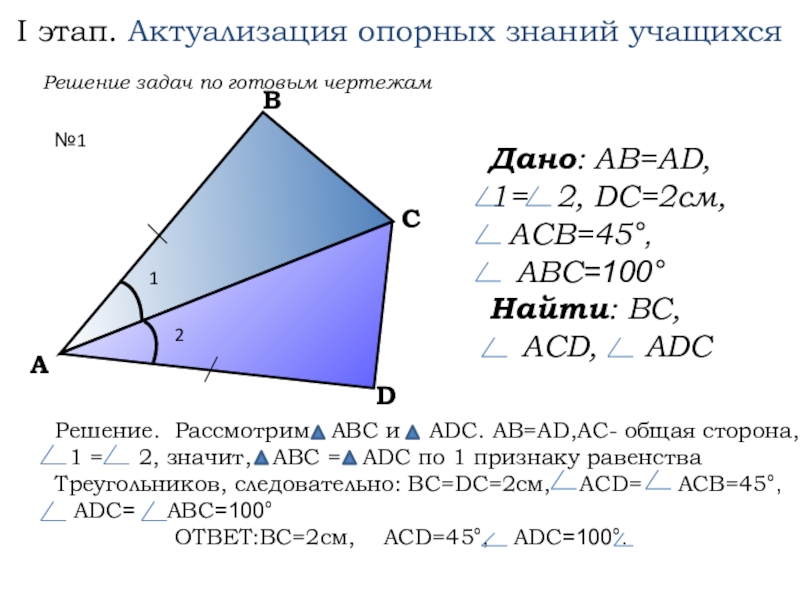
Слайд 3I этап. Актуализация опорных знаний учащихся
Решение задач по готовым чертежам
№1
Дано: АB=AD,
1=
ACB=45°,
ABC=100°
Найти: BC,
ACD, ADC
Решение. Рассмотрим ABC и ADC. AB=AD,AC- общая сторона,
1 = 2, значит, АВС = ADC по 1 признаку равенства
Треугольников, следовательно: BC=DC=2см, ACD= ACB=45°,
ADC= ABC=100°
ОТВЕТ:BC=2см, ACD=45°, ADC=100°.
Слайд 5II этап. Изучение нового материала.
Практическая работа
Начертите ∆MNK- такой, что ∆ MNK=∆
План построения:
Отложить отрезок MN=4см, так как ∆ MNK = ∆ ABC, а значит, MN=AB;
Построить ∠ NMP=54°;
Построить ∠ MNE =46°, по ту же сторону от прямой MN, что и ∠ NMP;
MP ⋂ NQ = K, ∆ MNK - искомый.
Докажем равенство треугольников ABC и MNK
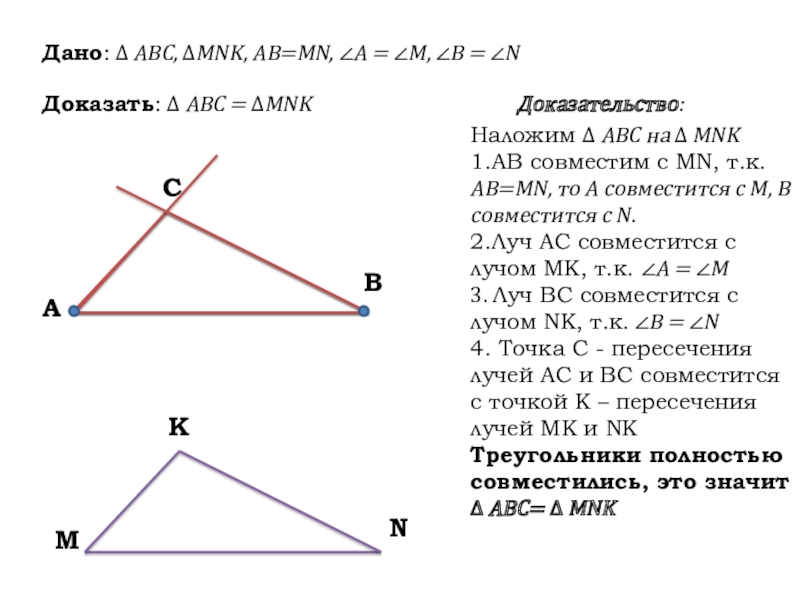
Слайд 6Дано: ∆ ABC, ∆MNK, AB=MN, ∠A = ∠M, ∠B = ∠N
Доказать: ∆ ABC = ∆MNK Доказательство:
A
B
C
Наложим ∆ ABC на ∆ MNK
1.AB совместим с MN, т.к. AB=MN, то А совместится с М, В совместится с N.
2.Луч AC совместится с лучом MK, т.к. ∠A = ∠M
3. Луч BC совместится с лучом NK, т.к. ∠B = ∠N
4. Точка C - пересечения лучей AC и BC совместится с точкой К – пересечения лучей MK и NK
Треугольники полностью совместились, это значит ∆ ABC= ∆ MNK
Слайд 7Мы доказали второй признак равенства треугольников
Сформулируйте его.
Теорема: Если сторона и два
Второй признак равенства треугольников можно называть признаком равенства треугольников по стороне и прилежащим к ней углам
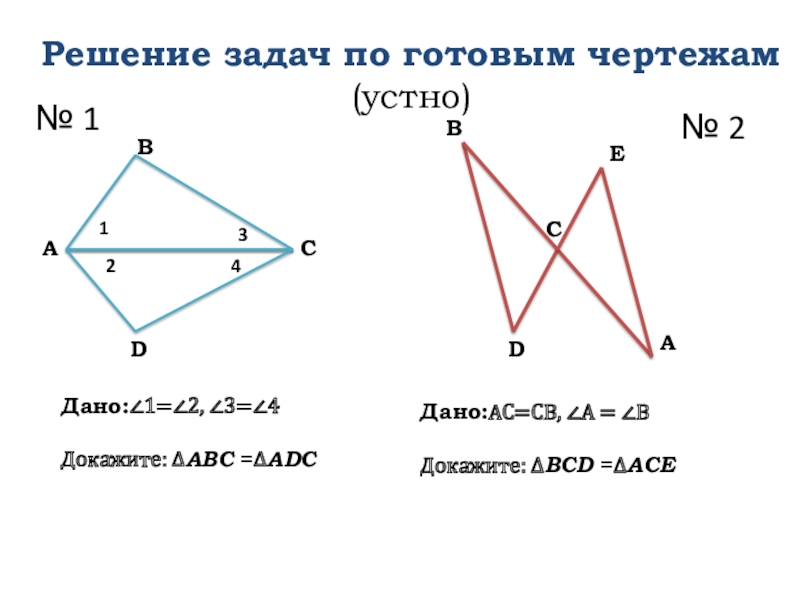
Слайд 8Решение задач по готовым чертежам (устно)
A
B
C
D
A
B
C
D
E
Дано:∠1=∠2, ∠3=∠4
Докажите: ∆ABC =∆ADC
1
2
3
4
Дано:AC=CB, ∠A =
Докажите: ∆BCD =∆ACE
№ 2
№ 1
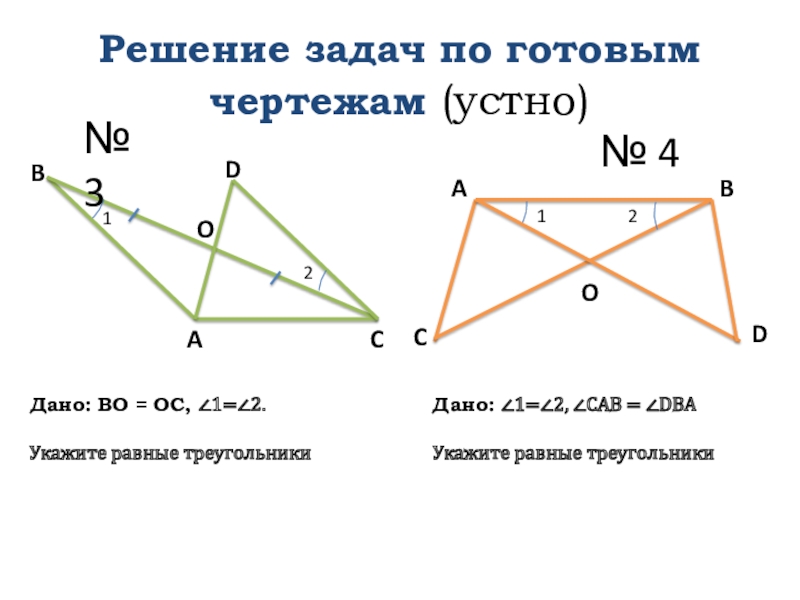
Слайд 9Решение задач по готовым чертежам (устно)
1
2
A
C
B
D
O
№ 4
№ 3
Дано: BO = OC,
Укажите равные треугольники
Дано: ∠1=∠2, ∠CAB = ∠DBA
Укажите равные треугольники
1
2
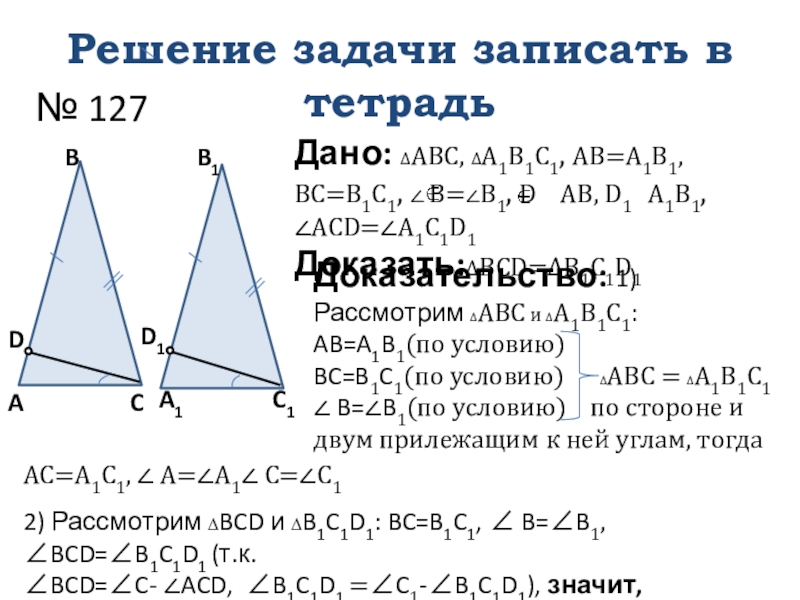
Слайд 10Решение задачи записать в тетрадь
№ 127
A
B
C
A1
B1
C1
D1
D
Дано: ∆ABC, ∆A1B1C1, AB=A1B1, BC=B1C1, ∠
Доказать:∆BCD=∆B1C1D1
Доказательство: 1) Рассмотрим ∆ABC и ∆A1B1C1:
AB=A1B1(по условию)
BC=B1C1(по условию) ∆ABC = ∆A1B1C1
∠ B=∠B1(по условию) по стороне и двум прилежащим к ней углам, тогда
AC=A1C1, ∠ A=∠A1∠ C=∠C1
2) Рассмотрим ∆BCD и ∆B1C1D1: BC=B1C1, ∠ B=∠B1, ∠BCD=∠B1C1D1 (т.к.
∠BCD=∠C- ∠ACD, ∠B1C1D1 =∠C1-∠B1C1D1), значит, ∆BCD=∆B1C1D1
Слайд 11Домашнее задание: выучить доказательство теоремы из п.19; решить задачи 124,125,128
Что нового
Кто может повторить второй признак равенства треугольников?
Молодцы!