- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии в 7 классе на тему: Некоторые свойства прямоугольных треугольников
Содержание
- 1. Презентация к уроку геометрии в 7 классе на тему: Некоторые свойства прямоугольных треугольников
- 2. Цели урокаповторить определение треугольника, виды треугольников;рассмотреть свойства прямоугольных треугольников;научить решать задачи на применение свойств прямоугольных треугольников.
- 3. Эпиграф урокаКитайская мудрость гласит: «Я слышу -
- 4. Блиц опрос1. Какая фигура называется треугольником.2. Какими
- 5. Вычислите неизвестные углы треугольника.
- 6. Слайд 6
- 7. Физминутка
- 8. Сумма двух острых углов прямоугольного треугольника равна
- 9. Катет прямоугольного треугольника , лежащий против угла
- 10. Доказательство:Если катет прямоугольного треугольника равен половине гипотенузы,
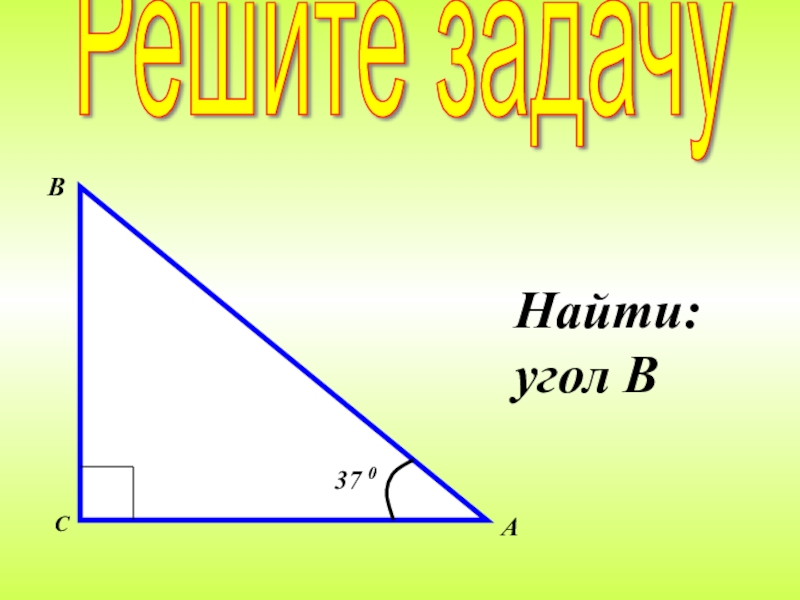
- 11. Найти: угол ВРешите задачу
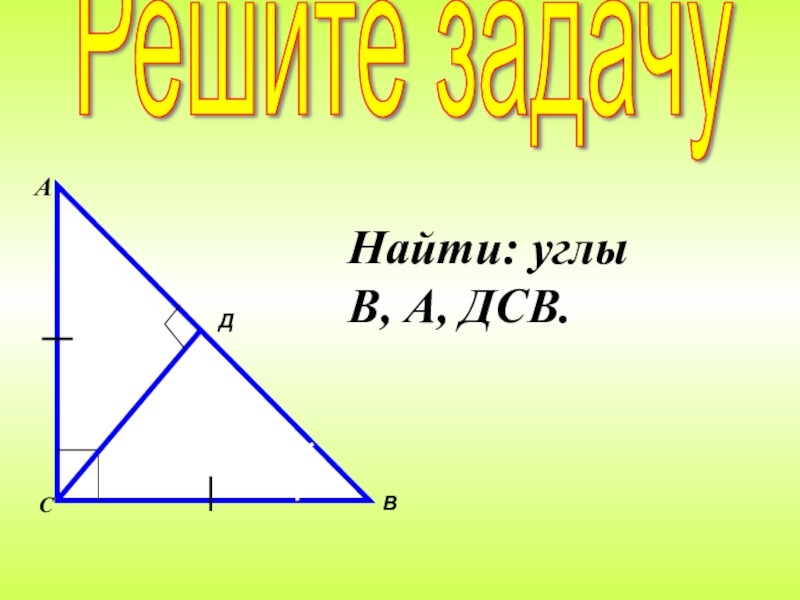
- 12. Найти: углы В, А, ДСВ.Решите задачу
- 13. Найти: Угол САВРешите задачу
- 14. Найти: ВС.Решите задачу
- 15. Задача (№265)В равнобедренном треугольнике ABC с основанием
- 16. -Сумма двух острых углов прямоугольного треугольника равна
- 17. Домашнее заданиеп.34 №255, №256. Творческое задание: сообщение о Пифагоре?
- 18. РефлексияЯ всё понял и могу доказать все
- 19. спасибо за урок!
Слайд 1геометрия 7 класс
Некоторые свойства
прямоугольных треугольников
урок на тему:
Подготовила учитель
Рейн Татьяна Владимировна
Слайд 2Цели урока
повторить определение треугольника, виды треугольников;
рассмотреть свойства прямоугольных треугольников;
научить решать задачи
Слайд 3Эпиграф урока
Китайская мудрость гласит:
«Я слышу - я забываю, я вижу
Слайд 4Блиц опрос
1. Какая фигура называется треугольником.
2. Какими могут быть треугольники в
3. Какой треугольник называется тупоугольным?
4. Может ли в треугольнике быть два тупых угла? Объяснить ответ.
5. Какой угол называется внешним углом треугольника?
6. Каким свойством обладает внешний угол треугольника?
7. Сформулировать теорему о сумме углов треугольника.
8. Какой треугольник называется прямоугольным?
9. Как называются стороны прямоугольного треугольника?
Слайд 8Сумма двух острых углов прямоугольного треугольника равна 90°
Доказательство:
Сумма углов треугольника равна
Свойство 1
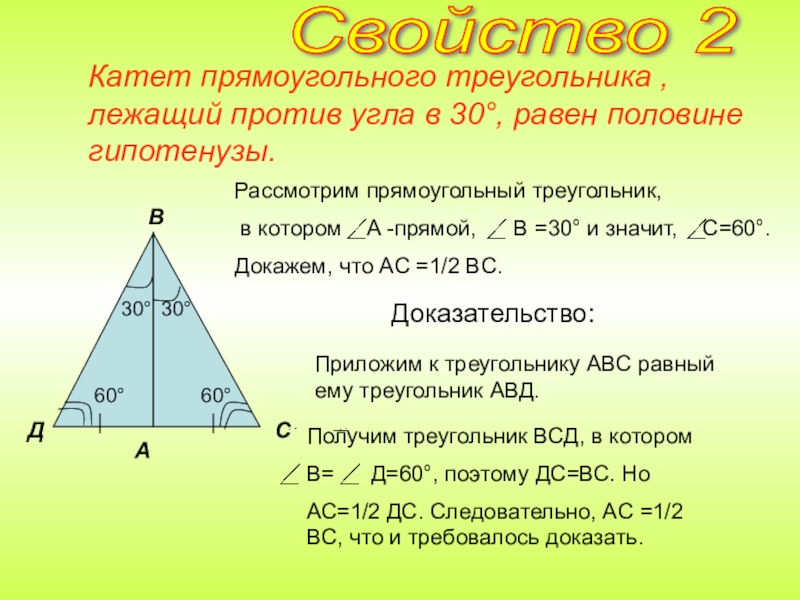
Слайд 9Катет прямоугольного треугольника , лежащий против угла в 30°, равен половине
Доказательство:
Приложим к треугольнику АВС равный ему треугольник АВД.
Свойство 2
Рассмотрим прямоугольный треугольник,
в котором A -прямой, B =30° и значит, C=60°.
Докажем, что AC =1/2 BC.
Получим треугольник ВСД, в котором
В= Д=60°, поэтому ДС=ВС. Но
АС=1/2 ДС. Следовательно, AC =1/2 BC, что и требовалось доказать.
Слайд 10
Доказательство:
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против
Приложим к треугольнику АВС равный ему треугольник АВД.
Получим равносторонний треугольник ВСД. Углы равностороннего треугольника равны друг другу, поэтому каждый из них равен 60°. В частности, ДВС=60°. Но ДВС=2 АВС. Следовательно, АВС=30°, что и требовалось доказать.
Свойство 3
Слайд 15Задача (№265)
В равнобедренном треугольнике ABC с основанием AC проведены биссектриса AF
Решение:
Ответ: 90°, 39° и 51°.
Дано: Δ АВС – равнобедренный, АС - основание, АН – высота, В = 112°.
Найти: углы треугольника AHF.
Слайд 16-Сумма двух острых углов прямоугольного
треугольника равна 90°
Подведение итогов
-Сумма двух острых
треугольника равна 90°
-Катет прямоугольного треугольника ,
лежащий против угла в 30°, равен половине гипотенузы.
-Если катет прямоугольного треугольника равен половине гипотенузы, то угол,
лежащий против этого катета, равен 30°.
Слайд 18Рефлексия
Я всё понял и могу доказать все свойства.
Я всё понял и
Для полного понимания мне необходимо повторить тему дома.
Я ничего не понял.