- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
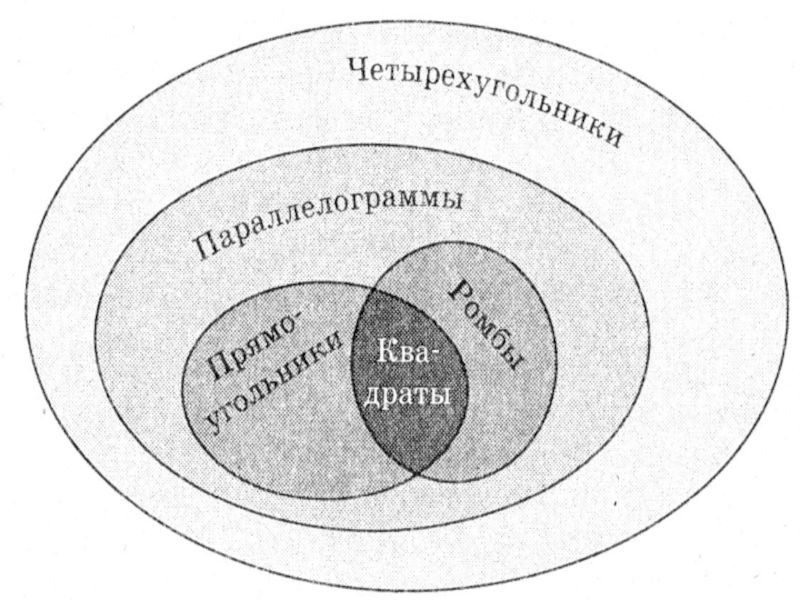
Презентация, доклад к уроку Четырёхугольники
Содержание
- 1. Презентация к уроку Четырёхугольники
- 2. Цель: обобщить основные теоретические сведения о параллелограмме,
- 3. № 1 только две противолежащие стороны параллельны. МБОУ Водопойненская средняя школаОтветтрапеция.
- 4. №2 противолежащие стороны параллельны.МБОУ Водопойненская средняя школаОтвет:параллелограмм
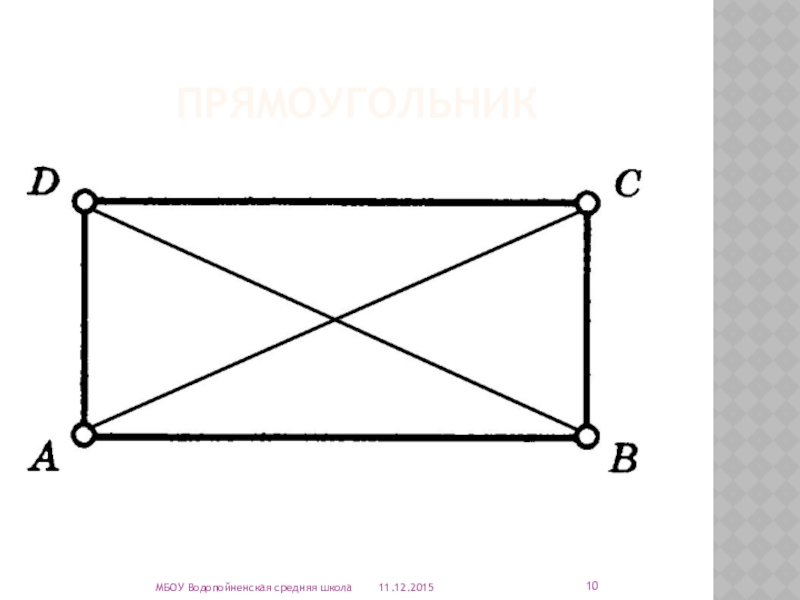
- 5. прямоугольник№ 3 противолежащие стороны параллельны и все углы прямые.МБОУ Водопойненская средняя школаОтвет:
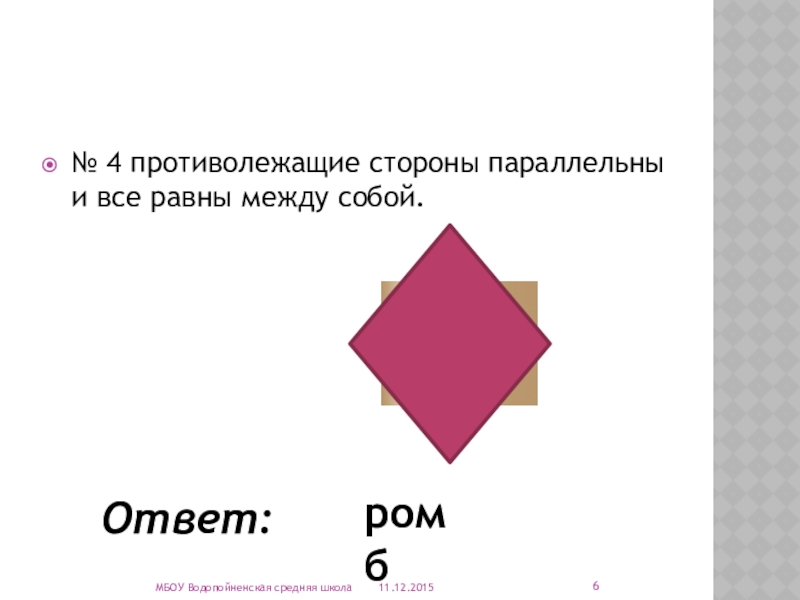
- 6. № 4 противолежащие стороны параллельны и все равны между собой.МБОУ Водопойненская средняя школаОтвет:ромб
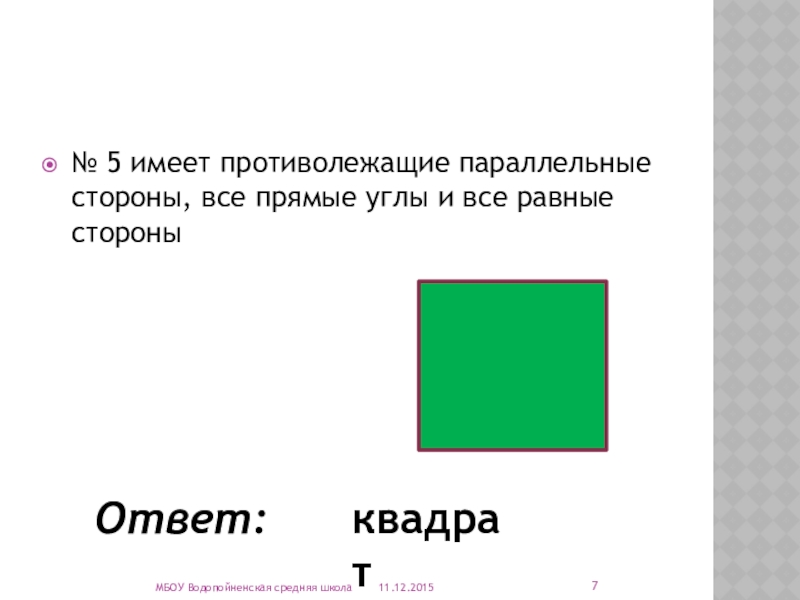
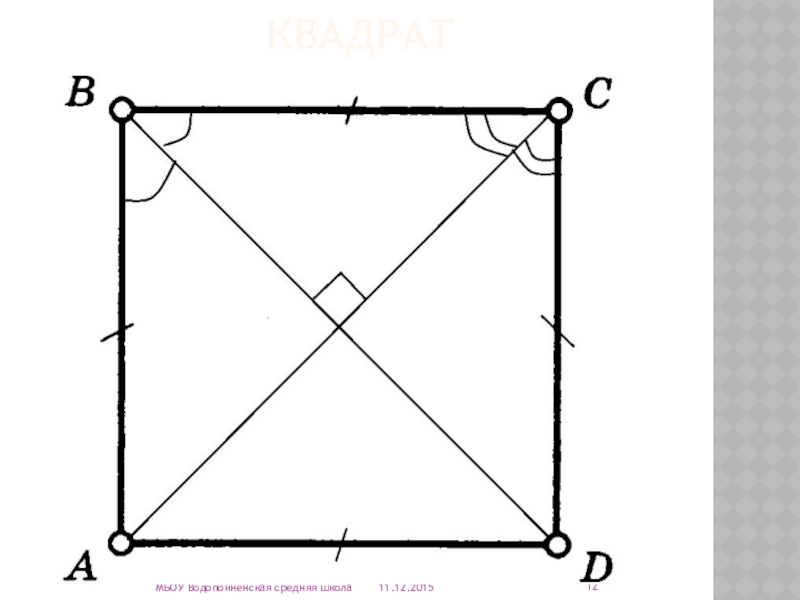
- 7. № 5 имеет противолежащие параллельные стороны, все прямые углы и все равные стороныМБОУ Водопойненская средняя школаОтвет:квадрат
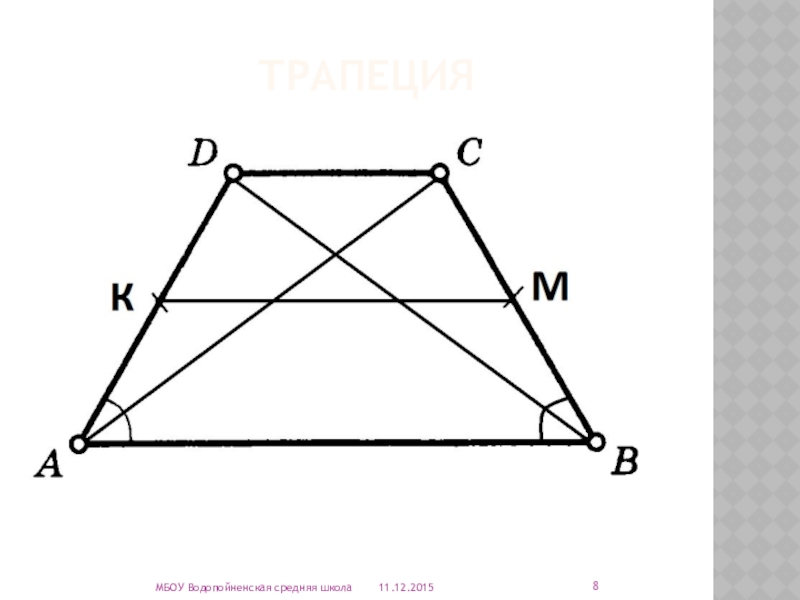
- 8. трапецияЕсли у трапеции две боковые стороны равны,
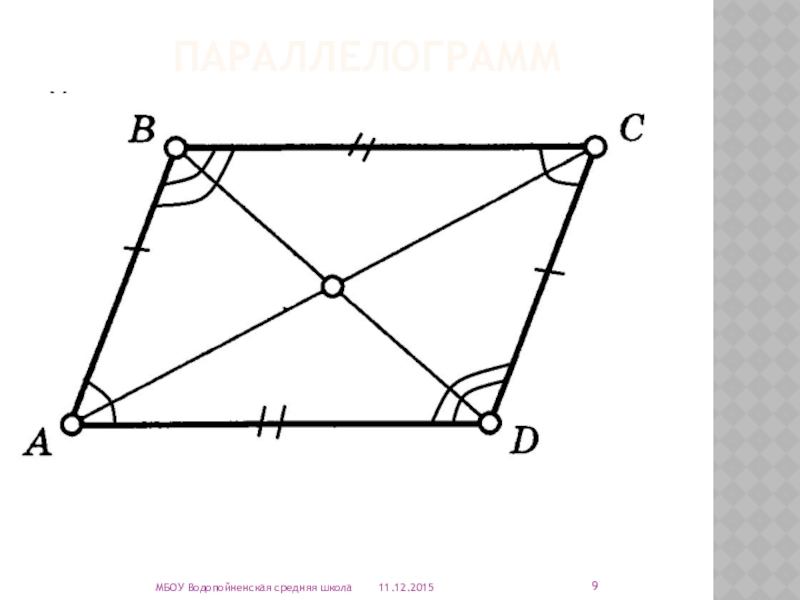
- 9. параллелограммУ параллелограмма диагонали пересекаются и точкой пересечения
- 10. прямоугольникДиагонали прямоугольника пересекаются и точкой пересечения делятся
- 11. ромбДиагонали ромба пересекаются и точкой пересечения делятся
- 12. квадратДиагонали квадрата пересекаются и делятся точкой пересечения
- 13. МБОУ Водопойненская средняя школа
- 14. Докажите, что если в параллелограмме все углы
- 15. Докажите, что четырехугольник, у которого все
- 16. Докажите, что если диагонали прямоугольника пересекаются
- 17. ФизкультминуткаМБОУ Водопойненская средняя школа
- 18. По рисунку докажите, что
- 19. МБОУ Водопойненская средняя школа
- 20. Домашнее заданиеСоставить отчетную таблицу (опорный конспект) по теме «Четырехугольники».МБОУ Водопойненская средняя школа
- 21. Спасибо за вниманиеМБОУ Водопойненская средняя школа
Слайд 1
Четырёхугольники
Выполнила учитель математики
МБОУ Водопойненская средняя школа
Апазова Л.Ж.
Слайд 2Цель: обобщить основные теоретические сведения о параллелограмме, прямоугольнике, ромбе, квадрате, трапеции,
МБОУ Водопойненская средняя школа
Слайд 3№ 1 только две противолежащие стороны параллельны.
МБОУ Водопойненская средняя школа
Ответ
трапеция.
Слайд 5прямоугольник
№ 3 противолежащие стороны параллельны и все углы прямые.
МБОУ Водопойненская средняя
Ответ:
Слайд 6№ 4 противолежащие стороны параллельны и все равны между собой.
МБОУ Водопойненская
Ответ:
ромб
Слайд 7№ 5 имеет противолежащие параллельные стороны, все прямые углы и все
МБОУ Водопойненская средняя школа
Ответ:
квадрат
Слайд 8трапеция
Если у трапеции две боковые стороны равны, она называется равнобокой.
У
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
МБОУ Водопойненская средняя школа
Слайд 9параллелограмм
У параллелограмма диагонали пересекаются и точкой пересечения делятся пополам.
Противолежащие стороны
Противолежащие углы параллелограмма равны.
Углы, прилежащие к одной стороне параллелограмма, дают в сумме 180°.
Диагональ параллелограмма делит его на два равных треугольника.
МБОУ Водопойненская средняя школа
Слайд 10прямоугольник
Диагонали прямоугольника пересекаются и точкой пересечения делятся пополам.
Диагонали прямоугольника равны.
МБОУ Водопойненская средняя школа
Слайд 11ромб
Диагонали ромба пересекаются и точкой пересечения делятся пополам.
Диагонали ромба являются
Диагонали ромба пересекаются под прямым углом.
Противолежащие углы ромба равны.
Сумма углов, прилежащих к одной стороне ромба, равна 180°.
МБОУ Водопойненская средняя школа
Слайд 12квадрат
Диагонали квадрата пересекаются и делятся точкой пересечения пополам.
Диагонали квадрата равны.
Диагонали квадрата пересекаются под прямым углом.
МБОУ Водопойненская средняя школа
Слайд 14Докажите, что если в параллелограмме все углы равны, то он является
Доказательство:
Поскольку данная фигура — параллелограмм, то сумма углов, прилежащих к одной из его сторон, равна 180°. По условию все углы равны. Таким образом, два угла, прилежащих к одной стороне параллелограмма, будут составлять по 90°, а так как противолежащие углы в параллелограмме равны, то и два других угла будут по 90°. Значит, данная фигура по определению — прямоугольник.
МБОУ Водопойненская средняя школа
Слайд 15Докажите, что четырехугольник,
у которого все стороны равны,
является ромбом.
Доказательство:
Рассмотрим
МБОУ Водопойненская средняя школа
Слайд 16Докажите, что если диагонали прямоугольника пересекаются под прямым углом, то он
Доказательство:
Пусть АВСВ — прямоугольник
АС ВD по условию, АС=ВD (свойство диагоналей прямоугольника), АО=СО=ВО=ОD (свойство диагоналей прямоугольника). Отсюда следует равенство прямоугольных треугольников: ∆АОВ=∆ВОС=∆СОD=∆АОD. Значит, АВ=ВС=СD=АD. Таким образом АВСD — прямоугольник , у которого все стороны равны. Значит, АВСD — квадрат, что и требовалось доказать.
МБОУ Водопойненская средняя школа
Слайд 18
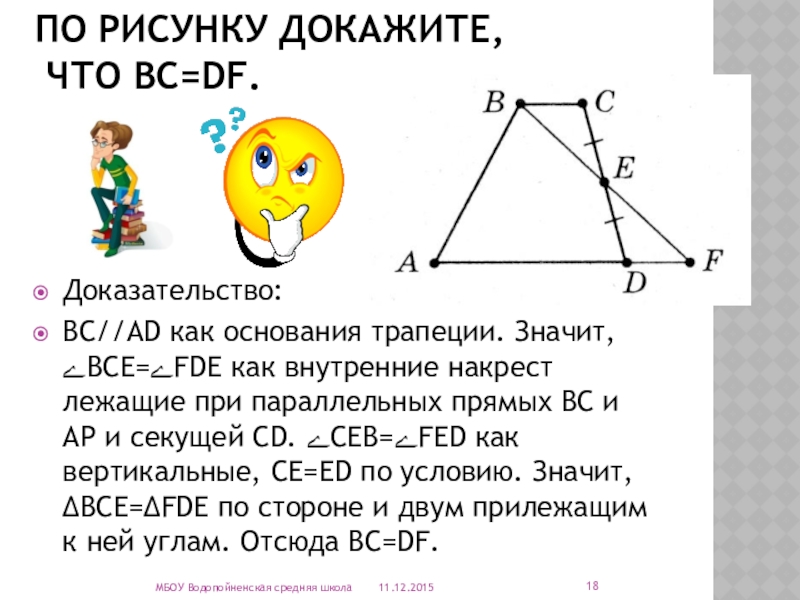
По рисунку докажите,
что ВС=DF.
Доказательство:
ВС//АD как основания трапеции. Значит, ےВСЕ=ےFDЕ как
МБОУ Водопойненская средняя школа