- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к проекту Теорема Пифагора в реальной жизни(10 класс)
Содержание
- 1. Презентация к проекту Теорема Пифагора в реальной жизни(10 класс)
- 2. Древнеиндийская задачаНад озером тихим С полфута размером
- 3. Исторические задачиЗадача индийского математика 12 века Бхаскары:«На
- 4. Слайд 4
- 5. ОБЛАСТИ ПРИМЕНЕНИЯСтроительствоАстрономияМобильная связь
- 6. Слайд 6
- 7. Если b обозначает ширину окна, то радиусы
- 8. Строительство крышиВ доме задумано построить двускатную крышу
- 9. МолниеотводИзвестно, что молниеотвод защищает от молнии все
- 10. АстрономияНа этом рисунке показаны точки A и
- 11. Мобильная связьКакую наибольшую высоту должна иметь антенна
- 12. Слайд 12
- 13. Пребудет вечной истина, как скороЕё познает слабый
- 14. Слайд 14
- 15. Слайд 15
- 16. СтроительствоОкнаКрышиМолниеотводы
- 17. Слайд 17
Древнеиндийская задачаНад озером тихим С полфута размером Он рос одиноко. И ветер порывом отнес его в сторону. Нет
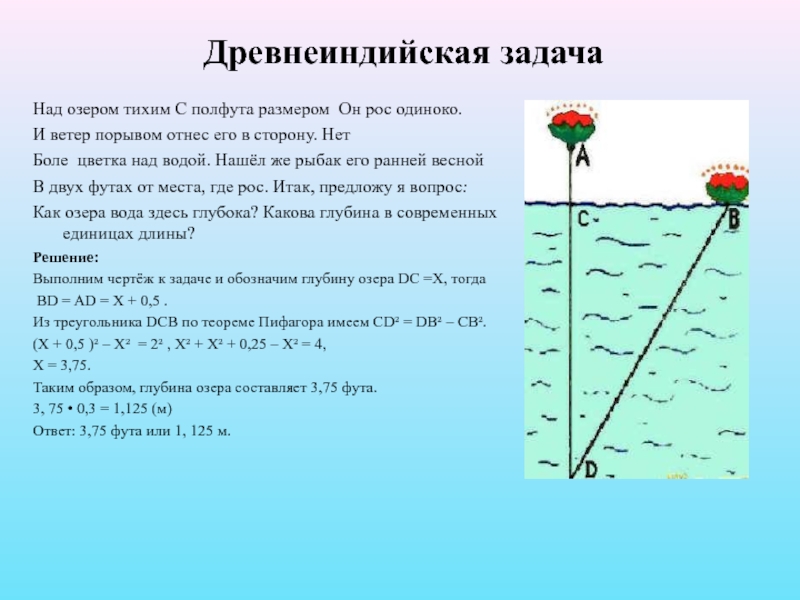
Слайд 2Древнеиндийская задача
Над озером тихим С полфута размером Он рос одиноко.
И
ветер порывом отнес его в сторону. Нет
Боле цветка над водой. Нашёл же рыбак его ранней весной
В двух футах от места, где рос. Итак, предложу я вопрос:
Как озера вода здесь глубока? Какова глубина в современных единицах длины?
Решение:
Выполним чертёж к задаче и обозначим глубину озера DС =Х, тогда
BD = AD = Х + 0,5 .
Из треугольника DCB по теореме Пифагора имеем CD² = DB² – CB².
(Х + 0,5 )² – Х² = 2² , Х² + Х² + 0,25 – Х² = 4,
Х = 3,75.
Таким образом, глубина озера составляет 3,75 фута.
3, 75 • 0,3 = 1,125 (м)
Ответ: 3,75 фута или 1, 125 м.
Боле цветка над водой. Нашёл же рыбак его ранней весной
В двух футах от места, где рос. Итак, предложу я вопрос:
Как озера вода здесь глубока? Какова глубина в современных единицах длины?
Решение:
Выполним чертёж к задаче и обозначим глубину озера DС =Х, тогда
BD = AD = Х + 0,5 .
Из треугольника DCB по теореме Пифагора имеем CD² = DB² – CB².
(Х + 0,5 )² – Х² = 2² , Х² + Х² + 0,25 – Х² = 4,
Х = 3,75.
Таким образом, глубина озера составляет 3,75 фута.
3, 75 • 0,3 = 1,125 (м)
Ответ: 3,75 фута или 1, 125 м.
Слайд 3Исторические задачи
Задача индийского математика 12 века Бхаскары:
«На берегу реки рос тополь
одинокий Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С течением реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
Решение: пусть СD – высота тополя,
DC=CB + BD, по теореме Пифагора имеем
АС² + СВ² = АВ²,
3² + 4² = 25, АВ = 5 футов. CD = 3+5 = 8(футов)
Ответ: 8 футов.
Бедный тополь упал. И угол прямой
С течением реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
Решение: пусть СD – высота тополя,
DC=CB + BD, по теореме Пифагора имеем
АС² + СВ² = АВ²,
3² + 4² = 25, АВ = 5 футов. CD = 3+5 = 8(футов)
Ответ: 8 футов.
Слайд 7Если b обозначает ширину окна, то радиусы полуокружностей будут равны R = b / 2
и r = b / 4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+p, один катет равен b/4, а другой b/2-p. По теореме Пифагора имеем:
(b/4+p) ²=( b/4) ²+( b/2-p) ²
или
b²/16+ bp/2+p²=b²/16+b²/4-bp+p²,
откуда
bp/2=b²/4-bp.
Разделив на b и приводя подобные члены, получим:
(3/2)p=b/4, p=b/6.
(b/4+p) ²=( b/4) ²+( b/2-p) ²
или
b²/16+ bp/2+p²=b²/16+b²/4-bp+p²,
откуда
bp/2=b²/4-bp.
Разделив на b и приводя подобные члены, получим:
(3/2)p=b/4, p=b/6.
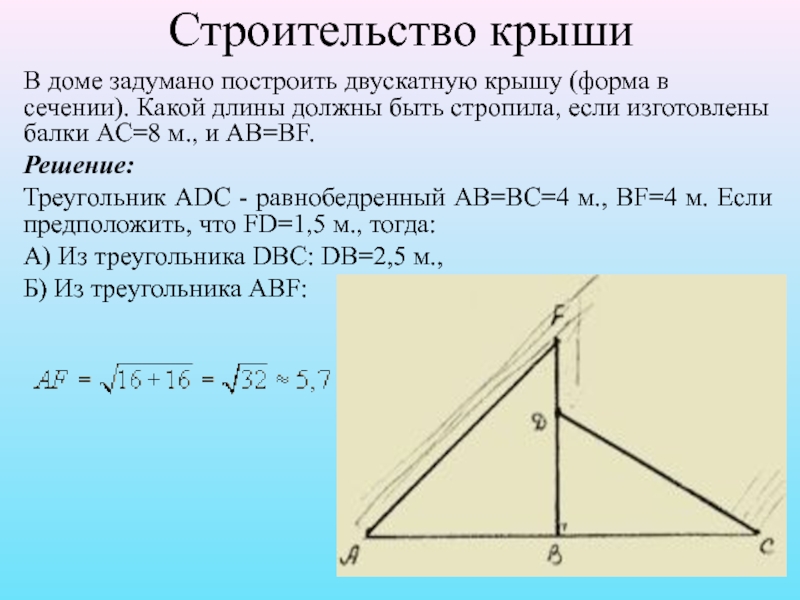
Слайд 8Строительство крыши
В доме задумано построить двускатную крышу (форма в сечении). Какой
длины должны быть стропила, если изготовлены балки AC=8 м., и AB=BF.
Решение:
Треугольник ADC - равнобедренный AB=BC=4 м., BF=4 м. Если предположить, что FD=1,5 м., тогда:
А) Из треугольника DBC: DB=2,5 м.,
Б) Из треугольника ABF:
Решение:
Треугольник ADC - равнобедренный AB=BC=4 м., BF=4 м. Если предположить, что FD=1,5 м., тогда:
А) Из треугольника DBC: DB=2,5 м.,
Б) Из треугольника ABF:
Слайд 9Молниеотвод
Известно, что молниеотвод защищает от молнии все предметы, расстояние которых от
его основания не превышает его удвоенной высоты. Необходимо определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.
Решение: По теореме Пифагора h2≥ a2+b2, значит h≥(a2+b2)1/2.
Решение: По теореме Пифагора h2≥ a2+b2, значит h≥(a2+b2)1/2.
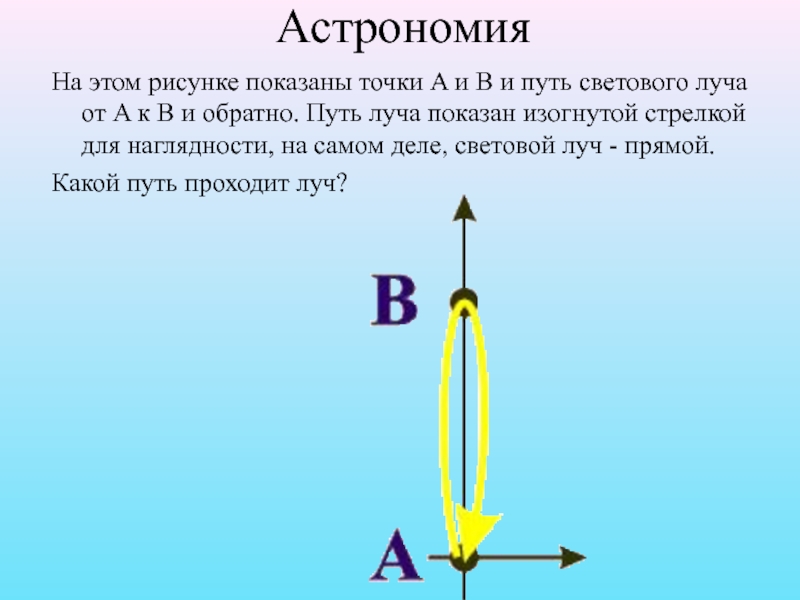
Слайд 10Астрономия
На этом рисунке показаны точки A и B и путь светового
луча от A к B и обратно. Путь луча показан изогнутой стрелкой для наглядности, на самом деле, световой луч - прямой.
Какой путь проходит луч?
Какой путь проходит луч?
Слайд 11Мобильная связь
Какую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу
можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.)
Решение: Пусть AB= x, BC=R=200 км, OC= r =6380 км.
OB=OA+AB OB=r + x.
Используя теорему
Пифагора, получим
ответ: 2,3 км.
Решение: Пусть AB= x, BC=R=200 км, OC= r =6380 км.
OB=OA+AB OB=r + x.
Используя теорему
Пифагора, получим
ответ: 2,3 км.
Слайд 13Пребудет вечной истина, как скоро
Её познает слабый человек!
И ныне теорема Пифагора
Верна,
как и в его далёкий век.
Слайд 17
Окна
В романской архитектуре часто встречается мотив, представленный на рисунке. Если b обозначает ширину окна, то радиусы полуокружностей будут равны R = b / 2 и r = b / 4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+p, один катет равен b/4, а другой b/2-p. По теореме Пифагора имеем:
(b/4+p) ²=( b/4) ²+( b/2-p) ²
или
b²/16+ bp/2+p²=b²/16+b²/4-bp+p²,
откуда
bp/2=b²/4-bp.
Разделив на b и приводя подобные члены, получим:
(3/2)p=b/4, p=b/6.
В романской архитектуре часто встречается мотив, представленный на рисунке. Если b обозначает ширину окна, то радиусы полуокружностей будут равны R = b / 2 и r = b / 4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+p, один катет равен b/4, а другой b/2-p. По теореме Пифагора имеем:
(b/4+p) ²=( b/4) ²+( b/2-p) ²
или
b²/16+ bp/2+p²=b²/16+b²/4-bp+p²,
откуда
bp/2=b²/4-bp.
Разделив на b и приводя подобные члены, получим:
(3/2)p=b/4, p=b/6.