- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Геометрия 9 класс Правильные многоугольники
Содержание
- 1. Презентация Геометрия 9 класс Правильные многоугольники
- 2. Домашнее задание
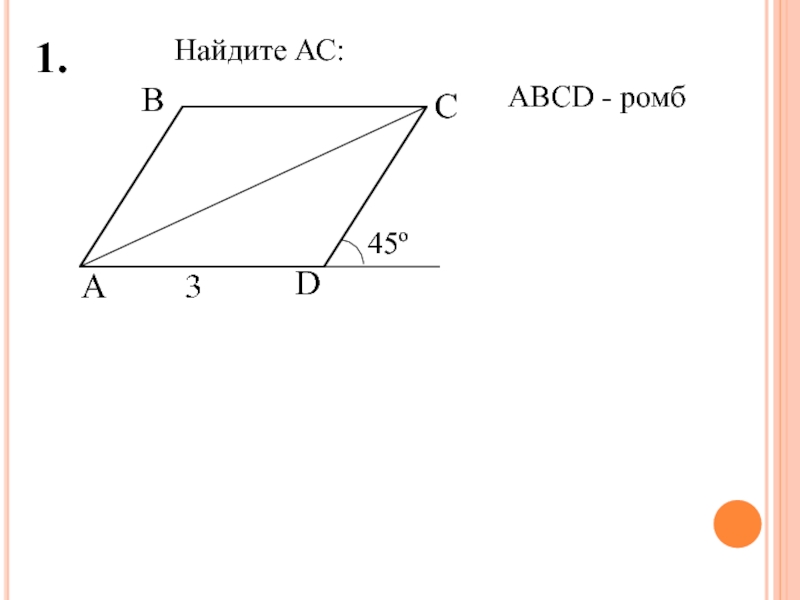
- 3. Найдите АС:ВСАD45ºАВСD - ромб1.
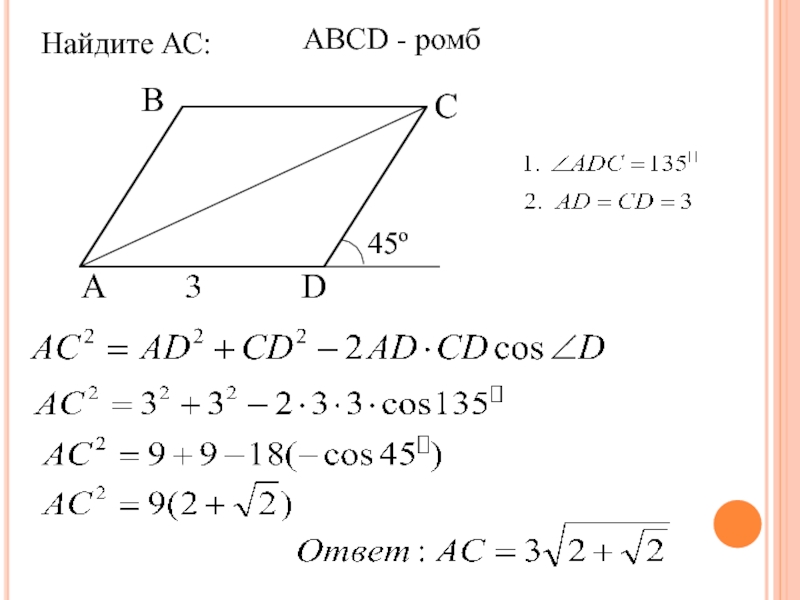
- 4. Найдите АС:ВСАD45ºАВСD - ромб
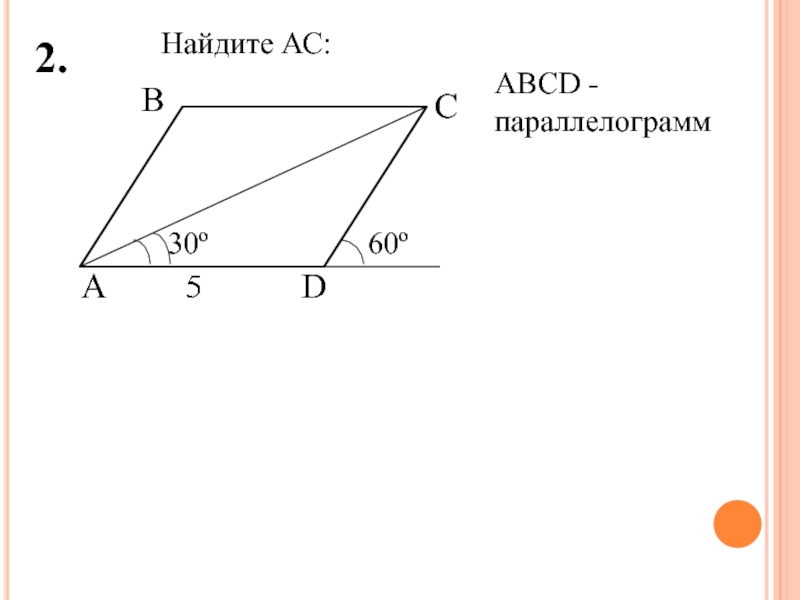
- 5. Найдите АС:ВСАD60ºАВСD - параллелограмм30º2.
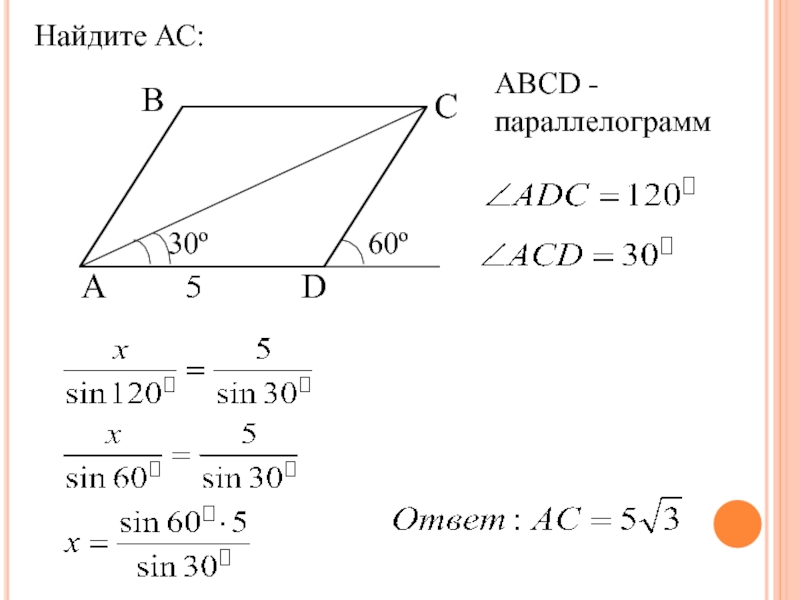
- 6. Найдите АС:ВСАD60ºАВСD - параллелограмм30º
- 7. Правильные многоугольники
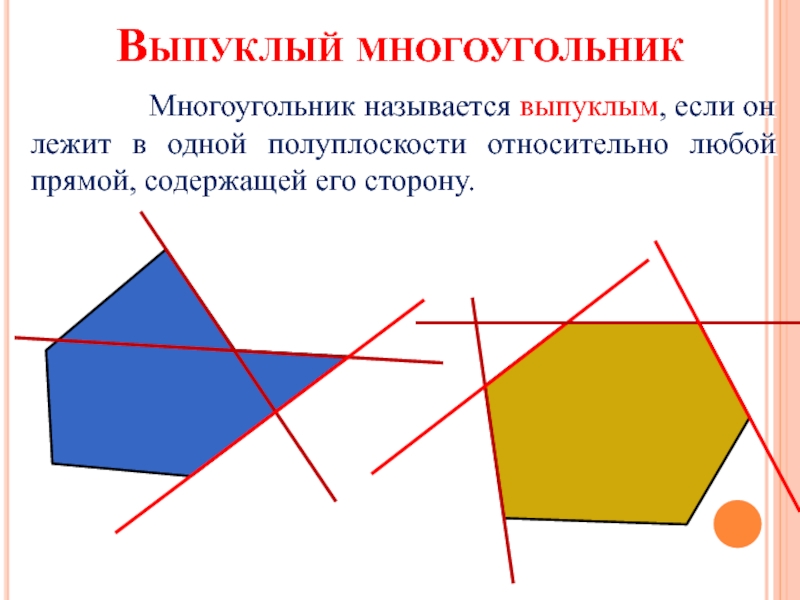
- 8. Выпуклый многоугольник
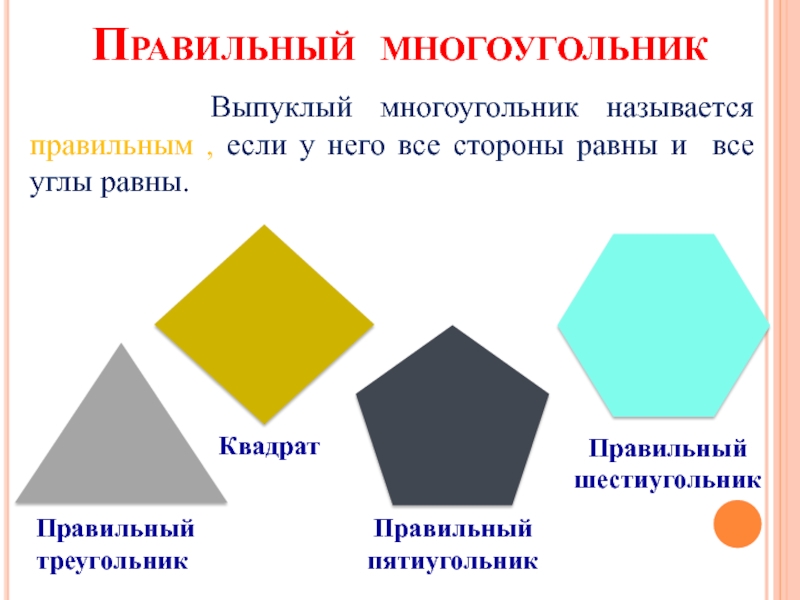
- 9. Правильный многоугольникПравильный треугольникКвадратПравильный пятиугольникПравильный шестиугольник
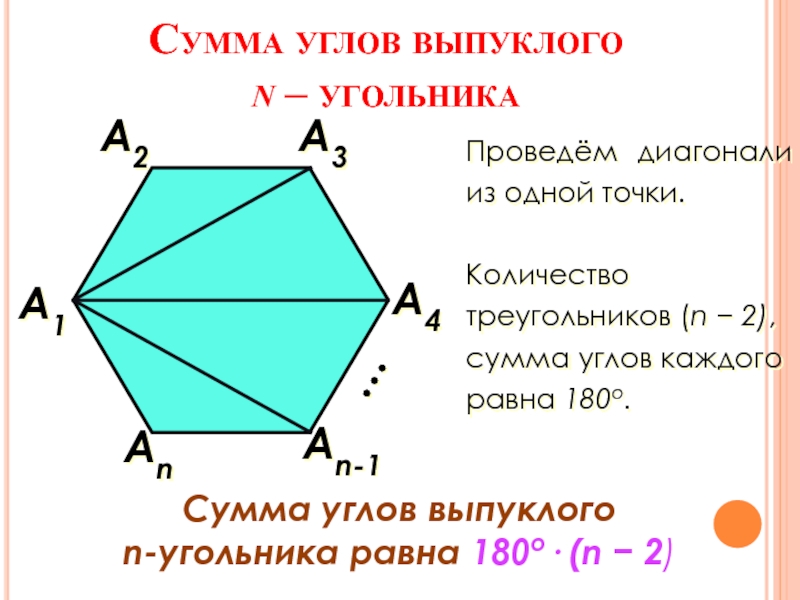
- 10. Сумма углов выпуклого n – угольника
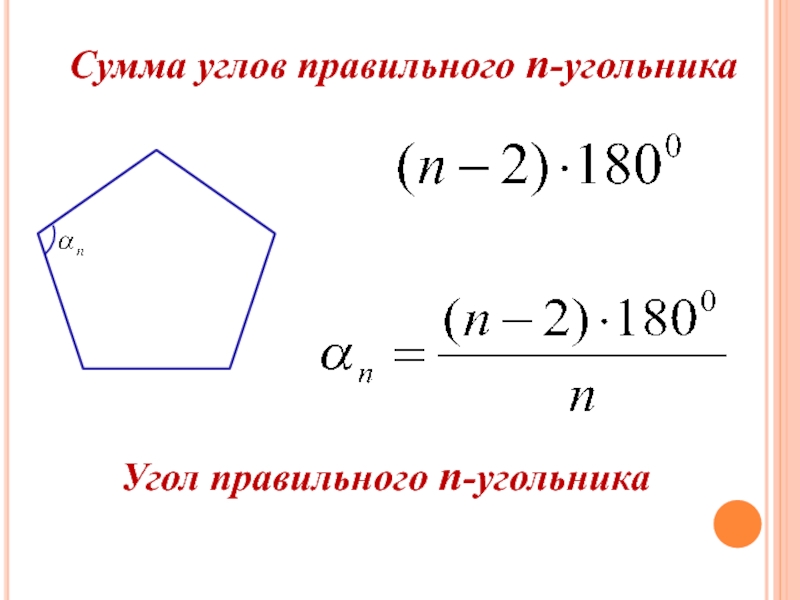
- 11. Сумма углов правильного n-угольникаУгол правильного n-угольника
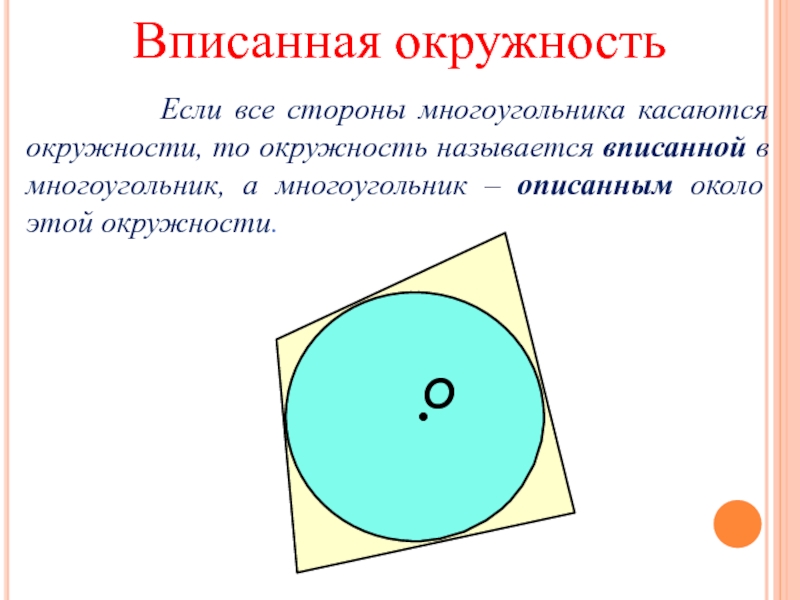
- 12. Вписанная окружность
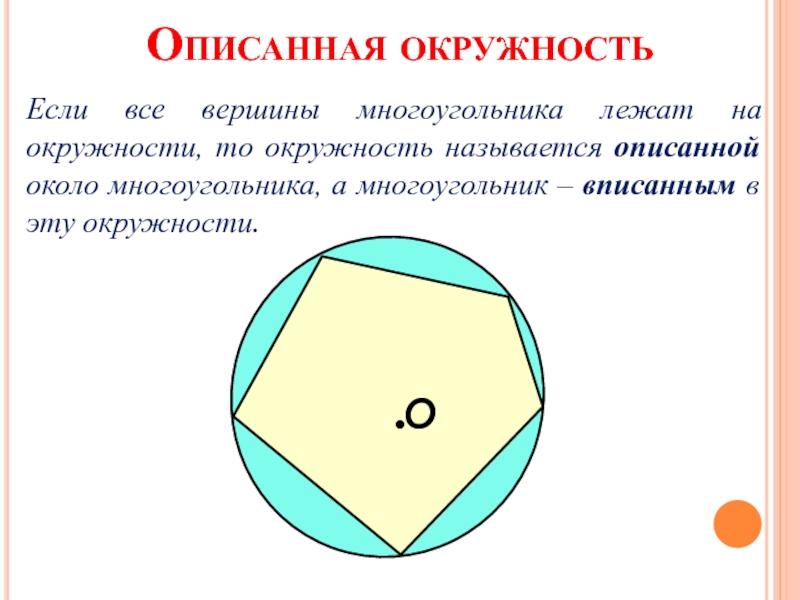
- 13. Описанная окружность Если все вершины многоугольника лежат
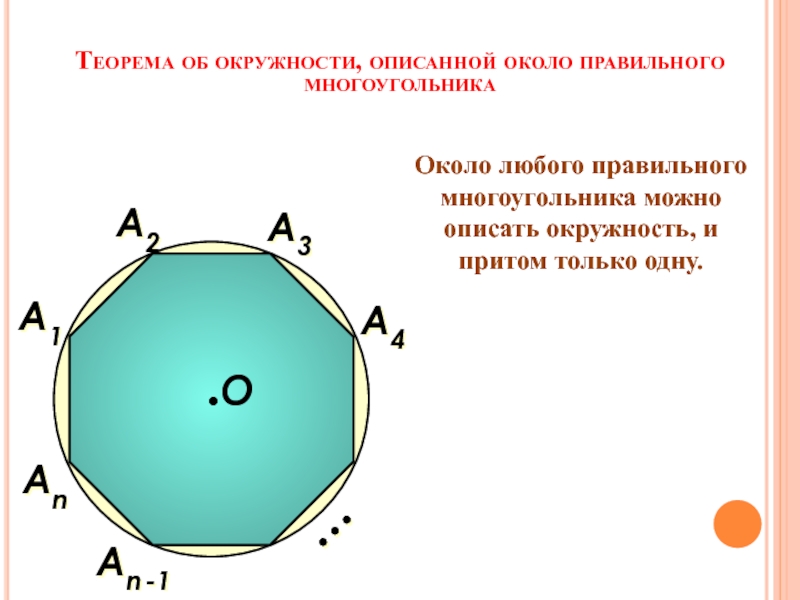
- 14. Теорема об окружности, описанной около правильного многоугольникаА1Аn
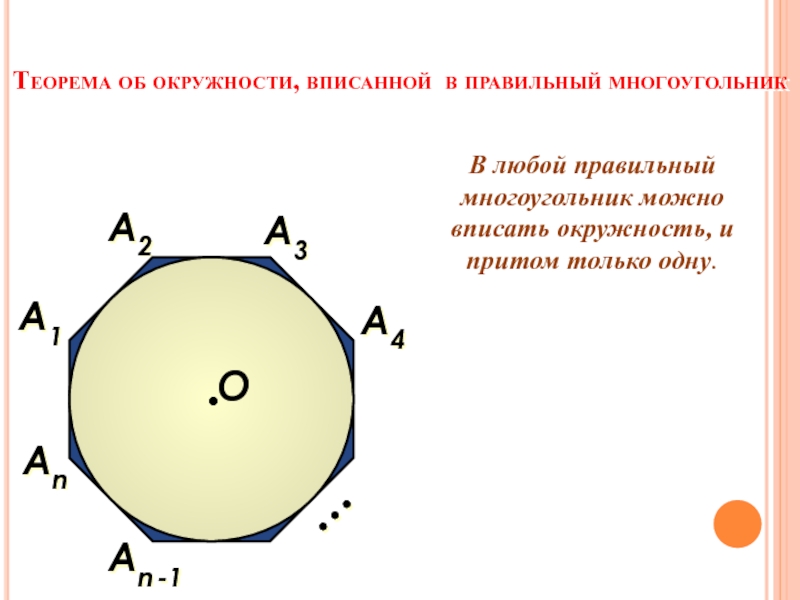
- 15. Теорема об окружности, вписанной в правильный многоугольникА2А1Аn
- 16. ОRrСледствие 2 Центр окружности описаннойоколо правильногомногоугольника, совпадает
- 17. Слайд 17
- 18. Построение правильного шестиугольника, сторона которого равна данному
- 19. Задача. Как, используя правильный шестиугольник построить правильный
- 20. Задача. Как, используя правильный шестиугольник построить правильный
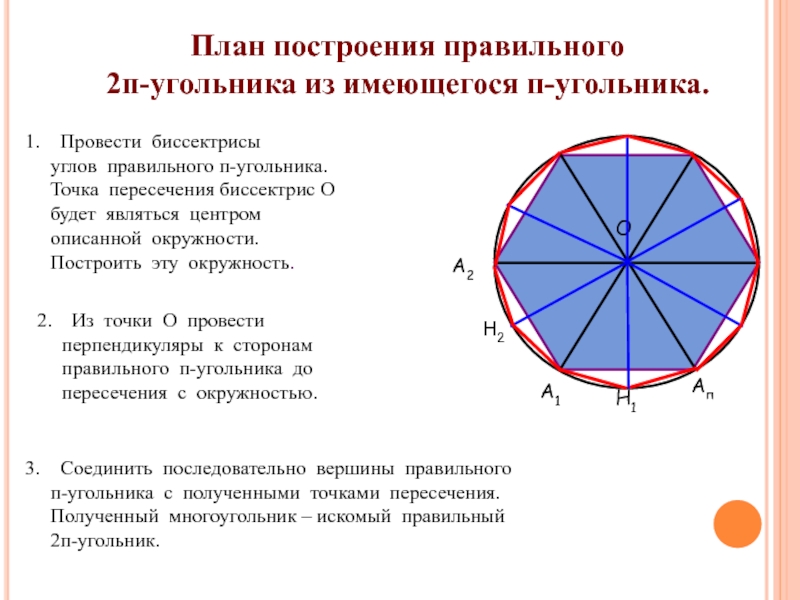
- 21. АпА1А2ОН1План построения правильного 2п-угольника из имеющегося п-угольника.Провести
- 22. Домашнее задание Радиус окружности, описанной около квадрата,
- 23. Слайд 23
- 24. Слайд 24
- 25. Радиус окружности, описанной около правильного шестиугольника, равен
Домашнее задание
Слайд 8Выпуклый многоугольник
Многоугольник называется
выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.
Слайд 9Правильный многоугольник
Правильный
треугольник
Квадрат
Правильный
пятиугольник
Правильный
шестиугольник
Выпуклый многоугольник называется
правильным , если у него все стороны равны и все углы равны.
Слайд 10Сумма углов выпуклого
n – угольника
А1
Аn
А4
А3
А2
Проведём диагонали из одной точки.
Количество
треугольников (n − 2), сумма углов каждого равна 180о.
Сумма углов выпуклого
n-угольника равна 180о· (n − 2)
Аn-1
…
Слайд 12Вписанная окружность
Если все стороны
многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.
О
Слайд 13Описанная окружность
Если все вершины многоугольника лежат на окружности, то окружность
называется описанной около многоугольника, а многоугольник – вписанным в эту окружности.
О
Слайд 14Теорема об окружности, описанной около правильного многоугольника
А1
Аn -1
А3
А2
Аn
…
А4
Около любого правильного многоугольника
можно описать окружность, и притом только одну.
О
Слайд 15Теорема об окружности, вписанной в правильный многоугольник
А2
А1
Аn -1
А3
Аn
…
А4
В любой правильный многоугольник
можно вписать окружность, и притом только одну.
О
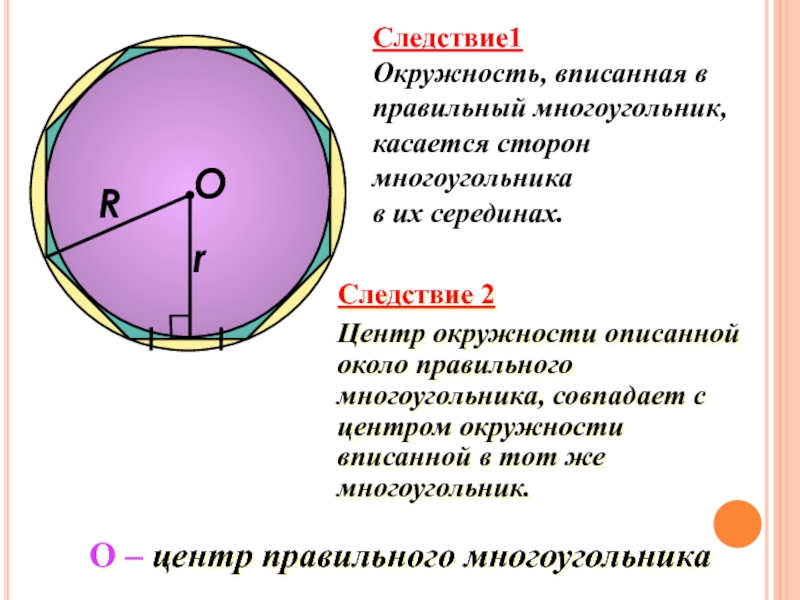
Слайд 16О
R
r
Следствие 2
Центр окружности описанной
около правильного
многоугольника, совпадает с центром окружности
вписанной в
тот же
многоугольник.
многоугольник.
Следствие1
Окружность, вписанная в правильный многоугольник,
касается сторон
многоугольника
в их серединах.
О – центр правильного многоугольника
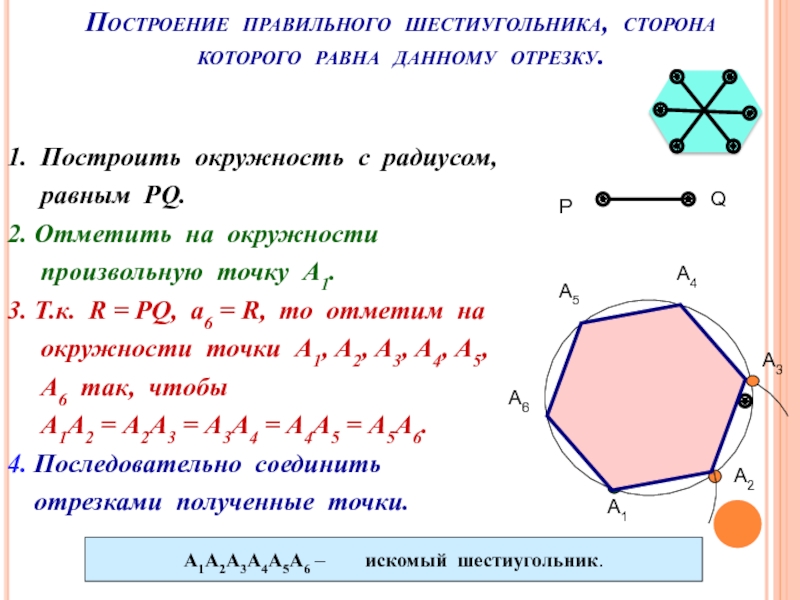
Слайд 18Построение правильного шестиугольника, сторона которого равна данному отрезку.
1. Построить окружность с
радиусом,
равным PQ.
2. Отметить на окружности
произвольную точку А1.
3. Т.к. R = PQ, а6 = R, то отметим на
окружности точки А1, А2, А3, А4, А5,
А6 так, чтобы
А1А2 = А2А3 = А3А4 = А4А5 = А5А6.
4. Последовательно соединить
отрезками полученные точки.
равным PQ.
2. Отметить на окружности
произвольную точку А1.
3. Т.к. R = PQ, а6 = R, то отметим на
окружности точки А1, А2, А3, А4, А5,
А6 так, чтобы
А1А2 = А2А3 = А3А4 = А4А5 = А5А6.
4. Последовательно соединить
отрезками полученные точки.
P
Q
А1
А2
А3
А1А2А3А4А5А6 – искомый шестиугольник.
А4
А5
А6
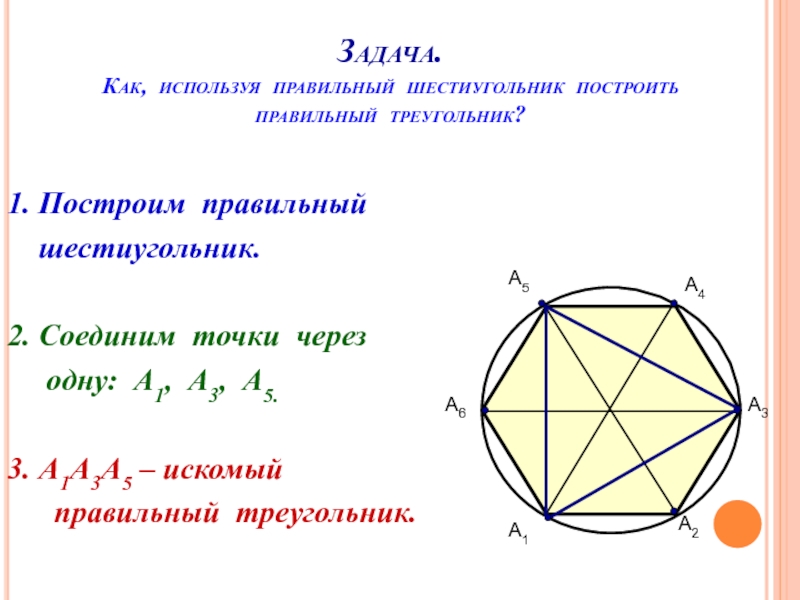
Слайд 19Задача.
Как, используя правильный шестиугольник построить правильный треугольник?
А1
А2
А3
А4
А5
А6
1. Построим правильный
шестиугольник.
2. Соединим точки через
одну: А1, А3, А5.
3. А1А3А5 – искомый
правильный треугольник.
2. Соединим точки через
одну: А1, А3, А5.
3. А1А3А5 – искомый
правильный треугольник.
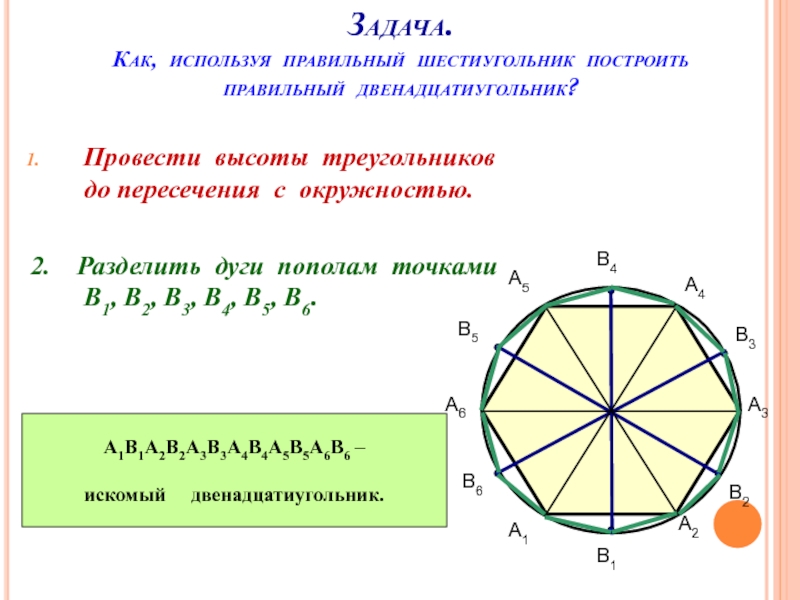
Слайд 20Задача.
Как, используя правильный шестиугольник построить правильный двенадцатиугольник?
Провести высоты треугольников до пересечения
с окружностью.
2. Разделить дуги пополам точками В1, В2, В3, В4, В5, В6.
2. Разделить дуги пополам точками В1, В2, В3, В4, В5, В6.
А1
А2
А3
А4
А5
А6
В1
В4
В2
В5
В3
В6
А1В1А2В2А3В3А4В4А5В5А6В6 –
искомый двенадцатиугольник.
Слайд 21Ап
А1
А2
О
Н1
План построения правильного
2п-угольника из имеющегося п-угольника.
Провести биссектрисы
углов правильного
п-угольника.
Точка пересечения биссектрис О
будет являться центром
описанной окружности.
Построить эту окружность.
Точка пересечения биссектрис О
будет являться центром
описанной окружности.
Построить эту окружность.
Н2
Из точки О провести
перпендикуляры к сторонам
правильного п-угольника до
пересечения с окружностью.
Соединить последовательно вершины правильного
п-угольника с полученными точками пересечения.
Полученный многоугольник – искомый правильный
2п-угольник.
Слайд 22Домашнее задание
Радиус окружности, описанной около квадрата,
равен 4√3 см. Найдите сторону квадрата и радиус
вписанной в него окружности.
2. Радиус окружности, вписанной в правильный
шестиугольник, равен 4√3 см. Найдите сторону
шестиугольника и радиус описанной около него
окружности.
Найдите углы правильного n- угольника, если:
а) n=3; б) n=5; в) n=10; г) n=18.
4. Сколько сторон имеет правильный многоугольник, если каждый его угол равен: а)60о; б) 135о; в) 150о.
вписанной в него окружности.
2. Радиус окружности, вписанной в правильный
шестиугольник, равен 4√3 см. Найдите сторону
шестиугольника и радиус описанной около него
окружности.
Найдите углы правильного n- угольника, если:
а) n=3; б) n=5; в) n=10; г) n=18.
4. Сколько сторон имеет правильный многоугольник, если каждый его угол равен: а)60о; б) 135о; в) 150о.
Слайд 25Радиус окружности, описанной около правильного шестиугольника, равен 5 √3 см. Найдите
сторону шестиугольника, радиус окружности, вписанной в шестиугольник и его площадь.
