- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад для урока геометрии Свойство углов, образованных двумя параллельными прямыми и секущей
Содержание
- 1. Презентация для урока геометрии Свойство углов, образованных двумя параллельными прямыми и секущей
- 2. Евклид (III в. до н.э.)Аксиома параллельных прямых:через
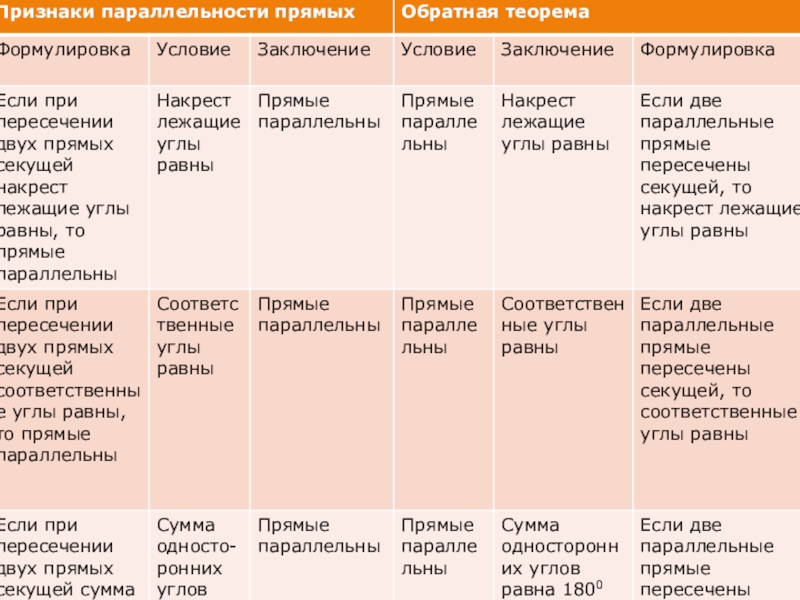
- 3. Свойство углов, образованных двумя параллельными прямыми и секущей
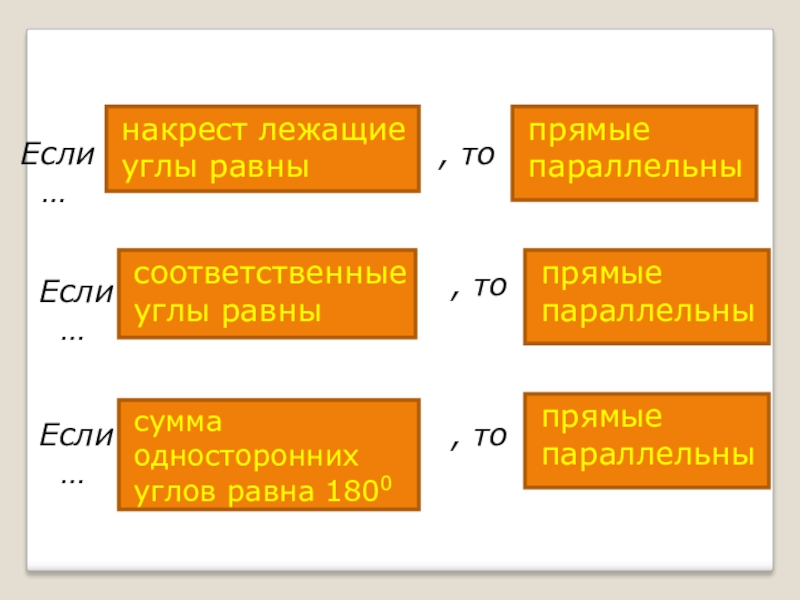
- 4. Высказывания, обратные даннымЕсли, тоЕсли, тоЕсли, то
- 5. Если …, тоЕсли …, тоЕсли …, то
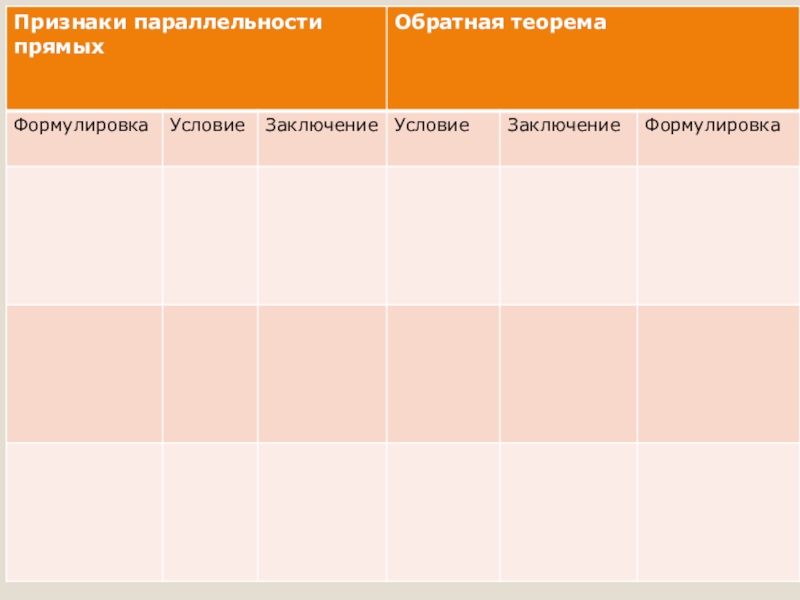
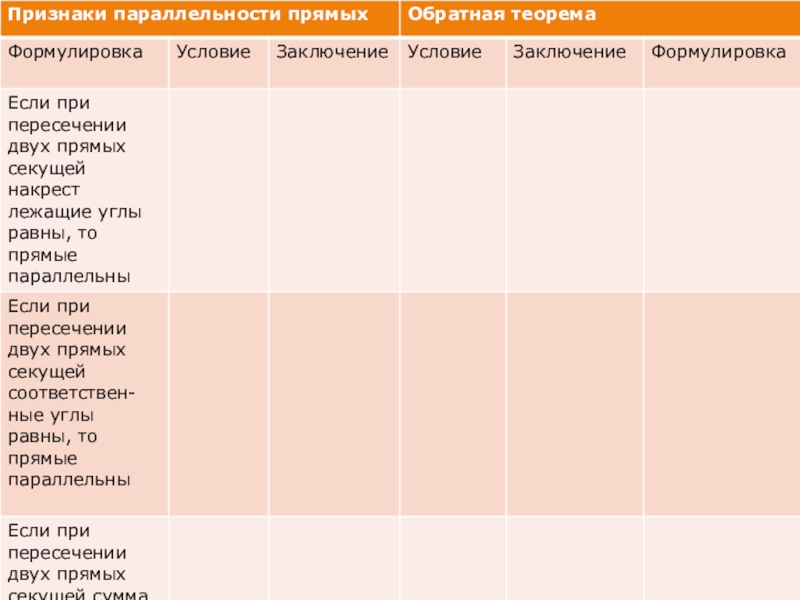
- 6. Слайд 6
- 7. Слайд 7
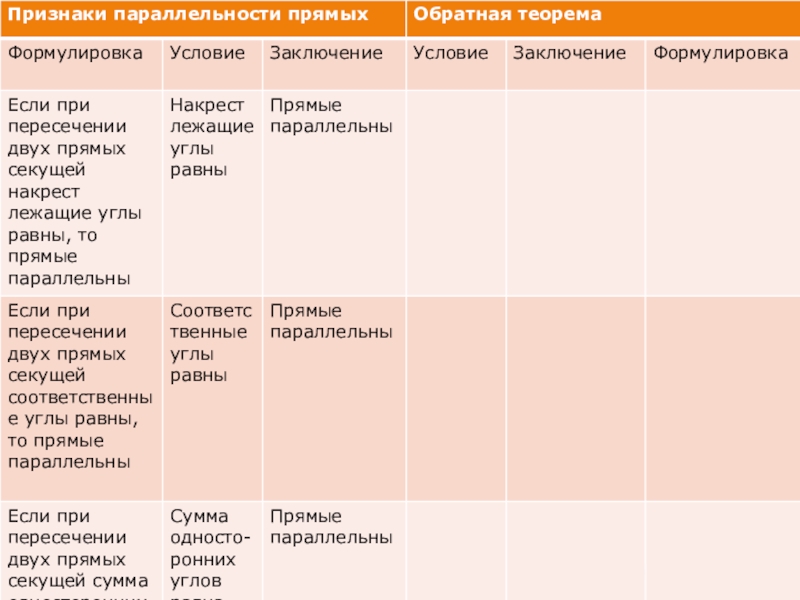
- 8. Слайд 8
- 9. Слайд 9
- 10. Метод доказательства теоремы – от противногоВрач после
- 11. Ревизор получил задание: выяснить есть ли в
- 12. Метод доказательства теоремы – от противного
- 13. Если две параллельные прямые пересечены секущей, то
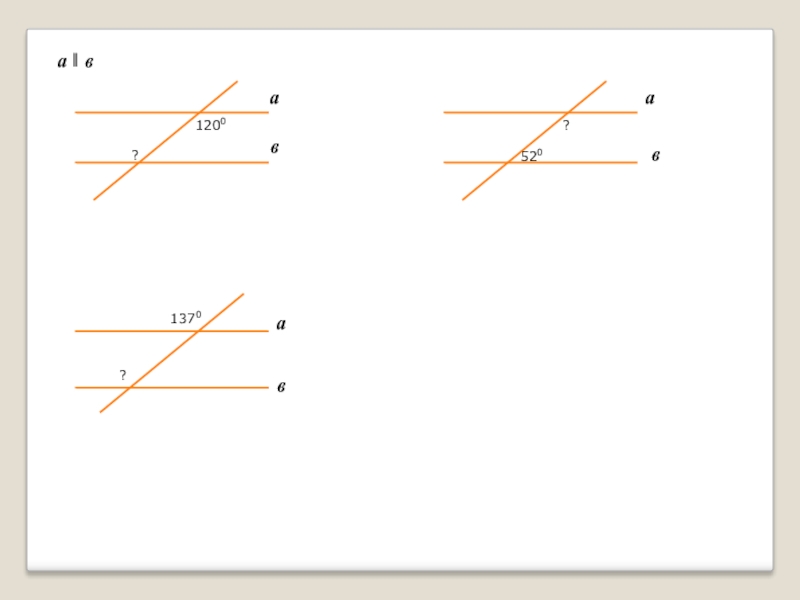
- 14. а ‖ вав1200?ав520?ав1370?
- 15. Домашнее задание:Знать свойства углов и их доказательство, записать доказательство второго и третьего свойства в тетрадь.
Евклид (III в. до н.э.)Аксиома параллельных прямых:через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной .
Слайд 2Евклид (III в. до н.э.)
Аксиома параллельных прямых:
через точку, не лежащую на
данной прямой, проходит только одна прямая, параллельная данной .
Слайд 10Метод доказательства теоремы –
от противного
Врач после осмотра больного ребенка доказывает родителям,
почему у него не аппендицит.
Предположим, что у ребенка аппендицит.
Из этого следует, что живот должен болеть с правой стороны.
Но живот болит не с правой стороны.
Значит, у ребенка не аппендицит.
Слайд 11Ревизор получил задание: выяснить есть ли в данном колхозе гусеничный трактор.
Председатель колхоза рассуждал так:
Предположим, что трактор есть.
Из этого следует, что должны быть следы гусениц.
Но их нет.
Значит в колхозе нет гусеничного трактора
Слайд 13Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны
а
в
с
d
1
2
3
Дано:
Доказать:
а ‖ в
∠1 =∠2
Доказательство методом от противного:
1.Предположим …
2.Из этого следует, что существует другой ∠3, равный ∠1.
3. ∠1 и ∠3 - …
На основании признака параллельности прямых прямые d и в …
Это противоречит аксиоме параллельных прямых, так как …
4.Значит предположение неверно, и ∠1 …∠2.
А
В
Слайд 15Домашнее задание:
Знать свойства углов и их доказательство, записать доказательство второго и
третьего свойства в тетрадь.
