практике
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Преобразование фигур (11 класс)
Содержание
- 1. Преобразование фигур (11 класс)
- 2. Существуют следующие преобразования плоскости ДвижениеПодобиеНазад
- 3. ДвижениеДвижение это преобразование плоскости, сохраняющее расстояние между
- 4. Симметрия относительно точки:Преобразование фигуры F в фигуру
- 5. Симметрия относительно точки:Если преобразование симметрии переводит фигуру
- 6. Симметрия относительно прямой:Преобразованием симметрии относительно прямой l,
- 7. Поворот:Параллельным переносом на вектор a называется отображение
- 8. Параллельный перенос:Преобразование плоскости, при котором все точки
- 9. Подобие:Преобразованием подобия называется преобразование, при котором расстояние
- 10. Гомотетия:Гомотетией с центром O и коэффициентом k ≠ 0
- 11. Движение в пространстве
- 12. ДвижениеДвижение – преобразование фигур, при котором сохраняются
- 13. Осевая симметрияОсевой симметрией с осью a называется
- 14. Центральная симметрияЦентральной симметрией относительно точки O называется такое
- 15. ПоворотПоворотом фигуры F вокруг центра O на
- 16. Зеркальная симметрияЗеркальной симметрией называется преобразование пространства относительно плоскости, совпадающее со своим обратным.
- 17. Параллельный переносПараллельным переносом называется движение, при котором
- 18. Композиции движенийКомпозиция – результат последовательного выполнения двух движений.Осевая симметрияПараллельный перенос
- 19. Подобие Преобразование подобия в пространстве определяется так
- 20. Свойства подобия:
- 21. ГомотетияПреобразование гомотетии в пространстве переводит любую плоскость,
- 22. Движение в природе, архитектуре, искусстве.
Существуют следующие преобразования плоскости ДвижениеПодобиеНазад
Слайд 1Симметрия в пространстве
Симметрия относительно точки, прямой, плоскости;
Симметрия в природе и на
Слайд 3Движение
Движение это преобразование плоскости, сохраняющее расстояние между точками. Существует 4 вида
движений.
Симметрия относительно точки;
Симметрия относительно прямой;
Поворот;
Параллельный перенос.
Симметрия относительно точки;
Симметрия относительно прямой;
Поворот;
Параллельный перенос.
Назад
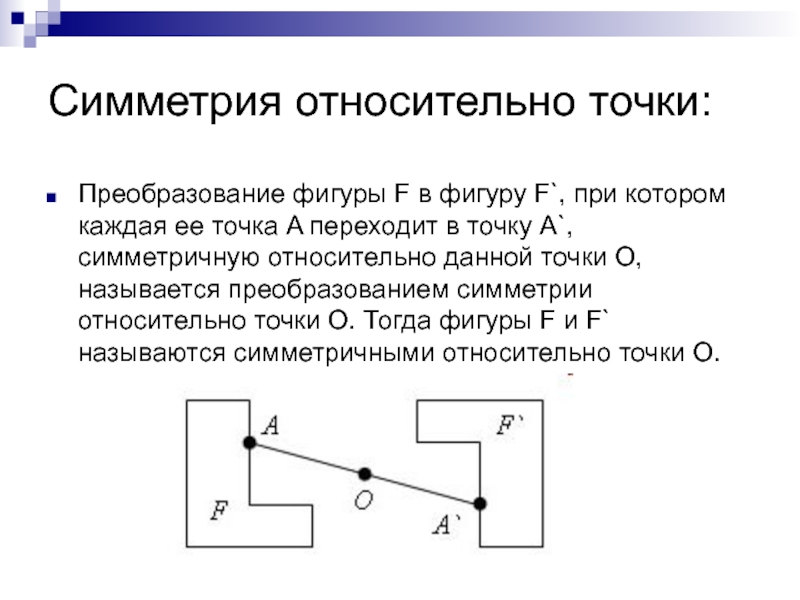
Слайд 4Симметрия относительно точки:
Преобразование фигуры F в фигуру F`, при котором каждая
ее точка A переходит в точку A`, симметричную относительно данной точки O, называется преобразованием симметрии относительно точки O. Тогда фигуры F и F` называются симметричными относительно точки O.
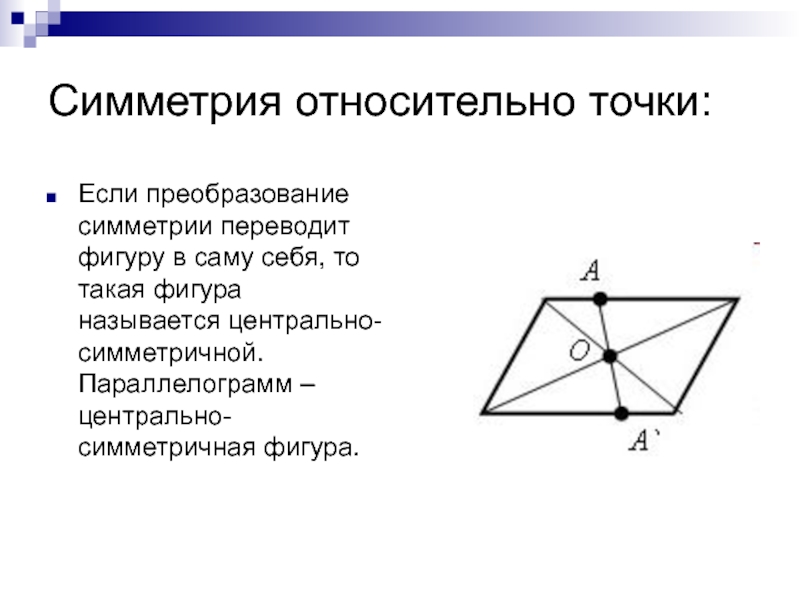
Слайд 5Симметрия относительно точки:
Если преобразование симметрии переводит фигуру в саму себя, то
такая фигура называется центрально-симметричной. Параллелограмм – центрально-симметричная фигура.
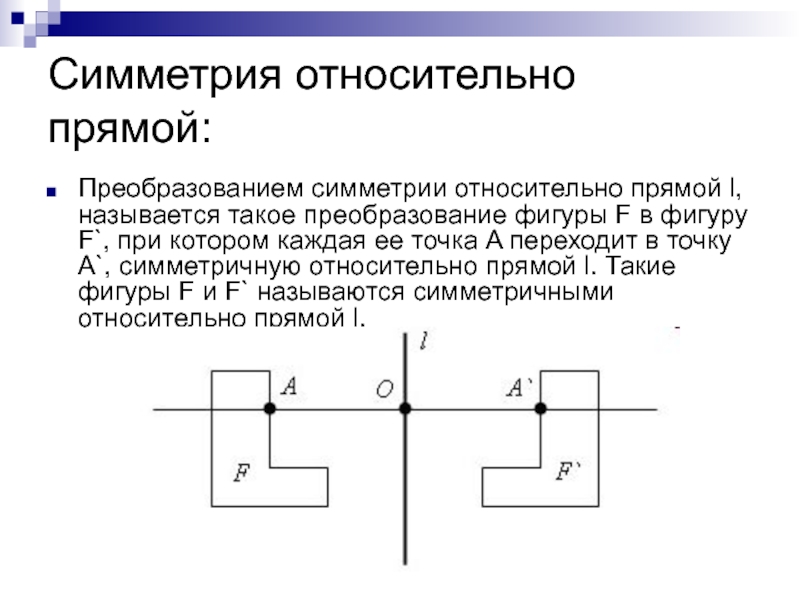
Слайд 6Симметрия относительно прямой:
Преобразованием симметрии относительно прямой l, называется такое преобразование фигуры
F в фигуру F`, при котором каждая ее точка A переходит в точку A`, симметричную относительно прямой l. Такие фигуры F и F` называются симметричными относительно прямой l.
Слайд 7Поворот:
Параллельным переносом на вектор a называется отображение плоскости на себя, при
котором каждая точка X переходит в точку X1
Слайд 8Параллельный перенос:
Преобразование плоскости, при котором все точки смещаются на одно и
то же расстояние, т.е. длины всех отрезков AA', где A' – образ точки A, равны и все лучи AA' сонаправлены.
Слайд 9Подобие:
Преобразованием подобия называется преобразование, при котором расстояние между любыми двумя точками
изменяется в одно и то же число раз.
Слайд 10Гомотетия:
Гомотетией с центром O и коэффициентом k ≠ 0 называется преобразование, при котором
каждой точке А ставится в соответствие точка А' так, что ОА' =k ОА
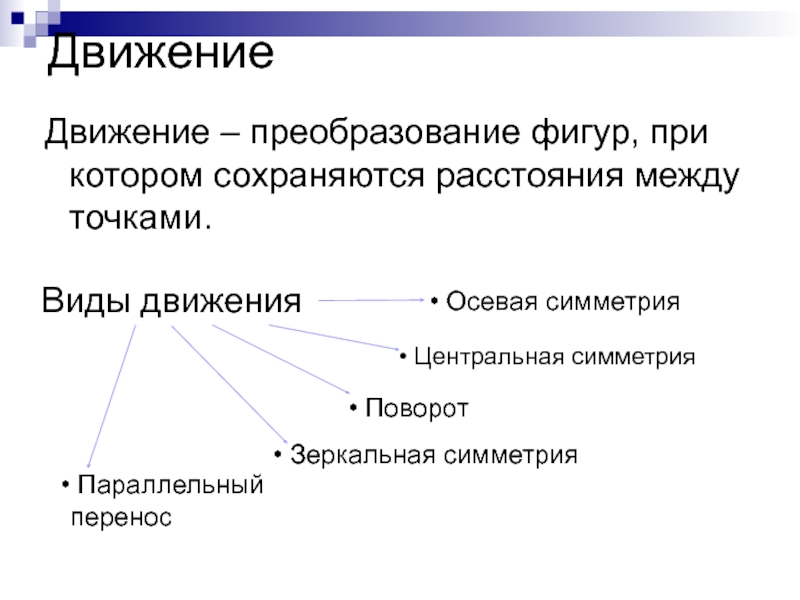
Слайд 12Движение
Движение – преобразование фигур, при котором сохраняются расстояния между точками.
Виды движения
Осевая симметрия
Поворот
Зеркальная симметрия
Центральная симметрия
Параллельный перенос
Слайд 13Осевая симметрия
Осевой симметрией с осью a называется такое преобразование фигуры F,
при котором каждой точке данной фигуры сопоставляется точка, симметричная ей относительно прямой a.
F
a
Слайд 14Центральная симметрия
Центральной симметрией относительно точки O называется такое преобразование фигуры F, при
котором каждой ее точке X сопоставляется точка симметрич-ная относительно точки O.
O
F
Слайд 15Поворот
Поворотом фигуры F вокруг центра O на данный угол φ (0° ≤ φ ≤ 180°) в
данном направлении называется такое ее преобразование, при котором каждой точке X F сопоставляется точка X ʹ так, что OX=OX ʹ
F
ф
O
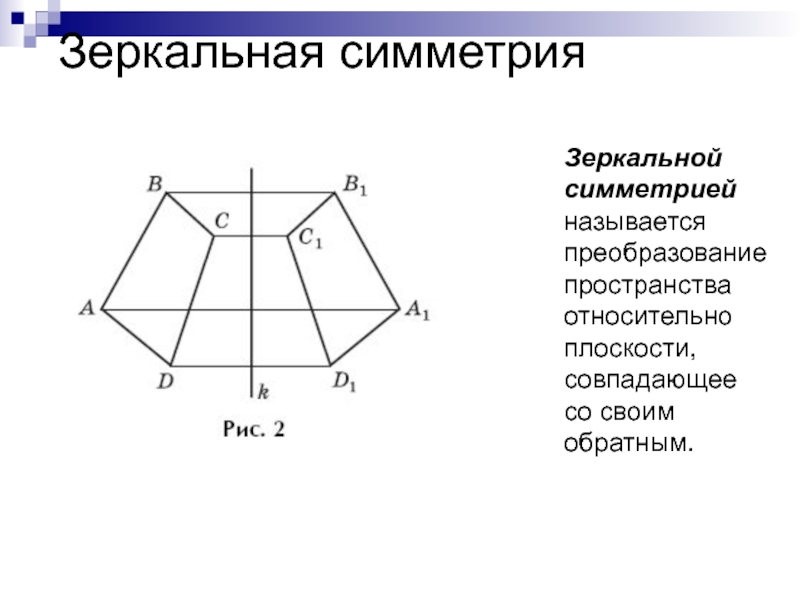
Слайд 16Зеркальная симметрия
Зеркальной симметрией называется преобразование пространства относительно плоскости, совпадающее со своим
обратным.
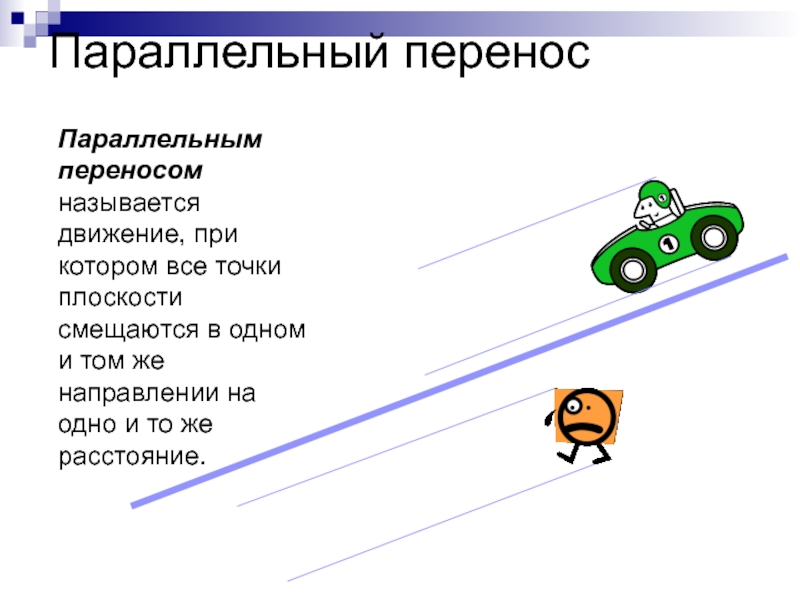
Слайд 17Параллельный перенос
Параллельным переносом называется движение, при котором все точки плоскости смещаются
в одном и том же направлении на одно и то же расстояние.
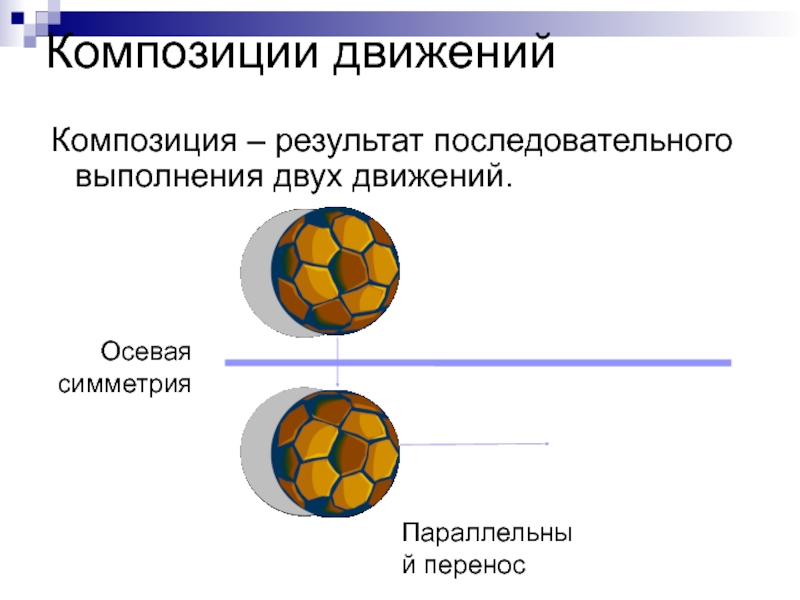
Слайд 18Композиции движений
Композиция – результат последовательного выполнения двух движений.
Осевая симметрия
Параллельный перенос
Слайд 19Подобие
Преобразование подобия в пространстве определяется так же, как и на
плоскости, т.к. при этом преобразовании расстояния между точками изменяются в одно и то же число раз.
Слайд 20 Свойства подобия:
1. Подобие переводит прямые в прямые, полупрямые – в полупрямые, отрезки – в отрезки.
2. Подобие сохраняет углы между полупрямыми
3. Подобие переводит плоскости в плоскости.
2. Подобие сохраняет углы между полупрямыми
3. Подобие переводит плоскости в плоскости.
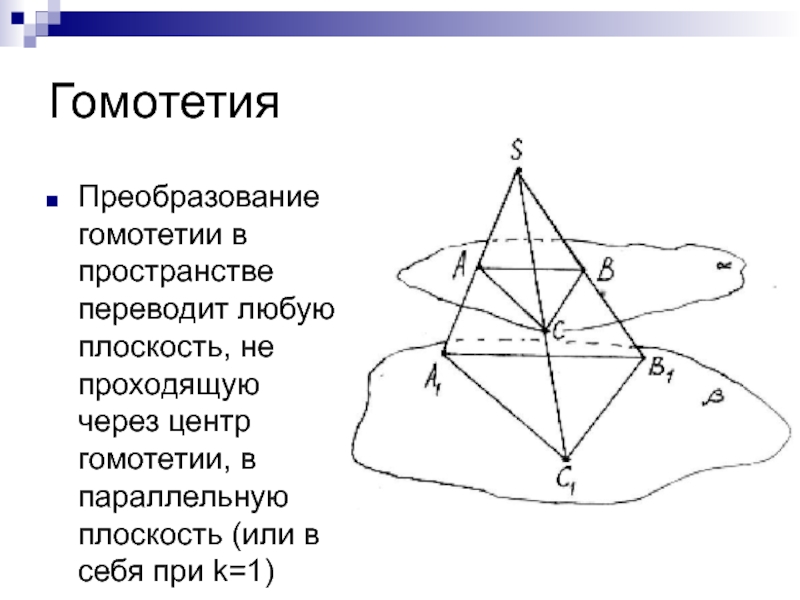
Слайд 21Гомотетия
Преобразование гомотетии в пространстве переводит любую плоскость, не проходящую через центр
гомотетии, в параллельную плоскость (или в себя при k=1)