Наталья Дмитриевна
г. Магнитогорск
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Площади плоских фигур (8 класс)
Содержание
- 1. Площади плоских фигур (8 класс)
- 2. 1 задание.
- 3. Задача: Сад имеет форму прямоугольника: длина составляет 580
- 4. Решение: 1. Рассчитаем площадь сада.S =
- 5. 2 задание.
- 6. Старая стена х 100 –
- 7. Слайд 7
- 8. 3 задание.
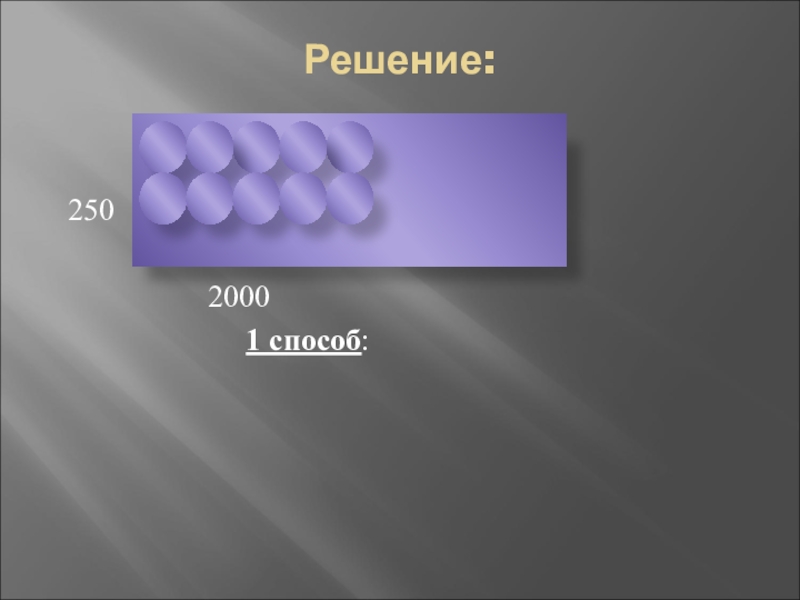
- 9. Решение: 250 2000
- 10. При данном раскрое, шайбы
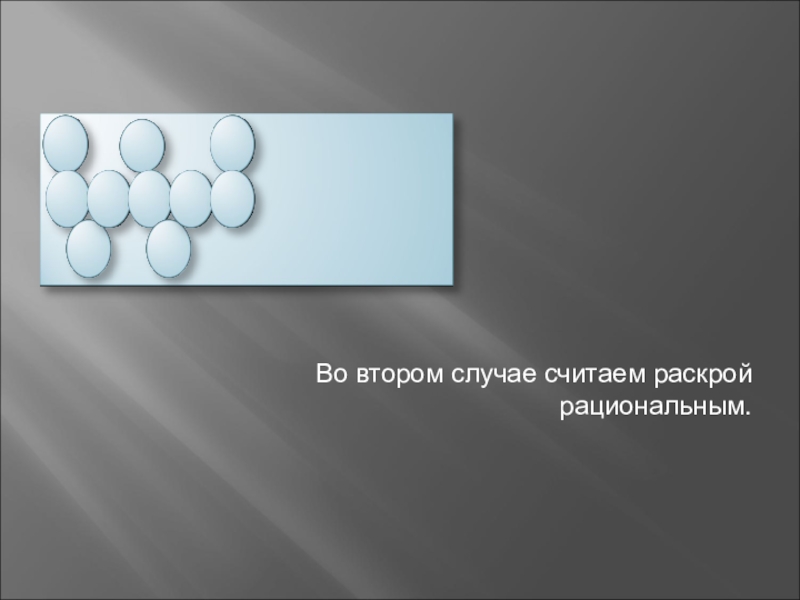
- 11. Во втором случае считаем раскрой рациональным.
- 12. Найдем, какова площадь отходов?Sполосы = 250 *
- 13. 4 задание.
- 14. Решение. 10210 см – на боковины и днища
- 15. Рассматривая второй способ изготовления ящиков, когда боковинами
- 16. Т. к. высота трапеции 10 см, то
- 17. 5 задание.
- 18. Решение: Для того, чтобы решить эту задачу,
- 19. 2.) NP || BD
1 задание. В жизнь села все более полно входит арендный подряд. Представьте, что к вам обратилась группа семей, которые решили объединиться и взять у совхоза в аренду яблоневый сад. Совхоз выделяет
Слайд 21 задание.
В жизнь села все
более полно входит арендный подряд. Представьте, что к вам обратилась группа семей, которые решили объединиться и взять у совхоза в аренду яблоневый сад. Совхоз выделяет участок размерами 580 х 376м.
Известно, что средний урожай яблок с 1-ой яблони составляет 56 кг, средняя цена реализации одной тонны яблок – 60 000 рублей, затраты на выращивание урожая яблок составляют 12 600 рублей в год на одну тонну собранных яблок и арендная плата будет равна 4 882 672 рубля в год. Что вы им посоветуете? Насколько будет выгодным это дело? (дополнительные сведения для решения задачи: на каждую яблоню в среднем приходится по 16 м2 земли.)
Известно, что средний урожай яблок с 1-ой яблони составляет 56 кг, средняя цена реализации одной тонны яблок – 60 000 рублей, затраты на выращивание урожая яблок составляют 12 600 рублей в год на одну тонну собранных яблок и арендная плата будет равна 4 882 672 рубля в год. Что вы им посоветуете? Насколько будет выгодным это дело? (дополнительные сведения для решения задачи: на каждую яблоню в среднем приходится по 16 м2 земли.)
Слайд 3Задача:
Сад имеет форму прямоугольника: длина составляет 580 м, а ширина -
376 м.
Подсчитать, какую выручку даст сад после
продажи яблок. Выгодно ли будет взять его в
аренду сельчанам?
Подсчитать, какую выручку даст сад после
продажи яблок. Выгодно ли будет взять его в
аренду сельчанам?
Слайд 4 Решение:
1. Рассчитаем площадь сада.
S = 580*376= 218 080 (м2) =
21,8 (га).
2. Сколько яблонь размещается на данном участке?
n = 218 080: 16 = 13 630 (штук корней)
3. Сколько тонн яблок можно получить?
13 630*56 = 763 280 (кг) = 763 280 (кг).
4. Сколько можно выручить денег?
763 280*60 000 = 45 796 800 (руб.)
5. Каковы затраты на выращивание яблок?
12 600* 763,28 = 9 617 328 (руб.)
6. Каковы затраты с учетом арендной платы?
9 617 328+ 4 882 672 = 14 500 000 (руб.)
7. Какова прибыль?
45 796 800 –14 500 000 = 31 296 800 (руб.)
Прибыль составила более 50 % - это выгодный показатель в условиях применения арендного подряда, даже в капиталистических странах у предпринимателей.
2. Сколько яблонь размещается на данном участке?
n = 218 080: 16 = 13 630 (штук корней)
3. Сколько тонн яблок можно получить?
13 630*56 = 763 280 (кг) = 763 280 (кг).
4. Сколько можно выручить денег?
763 280*60 000 = 45 796 800 (руб.)
5. Каковы затраты на выращивание яблок?
12 600* 763,28 = 9 617 328 (руб.)
6. Каковы затраты с учетом арендной платы?
9 617 328+ 4 882 672 = 14 500 000 (руб.)
7. Какова прибыль?
45 796 800 –14 500 000 = 31 296 800 (руб.)
Прибыль составила более 50 % - это выгодный показатель в условиях применения арендного подряда, даже в капиталистических странах у предпринимателей.
Слайд 52 задание.
Чтобы иметь возможность регулярных
занятий учащихся в спортивных секциях во внеурочное время, шефы решили пристроить к существующей стене школы дополнительный спортзал.
После предварительных подсчетов, оказалось, что кирпича у них хватит только на 100 м стены (по периметру 3-х новых стен). Естественное желание: зал должен быть как можно большим по площади. Что вы им посоветуете? Какие размеры пристройки выбрать?
После предварительных подсчетов, оказалось, что кирпича у них хватит только на 100 м стены (по периметру 3-х новых стен). Естественное желание: зал должен быть как можно большим по площади. Что вы им посоветуете? Какие размеры пристройки выбрать?
Слайд 6 Старая стена
х
100 – 2х
Пусть х
м – длина одной новой стены пристройки, противоположная стена тоже будет х м, тогда другая, 3 –я будет равна
(100 – 2х) м.
Найдем S зала = х (100 – 2х) м 2.
(100 – 2х) м.
Найдем S зала = х (100 – 2х) м 2.
Слайд 7
Выясним, при каком х выражение принимает свое наибольшее значение. Для этого выделим полный квадрат
x (100 – 2х) = - 2х 2 + 100х = - 2(х 2 – 50х) =
= - 2 (х 2 – 2*х*25 + 625 – 625) = - 2 (х – 25) 2 + +1250 = 1250 – 2 * (х – 25) 2.
Так как из 1250 вычитается неотрицательное число, то наибольшее значение выражение х (100 – 2х), при х = 25, равно 1250. Вывод: размеры зала должны быть 25 х 50 м, т.е. площадь зала будет 1250 м 2.
x (100 – 2х) = - 2х 2 + 100х = - 2(х 2 – 50х) =
= - 2 (х 2 – 2*х*25 + 625 – 625) = - 2 (х – 25) 2 + +1250 = 1250 – 2 * (х – 25) 2.
Так как из 1250 вычитается неотрицательное число, то наибольшее значение выражение х (100 – 2х), при х = 25, равно 1250. Вывод: размеры зала должны быть 25 х 50 м, т.е. площадь зала будет 1250 м 2.
Слайд 83 задание.
Вы работаете слесарем –
инструментальщиком. Вам поручено изготовить запорные шайбы диаметром 100 мм из стальной полосы 250 х 2000 мм. Предложите наиболее рациональный раскрой полосы, определите наибольшее количество шайб, которое можно изготовить, сколько процентов металла уйдет в отходы?
Задача: Раскроить полосу, показать 2 способа, рациональный, нерациональный.
Задача: Раскроить полосу, показать 2 способа, рациональный, нерациональный.
Слайд 10
При данном раскрое, шайбы располагаем одна
под
другой. Решение в данном случае сводится к
нахождению расстояния между центрами шайб.
1 ряд: 2000 : 100 = 20 (штук)
20 * 2 = 40 (шайб)
нахождению расстояния между центрами шайб.
1 ряд: 2000 : 100 = 20 (штук)
20 * 2 = 40 (шайб)
Слайд 12Найдем, какова площадь отходов?
Sполосы = 250 * 2 000 = 500 000
(мм2)
Sшайб = Пч2 * 46 = 3, 14 * 2 500 * 46 = 361 100 (мм2)
Sотходов = 500 000 – 361 100 = 138 900 (мм2)
138 900:500 000 * 100 % = 27, 78 (%) – составляет площадь отходов.
Sшайб = Пч2 * 46 = 3, 14 * 2 500 * 46 = 361 100 (мм2)
Sотходов = 500 000 – 361 100 = 138 900 (мм2)
138 900:500 000 * 100 % = 27, 78 (%) – составляет площадь отходов.
Слайд 134 задание.
Всем школам нашего района поручено
вырастить по 200 – 250 штук корней герани для посадки на площади перед администрацией города.
Для выращивания герани необходимо изготовить ящики. В мастерской имеется лист фанеры размером 220 * 80 см. Для удобства размещения на стеллажах предлагается изготовить 2 вида ящиков, но с одинаковым посадочным полем. Первый вид ящиков изготавливается из боковин прямоугольной формы размером 30 * 10 см. Второй вид ящиков с боковиной в форме равнобокой трапеции с основаниями 30 и 10 см, острым углом в 45о . Как вы считаете, при каком виде ящиков, используя один и тот же лист фанеры, можно изготовить их максимальное количество? (Они представляют, работают с самой площадью, представляют визуально, познают площадь, как объективную реальность).
Для выращивания герани необходимо изготовить ящики. В мастерской имеется лист фанеры размером 220 * 80 см. Для удобства размещения на стеллажах предлагается изготовить 2 вида ящиков, но с одинаковым посадочным полем. Первый вид ящиков изготавливается из боковин прямоугольной формы размером 30 * 10 см. Второй вид ящиков с боковиной в форме равнобокой трапеции с основаниями 30 и 10 см, острым углом в 45о . Как вы считаете, при каком виде ящиков, используя один и тот же лист фанеры, можно изготовить их максимальное количество? (Они представляют, работают с самой площадью, представляют визуально, познают площадь, как объективную реальность).
Слайд 15Рассматривая второй способ изготовления ящиков, когда боковинами будут служить равнобокие трапеции,
но для того, чтобы сделать разметку боковин в форме трапеции, необходимо выполнить предварительно и расчеты по нахождению высоты.
1. Проведем ВК и СМ – высоты.
2. ΔАВК = ΔСМД (прямоугольные
а) АВ = СД – по условию,
т.к. трапеция равнобокая)
б) ВК = СМ – по построению, как высоты,
или расстояния между двумя сторонами.
3. ВС = КМ (по определению прямоугольника)
4 АК = МД, то АК + МД = 30 – 10 = 20, АК = МД = 10 см.
5. ΔАВК и ΔСМД – равнобедренные, т.к. А = Д = 45о, АВК = МСД = 45о, значит АК = ВК = 10 см.
1. Проведем ВК и СМ – высоты.
2. ΔАВК = ΔСМД (прямоугольные
а) АВ = СД – по условию,
т.к. трапеция равнобокая)
б) ВК = СМ – по построению, как высоты,
или расстояния между двумя сторонами.
3. ВС = КМ (по определению прямоугольника)
4 АК = МД, то АК + МД = 30 – 10 = 20, АК = МД = 10 см.
5. ΔАВК и ΔСМД – равнобедренные, т.к. А = Д = 45о, АВК = МСД = 45о, значит АК = ВК = 10 см.
Слайд 16Т. к. высота трапеции 10 см, то в одном ряду трапеция
укладывать 10 раз (попеременно приставляем к меньшему основанию большее, 45о). Всего в 7 рядах – 70 трапеций, остается полоса 10 х 80, но в ней тоже можно разместить 3 трапеции, получим 73 трапеции. Последний ряд оставим на днища, они будут 10 х 10 см.
73:4 = 18ящиков (1 трапеция – лишняя)
22 днища, берем 18, остается 4 днища 10 х 10, это минимальные отходы.
73:4 = 18ящиков (1 трапеция – лишняя)
22 днища, берем 18, остается 4 днища 10 х 10, это минимальные отходы.
Слайд 175 задание.
Представьте, что вы работаете
в проектной организации. На одной из площадей города начато сооружение фонтана. По проекту, фонтан имеет форму квадрата, в вершины которого подведены трубы для подачи воды. Строители, осуществив прокладку труб, приостановили работу на объекте. Когда решили продолжить сооружение фонтана, то оказалось, что по старому проекту он не будет соответствовать общему архитектурному ансамблю площади. Необходимо вдвое увеличить площадь фонтана, но в целях экономии затрат оставить неизменной подводку воды. Как бы вы это сделали?
.
.
Слайд 18Решение:
Для того, чтобы решить эту задачу, необходим чертеж.
1. Выполним доп. построение
(построим 2 квадрат)
2. Докажем, что второй четырехугольник будет квадратом.
3. Найдем площадь.
1.) MN || AC MN ┴ BD
QP || AC QP ┴ BD
.
2. Докажем, что второй четырехугольник будет квадратом.
3. Найдем площадь.
1.) MN || AC MN ┴ BD
QP || AC QP ┴ BD
.
Слайд 19 2.) NP || BD
MN ┴ AC
MQ || BD MQ ┴ AC
MN ┴ MQ
MN ┴ NP
Рассмотрим АСД (прямоугольник)
СД = АД = х SАВСД = х2
по th Пифагора АС = 2х2 = х 2
MN = AC = х 2 SMNPK = (х 2)2 = 2х2
Таким образом, S фонтана увеличена в 2 раза, из свойств квадрата и путем построения.
MQ || BD MQ ┴ AC
MN ┴ MQ
MN ┴ NP
Рассмотрим АСД (прямоугольник)
СД = АД = х SАВСД = х2
по th Пифагора АС = 2х2 = х 2
MN = AC = х 2 SMNPK = (х 2)2 = 2х2
Таким образом, S фонтана увеличена в 2 раза, из свойств квадрата и путем построения.