- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Открытый урок геометрии в 7 классе по теме Равнобедренный треугольник
Содержание
- 1. Открытый урок геометрии в 7 классе по теме Равнобедренный треугольник
- 2. Девиз нашего урока : «Есть в математике
- 3. «Установка» : «Развивать и тренировать своё геометрическое
- 4. О ожидающееспокойноеприподнятое
- 5. Треугольник – самая простая замкнутаягеометрическая фигура,
- 6. Из дошедших до нас сочинений Евклида наиболее
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
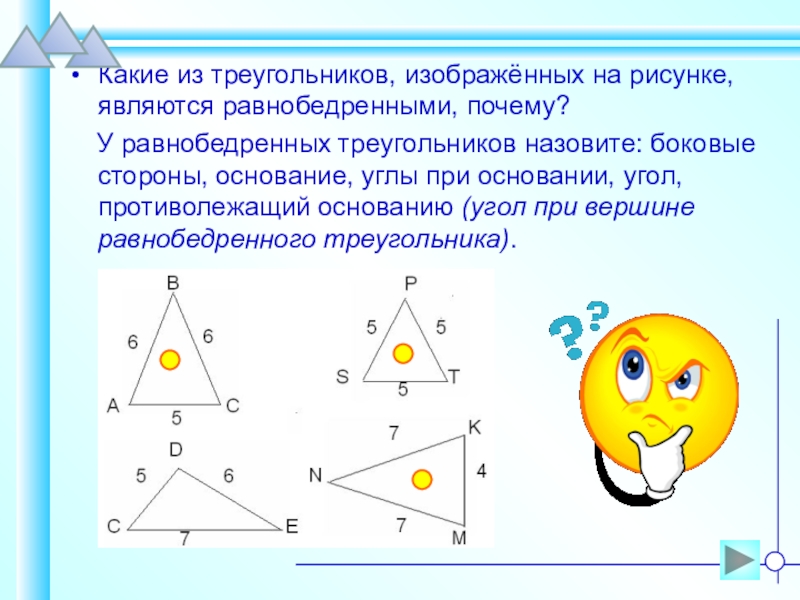
- 11. Какие из треугольников, изображённых на рисунке, являются
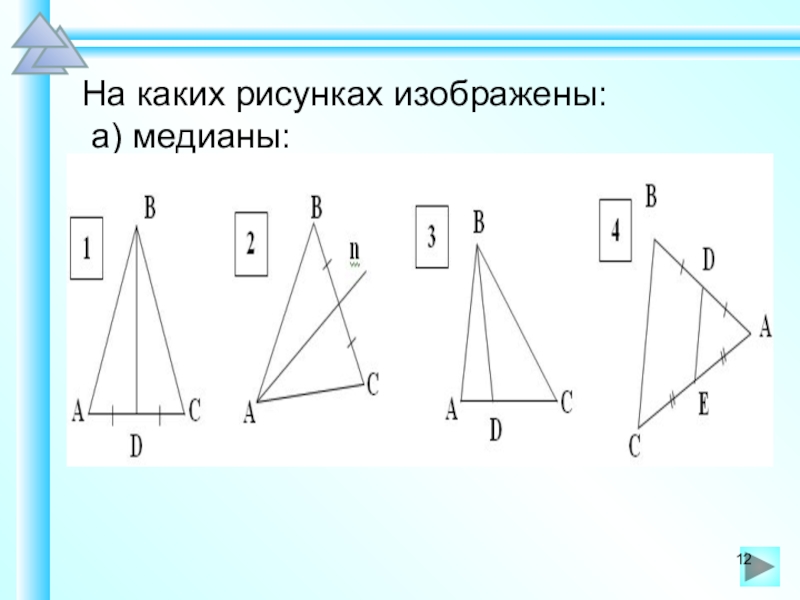
- 12. На каких рисунках изображены: а) медианы:
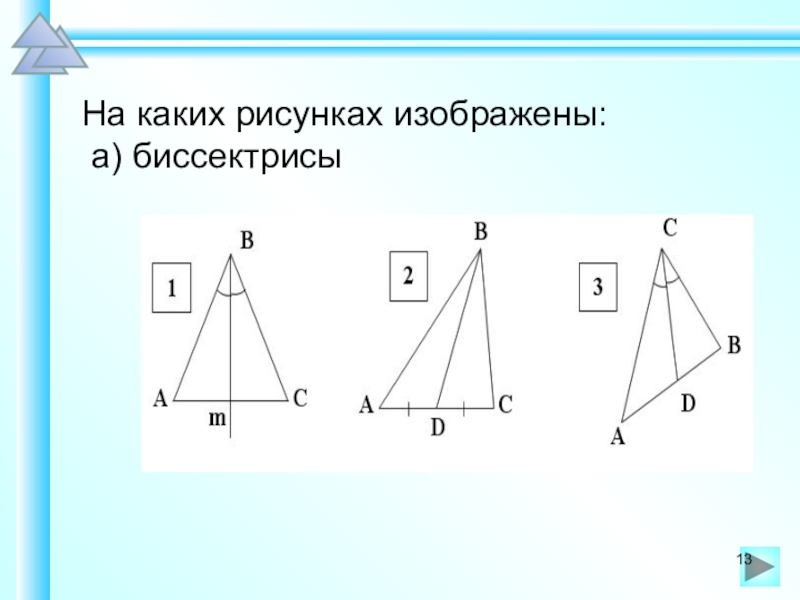
- 13. На каких рисунках изображены: а) биссектрисы
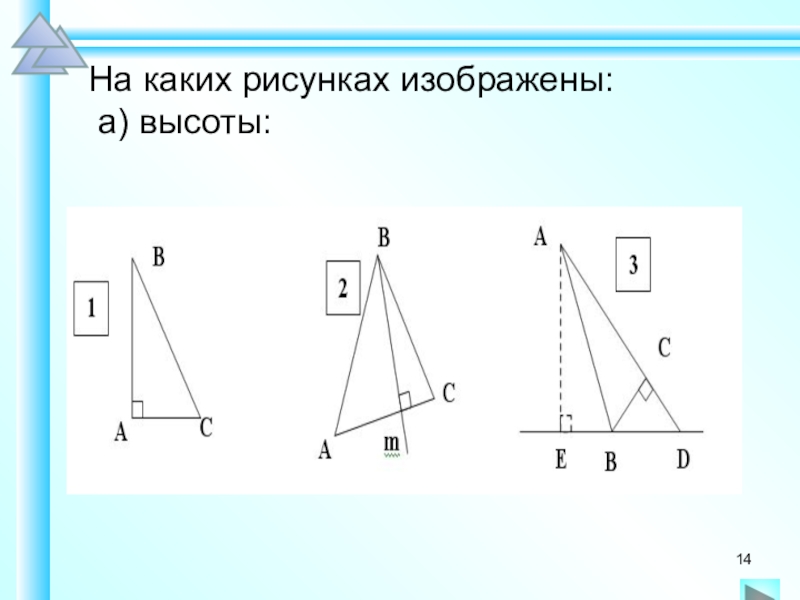
- 14. На каких рисунках изображены: а) высоты:
- 15. Решение задач В равнобедренном треугольнике
- 16. ЛАБОРАТОРНО-ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА «РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК И ЕГО СВОЙСТВА»
- 17. Ход работы: 1. Перед вами
- 18. Слайд 18
- 19. Выводы:У равнобедренного треугольника боковые стороны равны.Не всякая
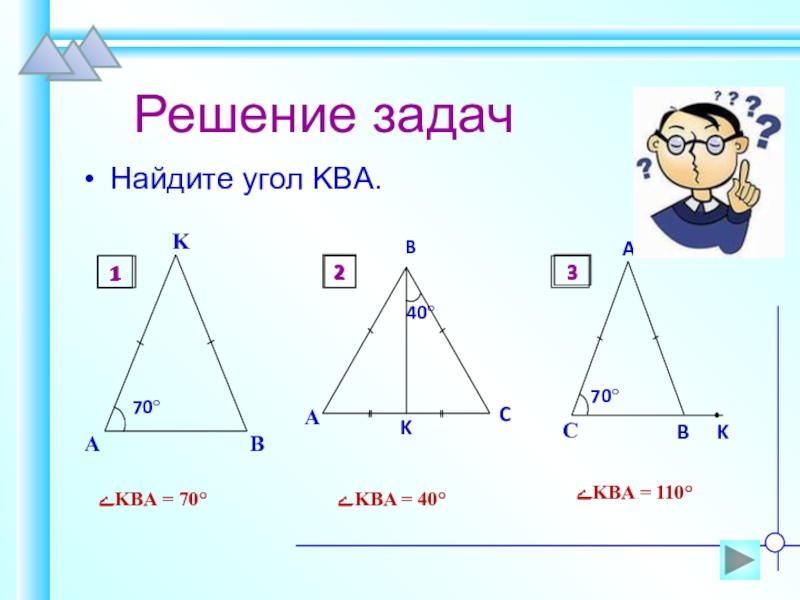
- 20. Решение задачНайдите угол KBA.ےKBA = 70° ےKBA = 40° ےKBA = 110°12 3
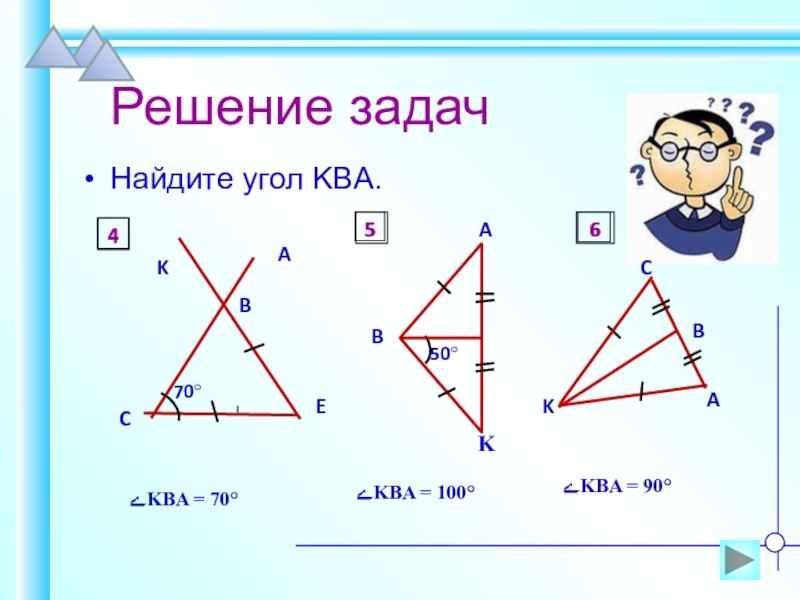
- 21. Решение задачНайдите угол KBA.ےKBA = 70°ےKBA = 100° ےKBA = 90°456
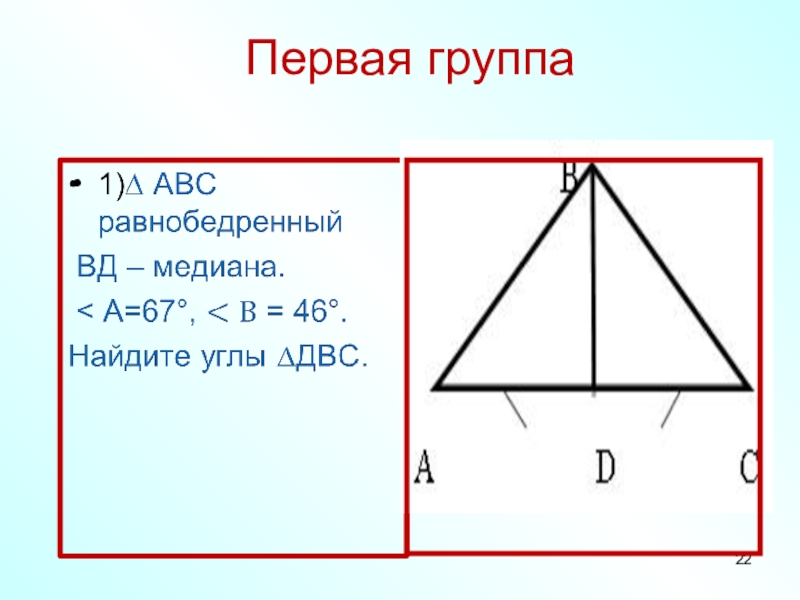
- 22. Первая группа
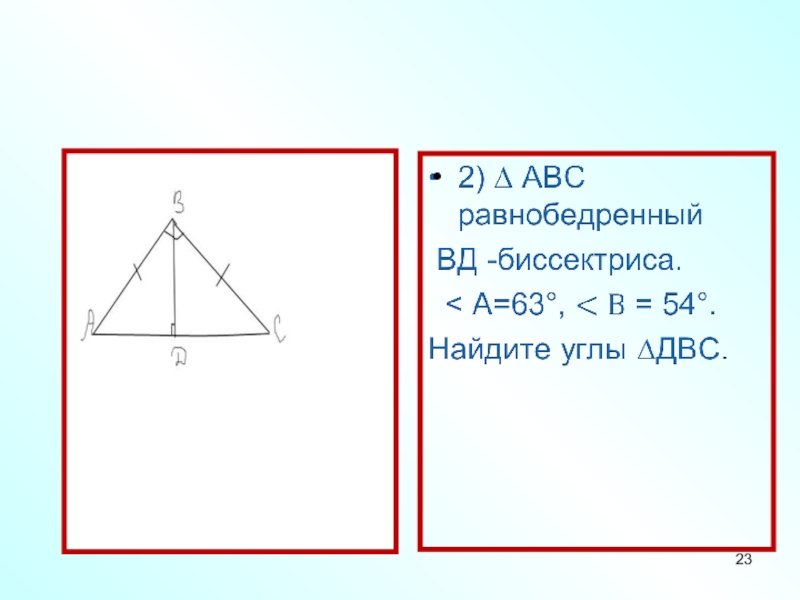
- 23.
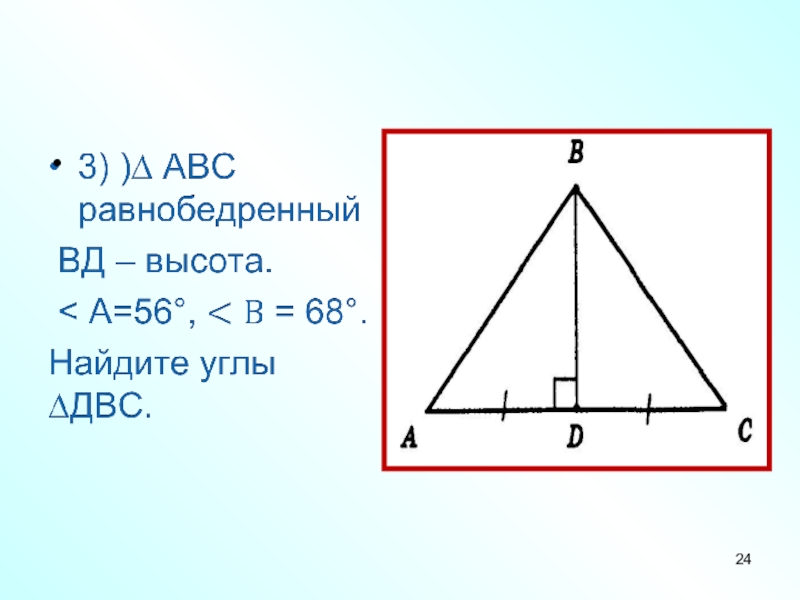
- 24.
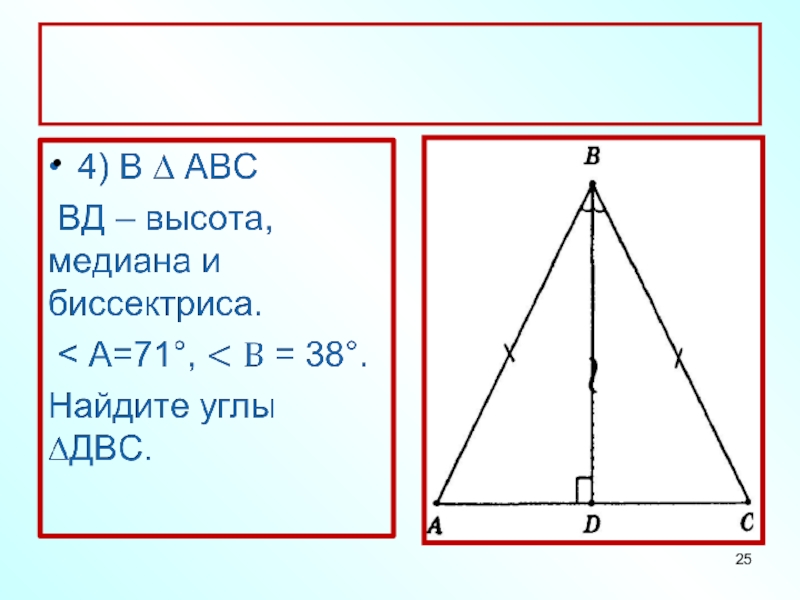
- 25.
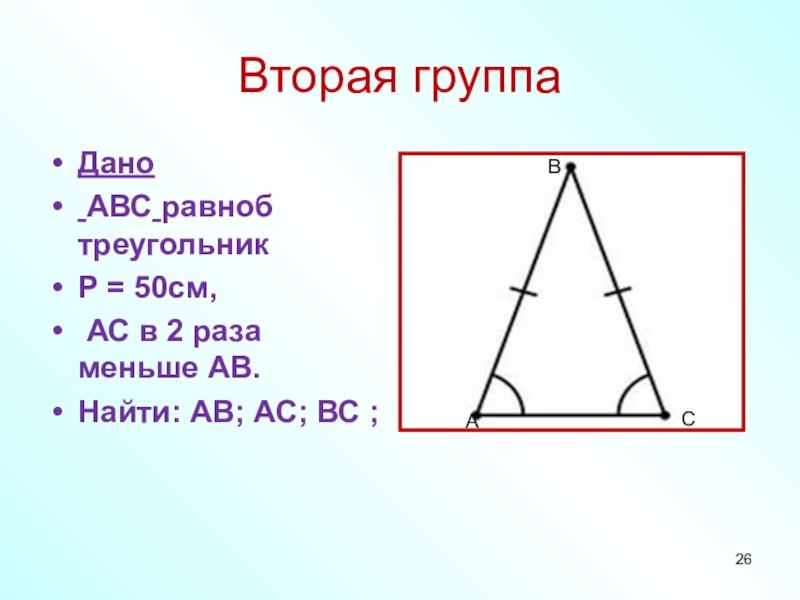
- 26. Вторая группаДано АВС равноб треугольникР = 50см,
- 27. Третья и четвертая группа№24 (1)В равнобедренном ∆
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Слайд 32
- 33. Слайд 33
- 34. Контрольные вопросыКакой треугольник называется равнобедренным?Каким свойством обладают
- 35. Домашнее задание.Теорема 3.5Задачи № 24(2), № 25 (1)
- 36. Достройте треугольник своего настроения
- 37. Спасибо за урок! Удачи!
Девиз нашего урока : «Есть в математике нечто,вызывающее восторг»На уроках геометрии очень важно уметь смотреть и видеть, замечать и отмечать различные особенности геометрических фигур.
Слайд 2Девиз нашего урока :
«Есть в математике нечто,
вызывающее восторг»
На уроках геометрии
очень важно уметь смотреть и видеть, замечать и
отмечать различные особенности
геометрических фигур.
отмечать различные особенности
геометрических фигур.
Слайд 3«Установка» :
«Развивать и тренировать своё геометрическое зрение.»
Кто ничего не замечает,
Тот
ничего не изучает.
Кто ничего не изучает,
Тот вечно хнычет и скучает.
Кто ничего не изучает,
Тот вечно хнычет и скучает.
Слайд 5 Треугольник – самая простая замкнутая
геометрическая фигура, одна из первых,
свойства которой
человек узнал ещё в
глубокой древности В одном египетском папирусе 4000-летней давности говорилось о площади равнобедренного треугольника. Через 2000 лет в Древней Греции очень активно велось изучение его свойств. Император Франции Наполеон свободное время посвящал занятиям математикой и, в частности, изучению свойств треугольников. Большой вклад в исследование треугольников внес знаменитый математик …,
глубокой древности В одном египетском папирусе 4000-летней давности говорилось о площади равнобедренного треугольника. Через 2000 лет в Древней Греции очень активно велось изучение его свойств. Император Франции Наполеон свободное время посвящал занятиям математикой и, в частности, изучению свойств треугольников. Большой вклад в исследование треугольников внес знаменитый математик …,
Слайд 6
Из дошедших до нас сочинений Евклида наиболее знамениты «Начала»,
состоящие из 15
книг.
В 1-й книге изучаются свойства треугольников
В 1-й книге изучаются свойства треугольников
ЕВКЛИД
Древнегреческий математик.
Дата рождения:
ок. 325 года до н.э.
Научная сфера:
математика
Известен как:
«Отец Геометрии»
Слайд 11Какие из треугольников, изображённых на рисунке, являются равнобедренными, почему?
У
равнобедренных треугольников назовите: боковые стороны, основание, углы при основании, угол, противолежащий основанию (угол при вершине равнобедренного треугольника).
Слайд 15 Решение задач
В равнобедренном треугольнике боковая сторона равна 9см,
а основание 5см. Вычислите периметр треугольника.
В равнобедренном треугольнике основание равно 7см, а периметр равен 17см. Вычислите боковую сторону треугольника.
В равнобедренном треугольнике боковая сторона равна 6см, а периметр 22см. Вычислите основание треугольника.
В равнобедренном треугольнике основание равно 7см, а периметр равен 17см. Вычислите боковую сторону треугольника.
В равнобедренном треугольнике боковая сторона равна 6см, а периметр 22см. Вычислите основание треугольника.
Слайд 17 Ход работы: 1. Перед вами равнобедренный треугольник АВС.( АС –основание) 2.Методом измерения исследуйте
треугольник : ( проведите медиану ВМ; измерьте угол АМВ и угол СМВ; измерьте угол АВМ и угол СВМ)
4.Полученные результаты занести в тетрадь.
5.Сделайте выводы.
Слайд 19Выводы:
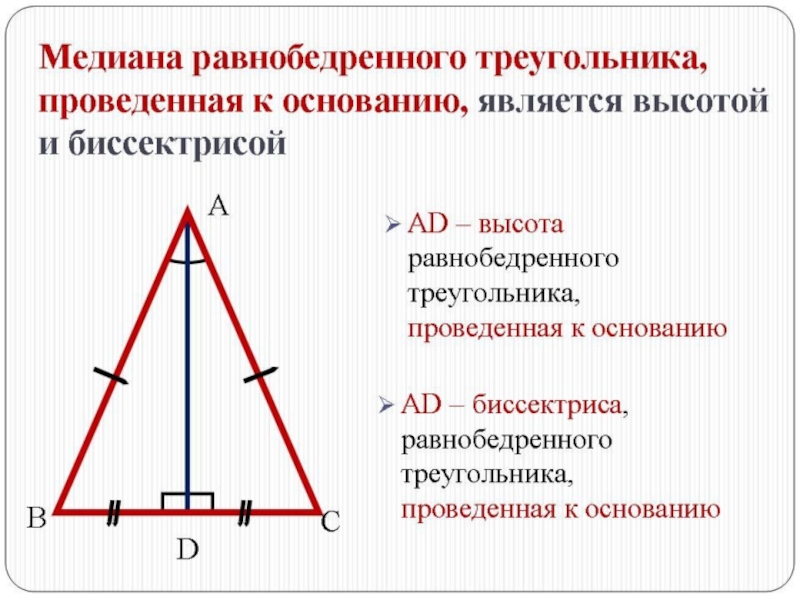
У равнобедренного треугольника боковые стороны равны.
Не всякая медиана равнобедренного треугольника является
биссектрисой и высотой, а только та, которая проведена из вершины к основанию.
Углы равнобедренного треугольника при основании равны.
Углы равнобедренного треугольника при основании равны.
Слайд 26Вторая группа
Дано
АВС равноб треугольник
Р = 50см,
АС в 2
раза меньше АВ.
Найти: АВ; АС; ВС ;
Найти: АВ; АС; ВС ;
А
В
С
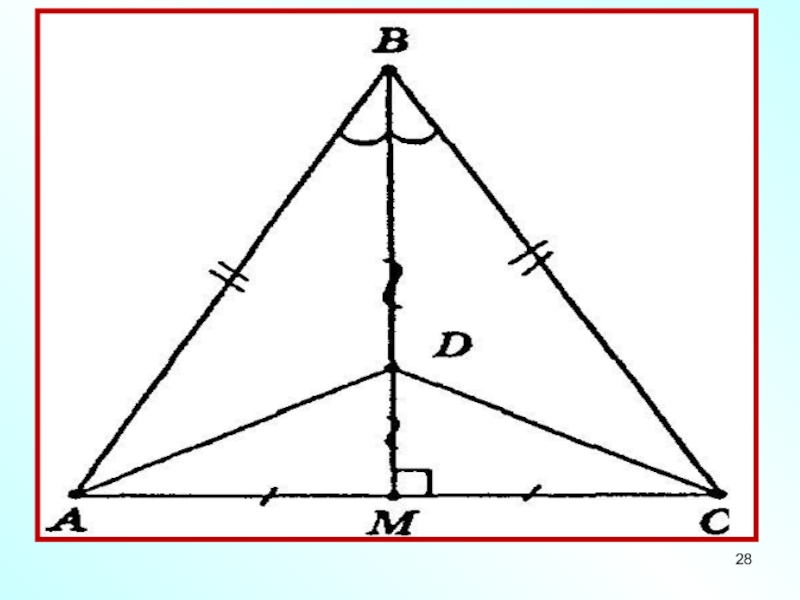
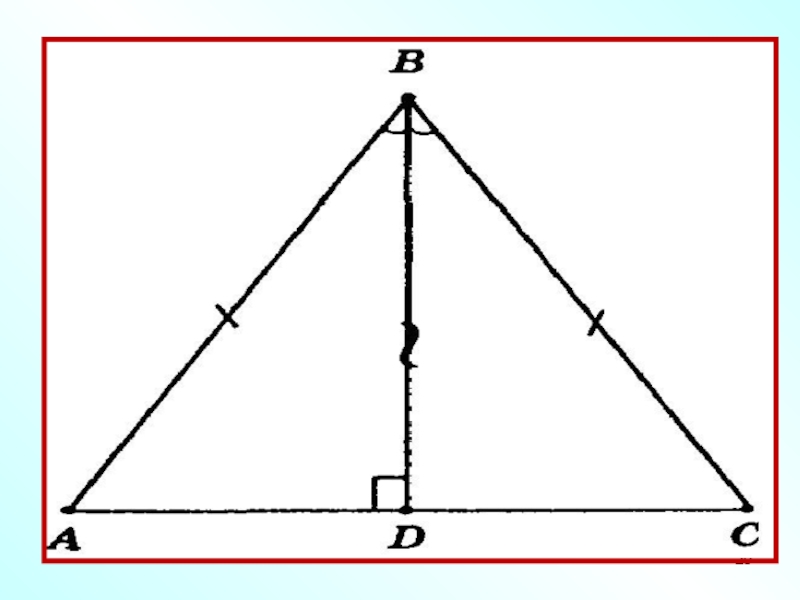
Слайд 27Третья и четвертая группа
№24 (1)
В равнобедренном ∆ АВС проведена медиана ВМ.
На ней взята точка Д.
Докажите, что
∆ АВД = ∆ СВД.
Докажите, что
∆ АВД = ∆ СВД.
№ 25 (2)
В ∆ АВС ,
ВД – высота и биссектриса.
Докажите, что ∆ АВС - равнобедренный
Слайд 34Контрольные вопросы
Какой треугольник называется равнобедренным?
Каким свойством обладают углы
в равнобедренном
треугольнике?
Каким свойством обладает медиана, проведённая к основанию равнобедренного треугольника?
Каким свойством обладает медиана, проведённая к основанию равнобедренного треугольника?
