- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Осевая симметрия (9 класс)
Содержание
- 1. Осевая симметрия (9 класс)
- 2. Осева́я симме́три́я — тип симметрии, имеющий несколько отличающихся определений:Отражательная
- 3. Вращательная симметрия.В естественных науках под осевой симметрией понимают вращательную симметрию (другие
- 4. Осевая симметрия n-го порядка — симметричность относительно поворотов на угол
- 5. ПримерыДве точки А и А1 называются симметричными друг другу относительно прямой m,
- 6. ПримерыКвадрат ABCD имеет четыре оси симметрии: прямые m, l, k и s.Если квадрат
- 7. ПримерыОкружность с центром в точке О и
- 8. Спасибо за внимание!!!
Осева́я симме́три́я — тип симметрии, имеющий несколько отличающихся определений:Отражательная симметрия. В евклидовой геометрии осевая симметрия — вид движения (зеркального отражения), при котором множеством неподвижных точек является пряма, называемая осью симметрии. Отсюда следует, что любой точке соответствует точка, находящаяся на том же расстоянии от оси симметрии, и
Слайд 1Осевая симметрия
Подготовил учитель математики,
МБОУ СОШ №12 города Воронежа,
Кузнецова Светлана Владимировна
Слайд 2Осева́я симме́три́я — тип симметрии, имеющий несколько отличающихся определений:
Отражательная симметрия. В евклидовой геометрии осевая симметрия —
вид движения (зеркального отражения), при котором множеством неподвижных точек является пряма, называемая осью симметрии. Отсюда следует, что любой точке соответствует точка, находящаяся на том же расстоянии от оси симметрии, и лежащая на одной прямой с исходной точкой и их общей проекцией на ось симметрии. Например, плоская фигура прямоугольник в пространстве осесимметрична и имеет 3 оси симметрии (две — в плоскости фигуры), если это не квадрат, а параллелограмм общего вида имеет одну ось симметрии (перпендикулярно плоскости).
Определение
Слайд 3Вращательная симметрия.В естественных науках под осевой симметрией понимают вращательную симметрию (другие термины — радиальная, аксиальная, лучевая симметрии) относительно поворотов вокруг
прямой. При этом тело (фигуру, задачу, организм) называют осесимметричными, если они переходят в себя при любом (например, малом) повороте вокруг этой прямой. В этом случае, прямоугольник не будет осесимметричным телом, но, например, конус будет.
Применительно к плоскости эти два вида симметрии совпадают (считаем, что ось тоже принадлежит этой плоскости).
Применительно к плоскости эти два вида симметрии совпадают (считаем, что ось тоже принадлежит этой плоскости).
Определение
Слайд 4Осевая симметрия n-го порядка — симметричность относительно поворотов на угол 360°/n вокруг какой-либо оси.
Описывается группой Zn.
Тогда симметрия в первом смысле (см. выше) является осевой симметрией второго порядка, а во втором — ∞-го порядка, так как поворот на любой сколь угодно малый угол приводит к совмещению фигуры с самой собой. Примеры: шар, цилиндр, конус.
Оси симметрии 2-го, 3-го, 4-го, 6-го и даже 5-го порядка (кристаллы с непериодическим пространственным расположением атомов (мозаика Пенроуза)) можно наблюдать на примере кристаллов.
Зеркально поворотная осевая симметрия n-го порядка — поворот на 360°/n и отражение в плоскости, перпендикулярной данной оси.
Оси симметрии порядка выше 2-го называются осями симметрии высшего порядка.
Тогда симметрия в первом смысле (см. выше) является осевой симметрией второго порядка, а во втором — ∞-го порядка, так как поворот на любой сколь угодно малый угол приводит к совмещению фигуры с самой собой. Примеры: шар, цилиндр, конус.
Оси симметрии 2-го, 3-го, 4-го, 6-го и даже 5-го порядка (кристаллы с непериодическим пространственным расположением атомов (мозаика Пенроуза)) можно наблюдать на примере кристаллов.
Зеркально поворотная осевая симметрия n-го порядка — поворот на 360°/n и отражение в плоскости, перпендикулярной данной оси.
Оси симметрии порядка выше 2-го называются осями симметрии высшего порядка.
Определение
Слайд 5Примеры
Две точки А и А1 называются симметричными друг другу относительно прямой m, если прямая m перпендикулярна отрезку АА1 и проходит
через его середину. Прямую m называют осью симметрии.
При сгибании плоскости чертежа по прямой m – оси симметрии симметричные фигуры совместятся.
Прямоугольник имеет две оси симметрии.
Квадрат имеет четыре оси симметрии.
Любая прямая, проходящая через центр окружности, является ее осью симметрии. Окружность имеет бесконечное множество осей симметрии.
Точки А и А1 симметричны относительно прямой m, так как прямая m перпендикулярна отрезку АА1 и проходит через его середину.
m – ось симметрии.
При сгибании плоскости чертежа по прямой m – оси симметрии симметричные фигуры совместятся.
Прямоугольник имеет две оси симметрии.
Квадрат имеет четыре оси симметрии.
Любая прямая, проходящая через центр окружности, является ее осью симметрии. Окружность имеет бесконечное множество осей симметрии.
Точки А и А1 симметричны относительно прямой m, так как прямая m перпендикулярна отрезку АА1 и проходит через его середину.
m – ось симметрии.
Слайд 6Примеры
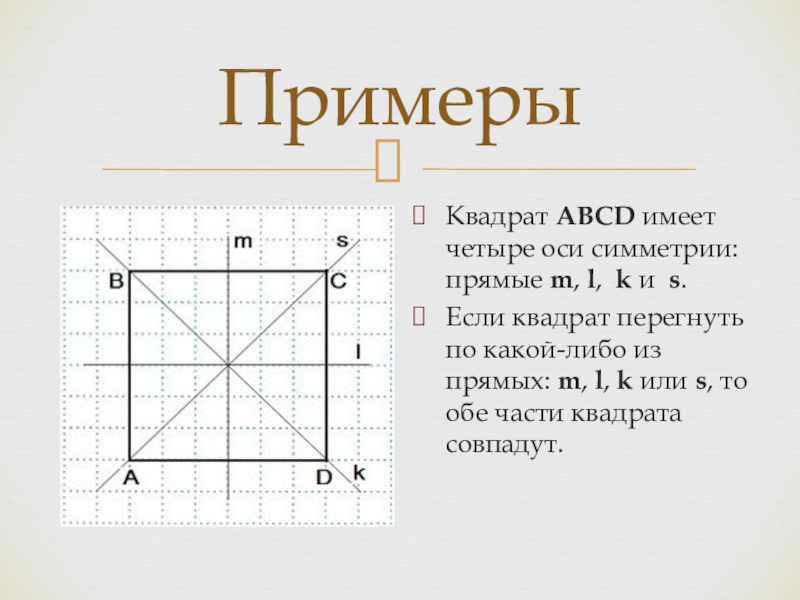
Квадрат ABCD имеет четыре оси симметрии: прямые m, l, k и s.
Если квадрат перегнуть по какой-либо из
прямых: m, l, k или s, то обе части квадрата совпадут.
Слайд 7Примеры
Окружность с центром в точке О и радиусом ОА имеет бесчисленное
количество осей симметрии. Это прямые: m, m1, m2, m3 ...