- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Монография по теме: Построение сечений тетраэдра и параллелепипеда
Содержание
- 1. Монография по теме: Построение сечений тетраэдра и параллелепипеда
- 2. Развитие пространственных представлений у учащихся. Сформировать умения
- 3. На слайде изображена картинка, которую в детстве
- 4. Построение сечений тетраэдра и параллелепипеда. Геометрия является
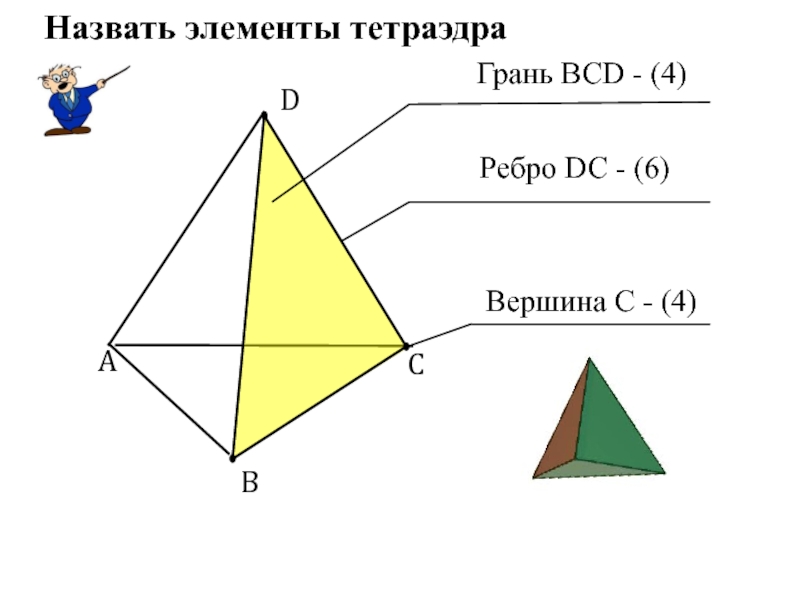
- 5. ABCDВершина С - (4) Назвать элементы тетраэдраРебро DC - (6) Грань ВСD - (4)
- 6. ADCBA1D1C1B1грань A₁B₁C₁D₁ - (6) ребро
- 7. 2. Какие две вершины называются противоположными?Назвать элементы
- 8. Назвать типы параллелепипедов:1. Прямоугольный параллелепипед2. Прямой параллелепипед.
- 9. Общие свойства параллелепипеда1. Противоположные грани равны и
- 10. Устный счет:Три измерения прямоугольного параллелепипеда равны 1
- 11. Заполнить таблицуДаДаДаДаДаДаДаДаДаДаДаДаДаНетНетНетРезультат: 8 правильных отв. -
- 12. Секущей плоскостью многогранника называетсялюбая плоскость, по обе
- 13. Т.к. тетраэдр имеет четыре грани, то в
- 14. Вспомним по готовым рисункам аксиомы и
- 15. 1. Соединять можно только две точки, лежащие
- 16. 1. Соединять можно только две точки, лежащие
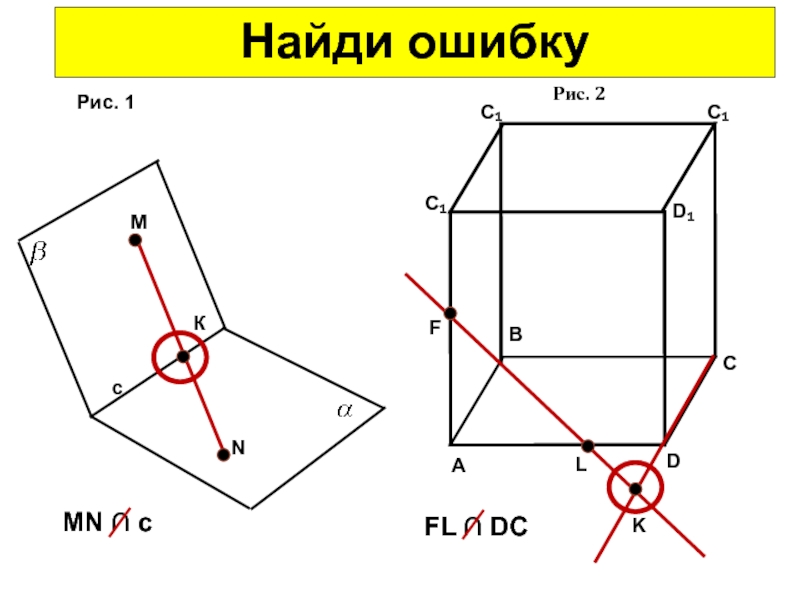
- 17. МNКсMN ∩ c = КРис. 1ABCDFLKFL ∩ DC = KРис. 2Найди ошибкуC₁C₁C₁D₁
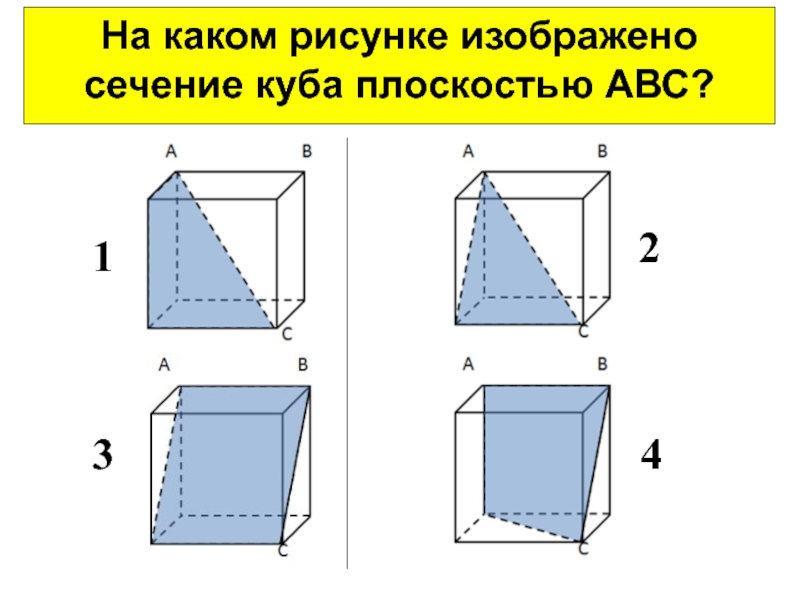
- 18. На каком рисунке изображено сечение куба плоскостью АВС?1432
- 19. Работа в парахЗадание: Найди ошибку на чертежеЗадание : Построить сечение через ребро параллелепипеда и точку N
- 20. 12Задание: Найди ошибку на чертежеПроверка работы в парах
- 21. Секущая плоскость пересекает противоположные грани параллелепипеда по
- 22. ТренажерыСамостоятельная работа«3»«4»«5»Построение сечений параллелепипеда123456Дополнительное заданиеПостроение сечений тетраэдра12345178910проверка11Основныеправила2
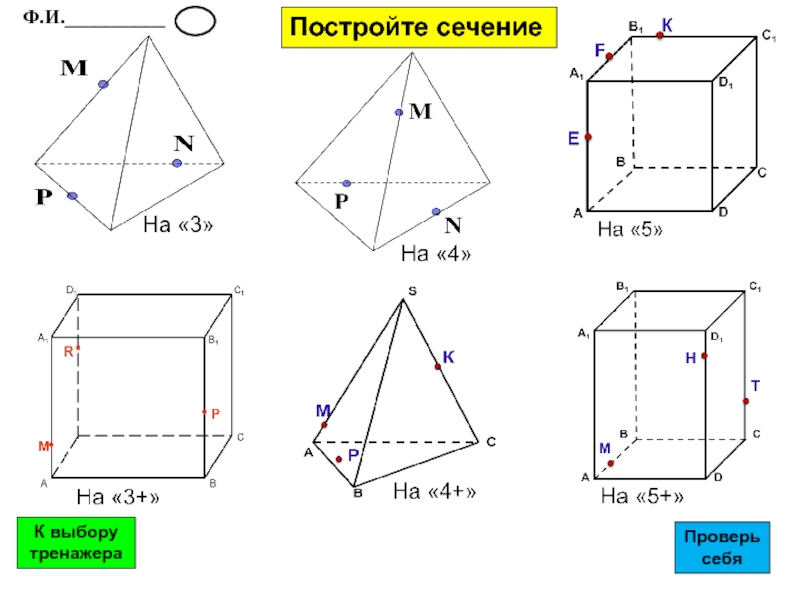
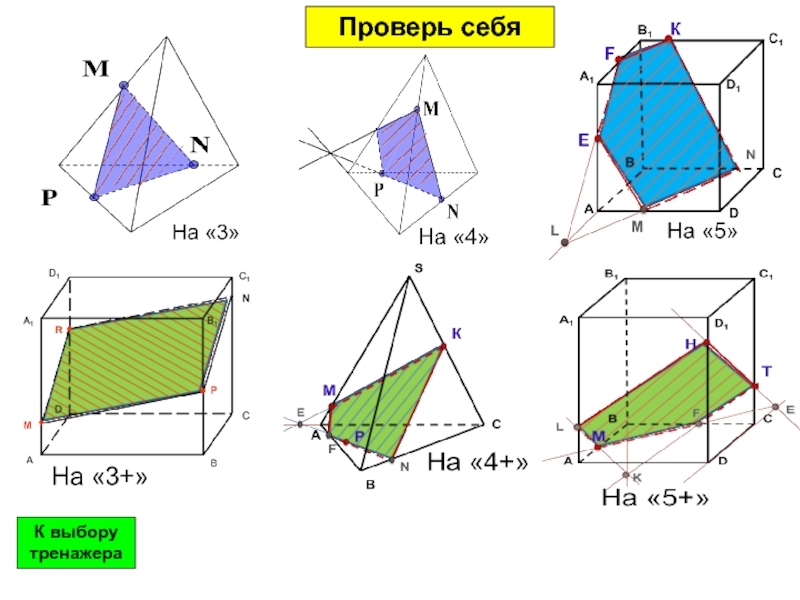
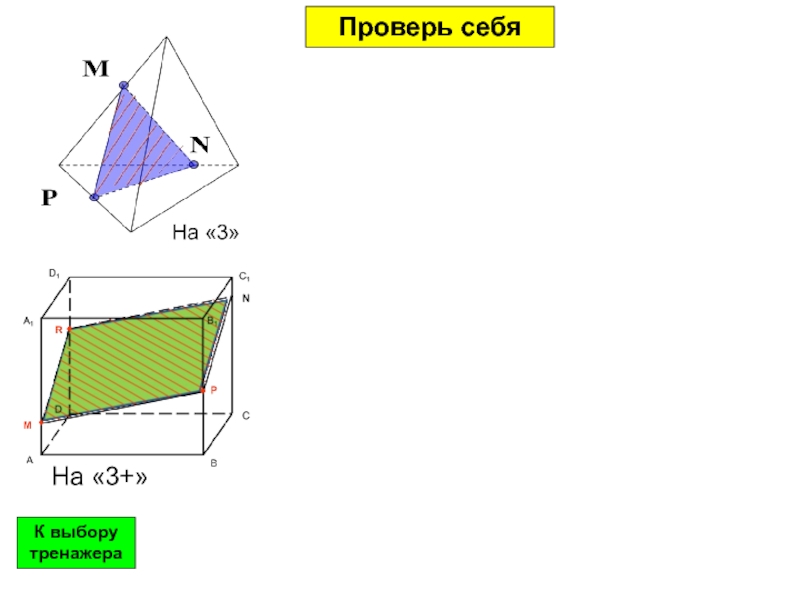
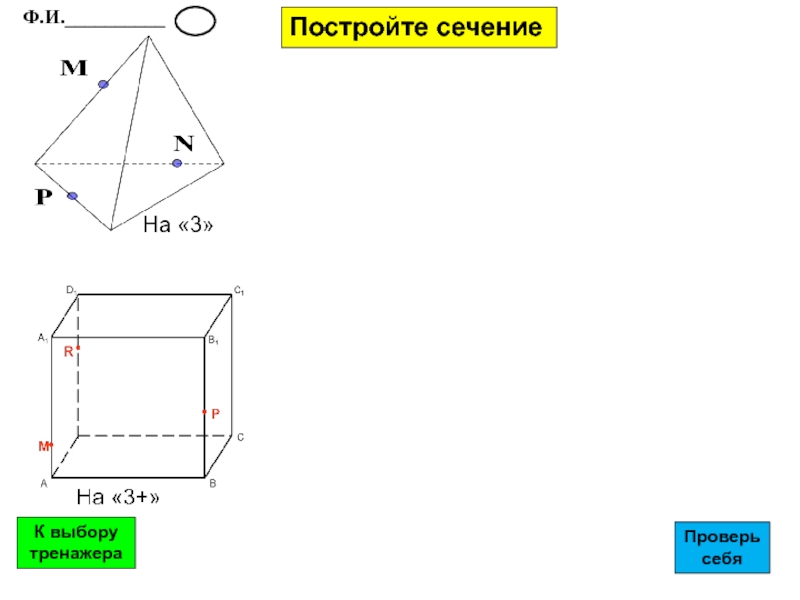
- 23. Постройте сечение Ф.И.__________К выбору тренажераПроверь себя
- 24. Проверь себяК выбору тренажера
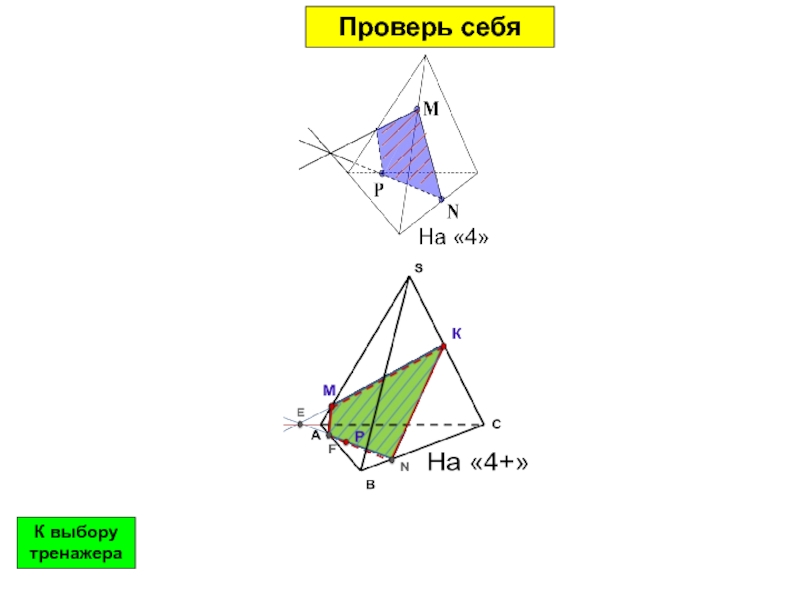
- 25. Проверь себяК выбору тренажера
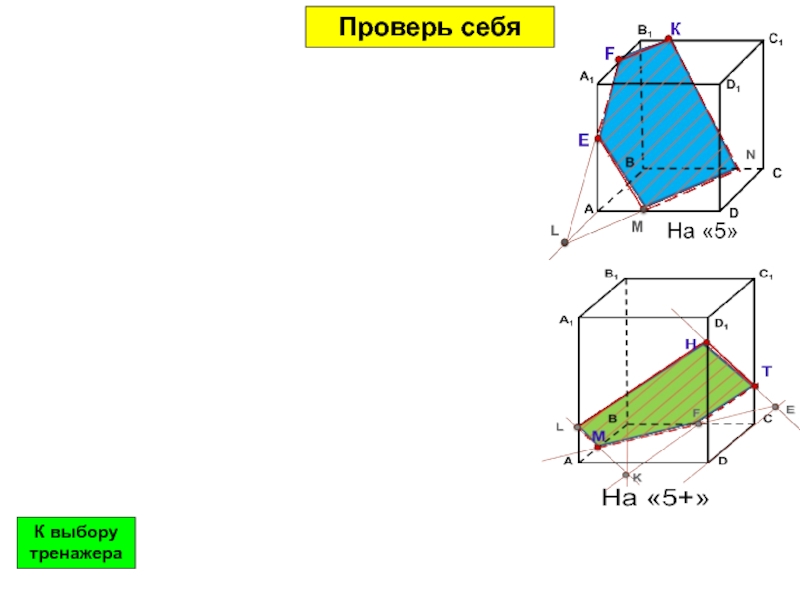
- 26. Проверь себяК выбору тренажера
- 27. Проверь себяК выбору тренажера
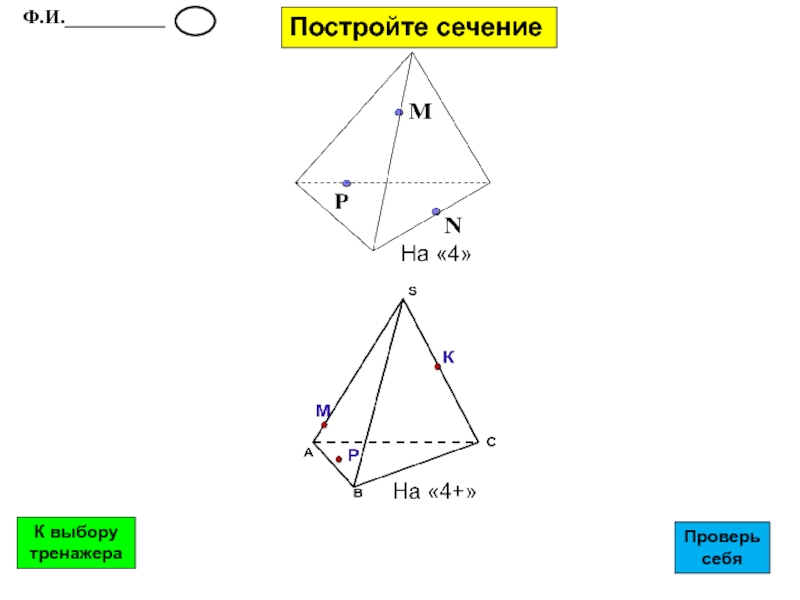
- 28. Постройте сечение Ф.И.__________К выбору тренажераПроверь себя
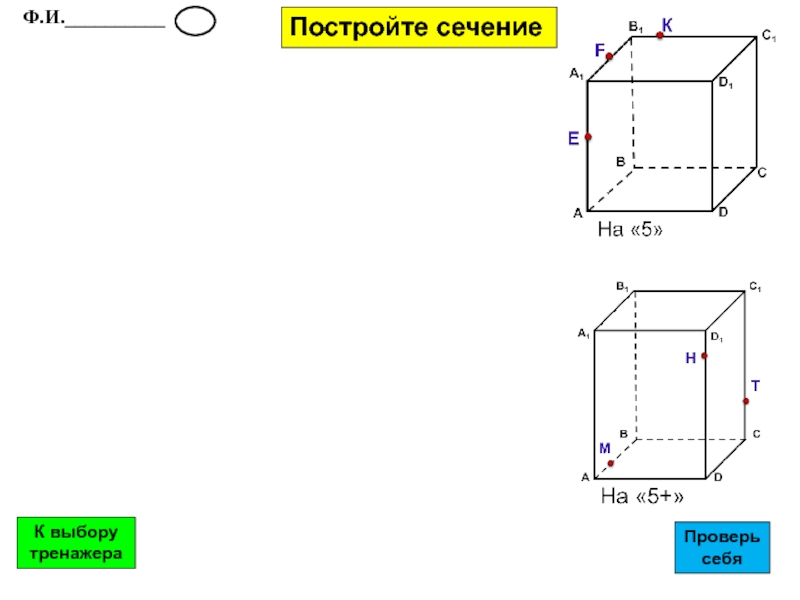
- 29. Постройте сечение Ф.И.__________К выбору тренажераПроверь себя
- 30. Постройте сечение Ф.И.__________К выбору тренажераПроверь себя
- 31. Практические примеры №1Построить сечение тетраэдра через ребро
- 32. ABCSMПостроить сечение тетраэдра, параллельное основанию через заданную точку M. KNПрактические примеры №2ОсновныеправилаК выбору тренажера
- 33. АСВSKPLТПостроить сечение тетраэдра через заданные точки К,
- 34. Воспользуемся правилами построения сечений. АСВSКМNТПостроить сечение тетраэдра
- 35. ABCDMNKПостроить сечение тетраэдра плоскостью МNК через точки
- 36. Построить сечение параллелепипеда плоскостью проходящей через точки А₁, С₁, В.Практические примеры №1ОсновныеправилаК выбору тренажера
- 37. Построить сечение параллелепипеда плоскостью проходящей через точки К, M, N.KNMПрактические примеры №2ОсновныеправилаК выбору тренажера
- 38. Построить сечение параллелепипеда плоскостью проходящей через точки К, M, N.Практические примеры №3ОсновныеправилаК выбору тренажера
- 39. Построить сечение параллелепипеда плоскостью проходящей через точки M, N, K.LPПрактические примеры №4ОсновныеправилаК выбору тренажера
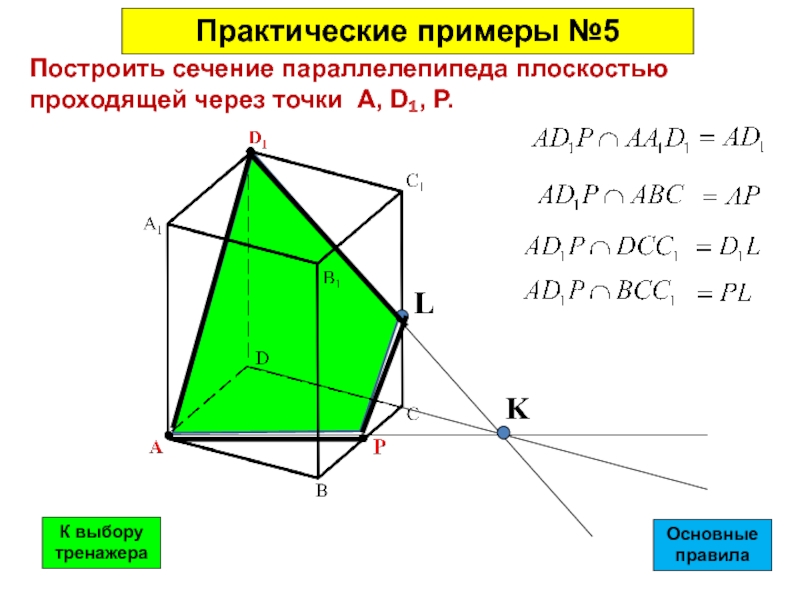
- 40. Построить сечение параллелепипеда плоскостью проходящей через точки А, D₁, P.KLПрактические примеры №5ОсновныеправилаК выбору тренажера
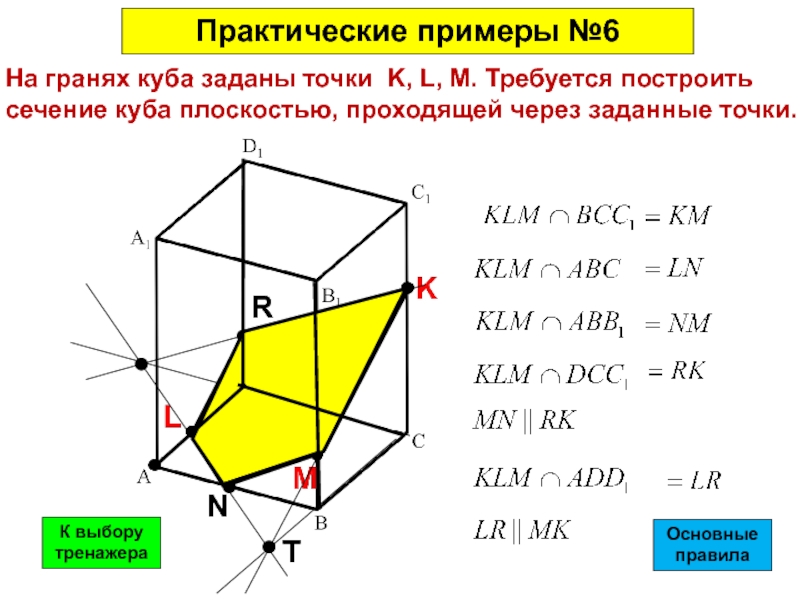
- 41. На гранях куба заданы точки K, L,
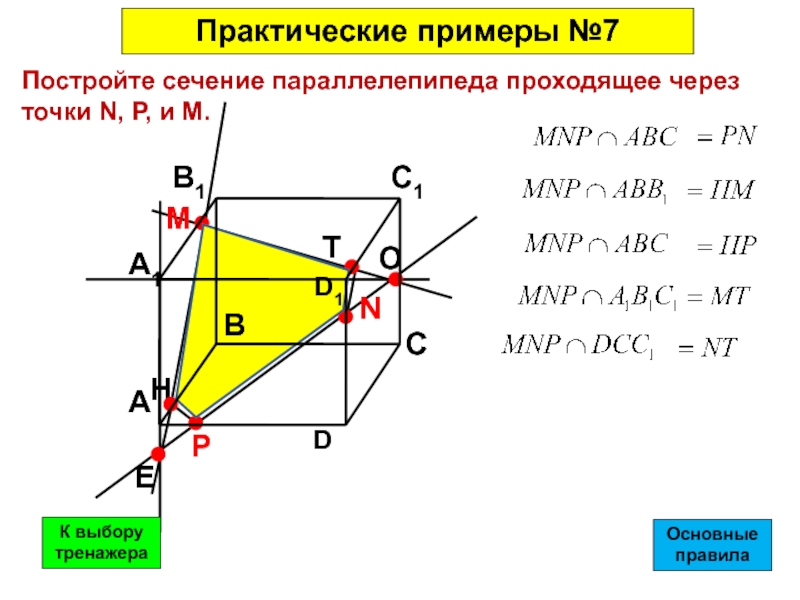
- 42. Постройте сечение параллелепипеда проходящее через точки N, Р, и М.Практические примеры №7ОсновныеправилаК выбору тренажера
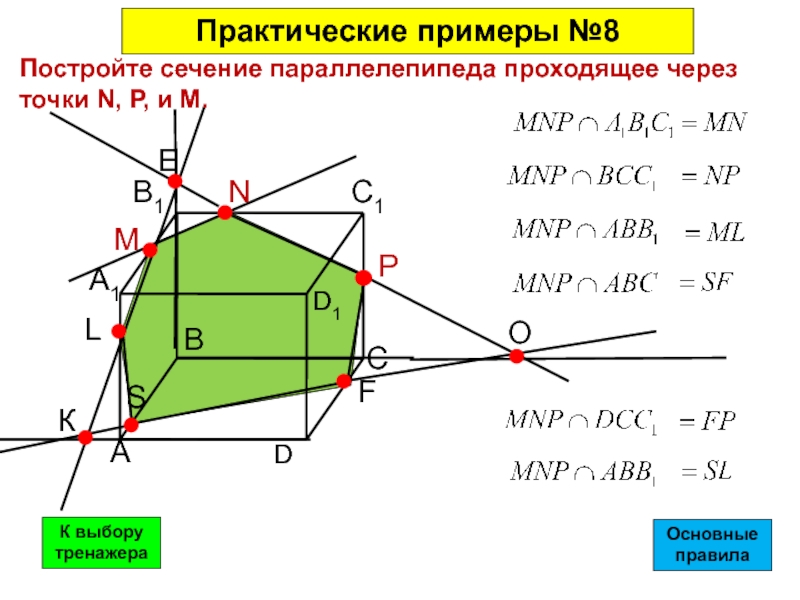
- 43. Постройте сечение параллелепипеда проходящее через точки N, Р, и М.Практические примеры №8ОсновныеправилаК выбору тренажера
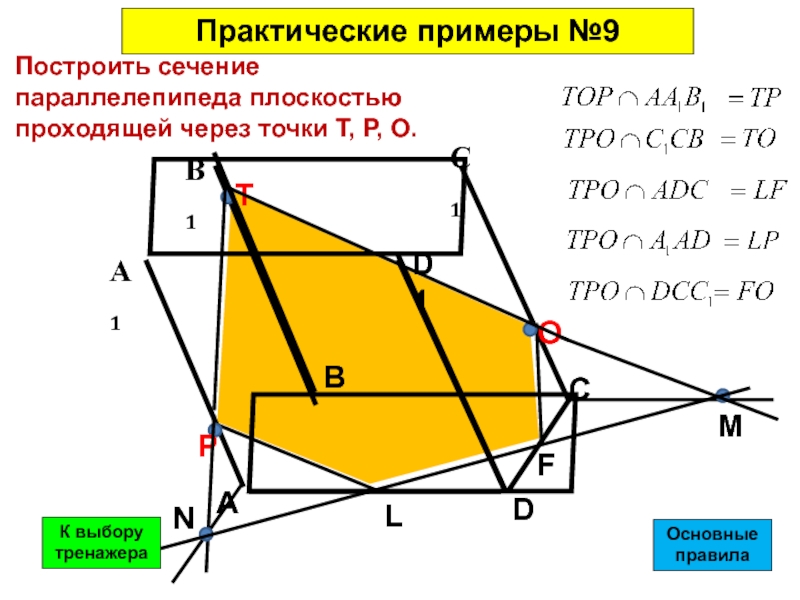
- 44. Построить сечение параллелепипеда плоскостью проходящей через точки T, P, O.Практические примеры №9ОсновныеправилаК выбору тренажера
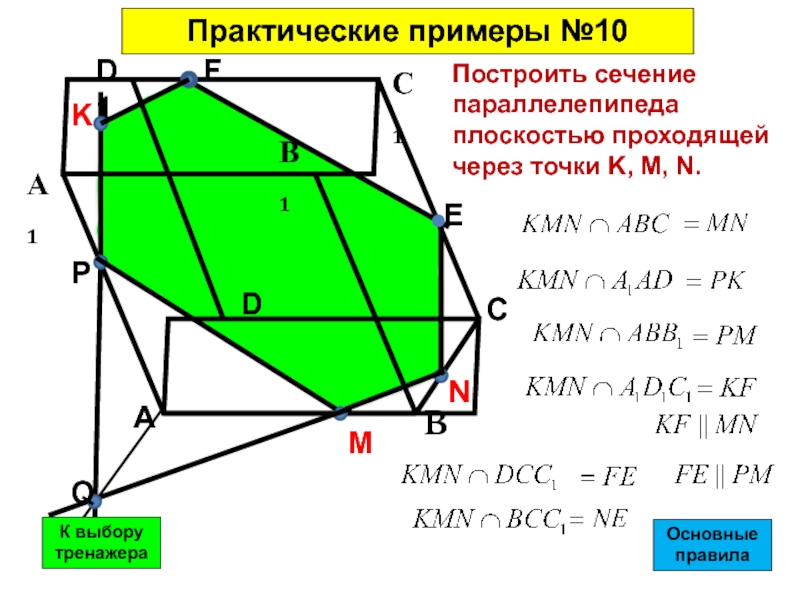
- 45. Построить сечение параллелепипеда плоскостью проходящей через точки K, M, N.Практические примеры №10ОсновныеправилаК выбору тренажера
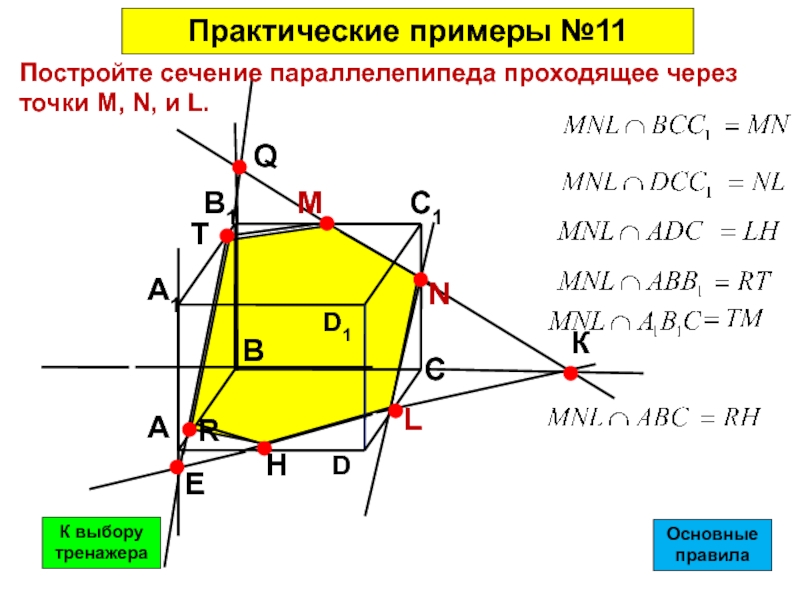
- 46. Постройте сечение параллелепипеда проходящее через точки М, N, и L.Практические примеры №11ОсновныеправилаК выбору тренажера
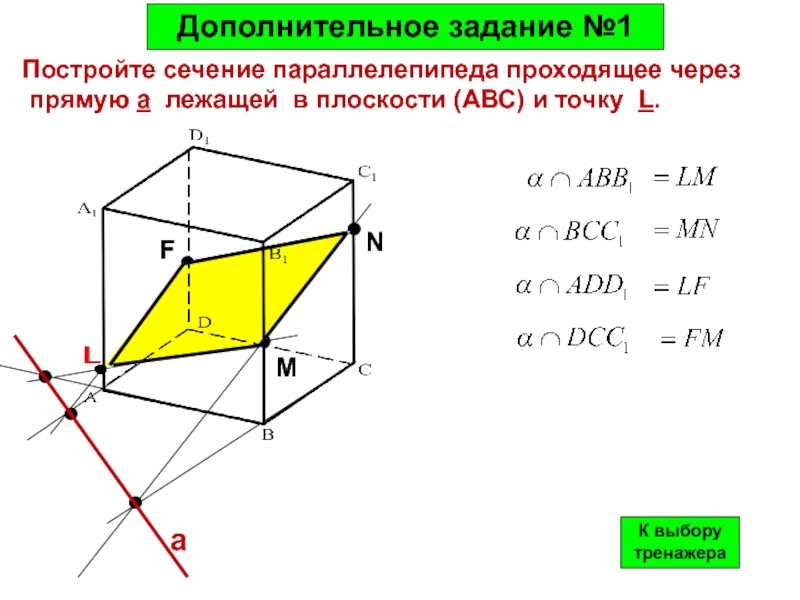
- 47. Дополнительное задание №1Постройте сечение параллелепипеда проходящее через
- 48. Дополнительное задание №2 из сборника ЕГЭК выбору
- 49. Домашнее задание§14, упражнение 79 (б). Выбери
- 50. К выбору тренажераРазминкагимнастика для глазКабинет, в котором
- 51. Литература и интернет ресурсы:Картинки1. Учебник. Геометрия: учебник
- 52. На новый урок
Слайд 1Кощеев ММ
Учитель математики
МКОУ «Погорельская СОШ»
Построение сечений тетраэдра и параллелепипеда.
Слайд 2Развитие пространственных представлений у учащихся.
Сформировать умения у учащихся строить сечения
Проверить уровень усвоения теоретических знаний по свойствам параллелепипеда
Формировать у обучающихся навык применения изученных свойств при решении задач и построений сечений
Рассмотреть возможные варианты сечений тетраэдра и параллелепипеда.
Познакомить с правилами построения сечений.
Показать на примерах решения задач на построение сечений тетраэдра и параллелепипеда.
Выработать навыки построения сечений тетраэдра и параллелепипеда при различных случаях задания секущей плоскости.
Цель работы:
Задачи:
Слайд 3На слайде изображена картинка, которую в детстве нарисовал Экзюпери, будущий великий
Как вы думаете, что изобразил юный художник?
На самом деле это был удав, проглотивший слона. Чтобы другие это поняли, юный художник выразился конкретнее и нарисовал второй рисунок. Он был уверен, что теперь-то все поймут, так как он объяснил взрослым свою картинку не только снаружи, но и изнутри.
Как же это удалось шестилетнему художнику?
Он мысленно разрезал удава и показал, что содержится внутри.
Вот и мы, сегодня будем строить сечения , но не рисунков, а геометрических фигур тетраэдра и параллелепипеда
Слайд 4Построение сечений тетраэдра и параллелепипеда.
Геометрия является самым могущественным средством для
Галилео Галилей
Слайд 6
A
D
C
B
A1
D1
C1
B1
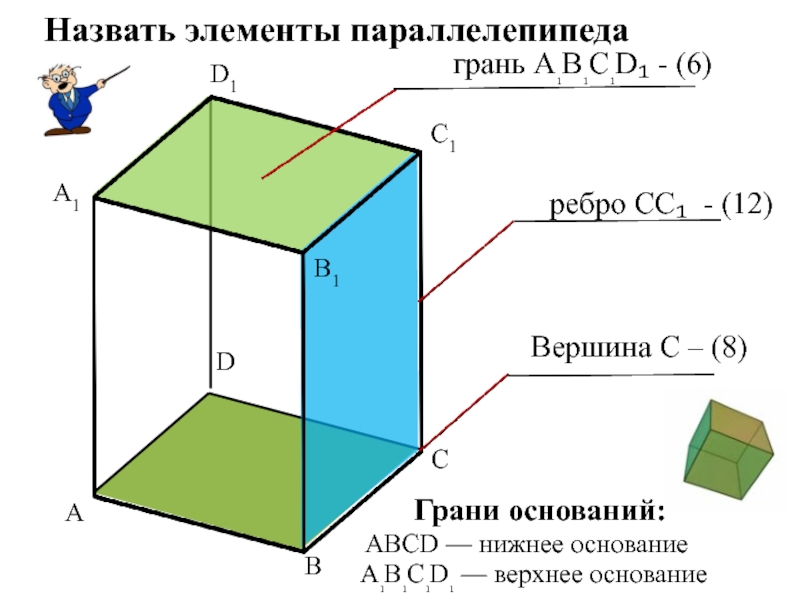
грань A₁B₁C₁D₁ - (6)
ребро СС₁ - (12)
Вершина С
ABCD — нижнее основание
A₁B₁C₁D₁ — верхнее основание
Грани оснований:
Назвать элементы параллелепипеда
Слайд 72. Какие две вершины называются противоположными?
Назвать элементы параллелепипеда
1. Какие две грани
3. Что называется диагональю параллелепипеда?
4. Что называется измерением параллелепипеда?
Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро - смежными.
Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными.
Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда.
Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями
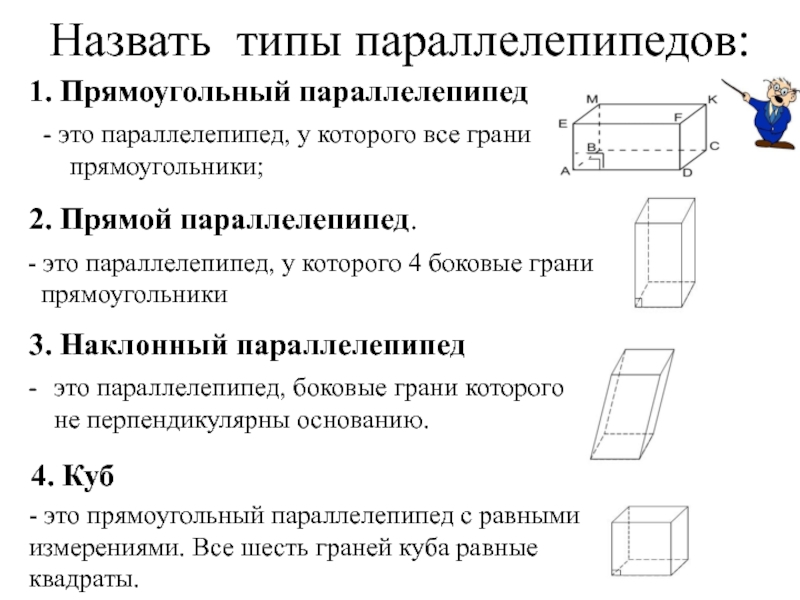
Слайд 8Назвать типы параллелепипедов:
1. Прямоугольный параллелепипед
2. Прямой параллелепипед.
3. Наклонный параллелепипед
4. Куб
прямоугольники;
- это параллелепипед, у которого 4 боковые грани
прямоугольники
это параллелепипед, боковые грани которого не перпендикулярны основанию.
- это прямоугольный параллелепипед с равными измерениями. Все шесть граней куба равные квадраты.
Слайд 9Общие свойства параллелепипеда
1. Противоположные грани равны и параллельны
2. Диагонали пересекаются в
Свойства прямоугольного параллелепипеда
1. В прямоугольном параллелепипеде все шесть граней – прямоугольники
2. Все двугранные углы прямоугольного параллелепипеда– прямые
3. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов
трех его измерений. d²=а²+b²+c²
Свойства прямого параллелепипеда
1. Боковые грани прямого параллелепипеда — прямоугольники.
4. Диагонали прямоугольного параллелепипеда равны
2. Диагонали прямого параллелепипеда вычисляются
по формулам: d²=а²+b²+с²+2∙а∙b∙cosα
5. Полная поверхность прямоугольного параллелепипеда S=2(аb+bc+ас)
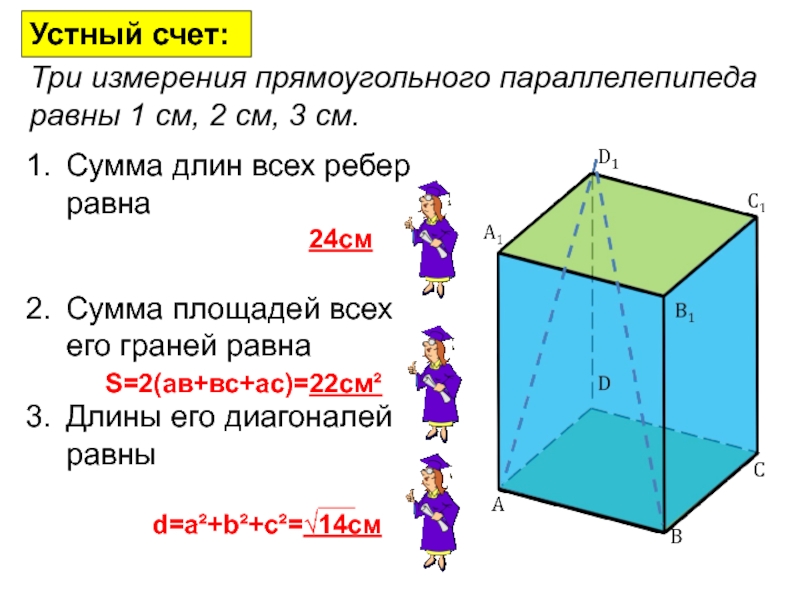
Слайд 10Устный счет:
Три измерения прямоугольного параллелепипеда равны 1 см, 2 см, 3
Сумма длин всех ребер равна
Сумма площадей всех его граней равна
Длины его диагоналей равны
24см
S=2(ав+вс+ас)=22см²
d=а²+b²+c²=√14см
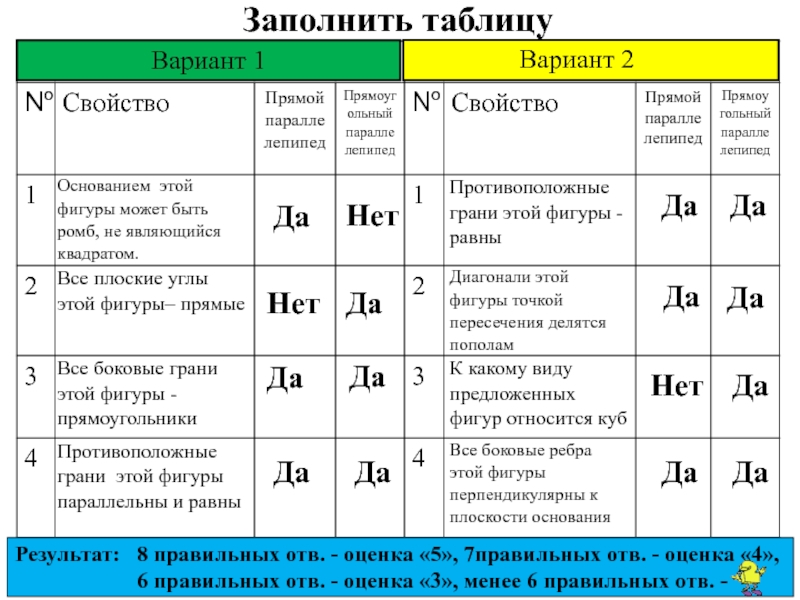
Слайд 11Заполнить таблицу
Да
Да
Да
Да
Да
Да
Да
Да
Да
Да
Да
Да
Да
Нет
Нет
Нет
Результат: 8 правильных отв. - оценка «5», 7правильных отв.
6 правильных отв. - оценка «3», менее 6 правильных отв. -
Вариант 2
Вариант 1
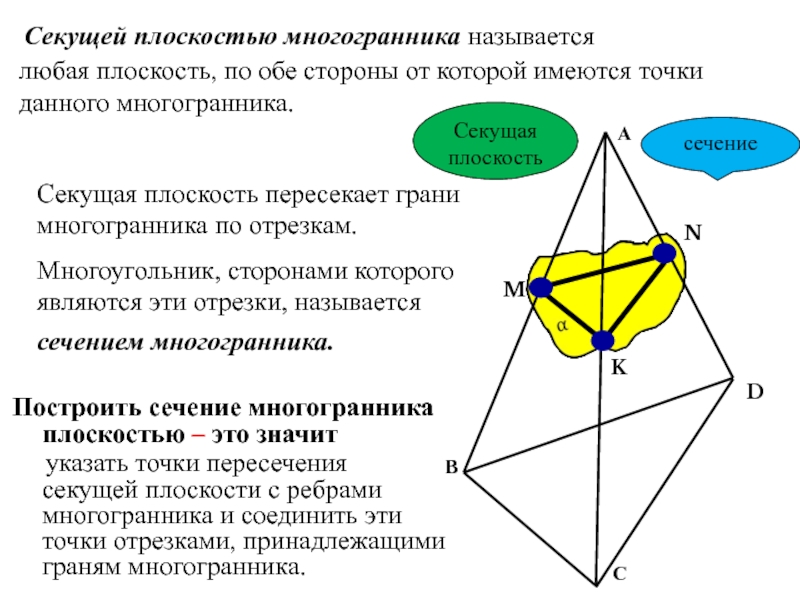
Слайд 12Секущей плоскостью многогранника называется
любая плоскость, по обе стороны от которой имеются
Секущая плоскость пересекает грани многогранника по отрезкам.
Многоугольник, сторонами которого являются эти отрезки, называется
Построить сечение многогранника плоскостью – это значит
указать точки пересечения секущей плоскости с ребрами многогранника и соединить эти точки отрезками, принадлежащими граням многогранника.
сечение
Секущая плоскость
сечением многогранника.
А
С
Слайд 13
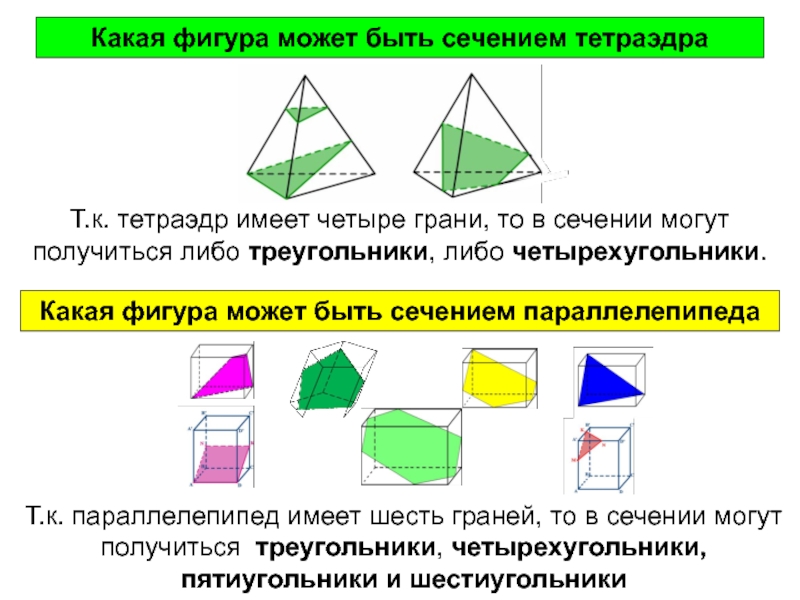
Т.к. тетраэдр имеет четыре грани, то в сечении могут получиться либо
Какая фигура может быть сечением тетраэдра
Какая фигура может быть сечением параллелепипеда
Т.к. параллелепипед имеет шесть граней, то в сечении могут получиться треугольники, четырехугольники, пятиугольники и шестиугольники
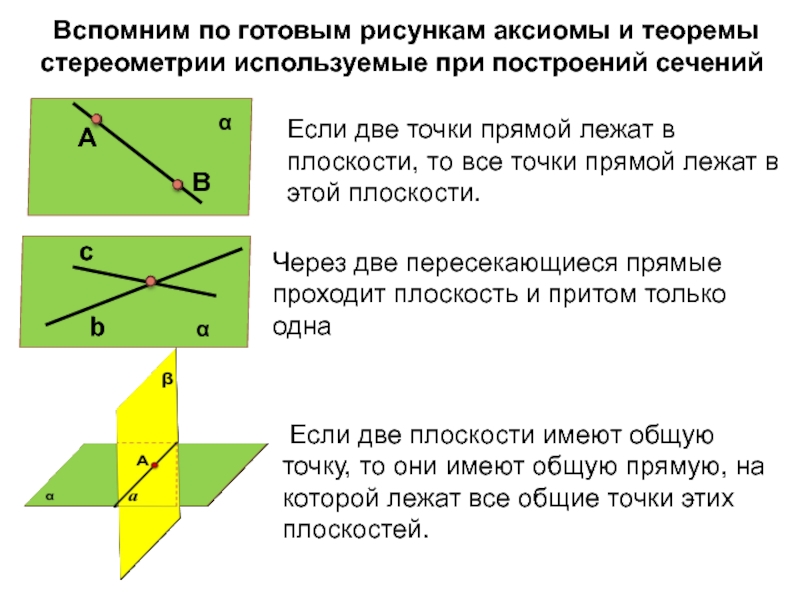
Слайд 14 Вспомним по готовым рисункам аксиомы и теоремы стереометрии используемые при
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
А
В
α
α
Через две пересекающиеся прямые проходит плоскость и притом только одна
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
с
b
Слайд 151. Соединять можно только две точки, лежащие в плоскости одной грани.
2.
3. Если в плоскости грани отмечена только одна точка, принадлежащая плоскости сечения, то надо построить дополнительную точку. Для этого необходимо найти точки пересечения уже построенных прямых с другими прямыми, лежащими в тех же гранях.
Т.е. Найти пересекающиеся прямые одной
плоскости и построить точку их пересечения
При построении сечений необходимо учитывать три правила:
Слайд 161. Соединять можно только две точки, лежащие в плоскости одной грани.
2.
3. Если в плоскости грани отмечена только одна точка, принадлежащая плоскости сечения, то надо построить дополнительную точку. Для этого необходимо найти точки пересечения уже построенных прямых с другими прямыми, лежащими в тех же гранях.
Т.е. Найти пересекающиеся прямые одной плоскости и построить точку их пересечения
При построении сечений необходимо учитывать три правила:
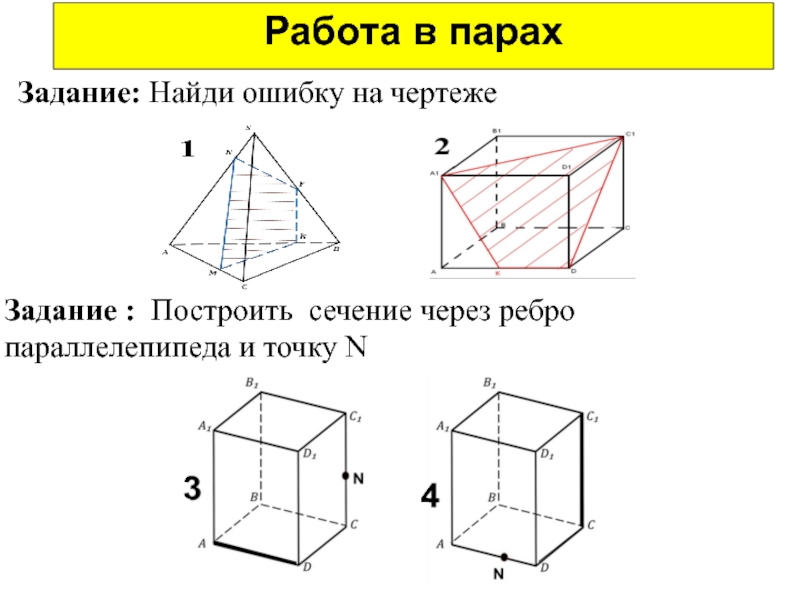
Слайд 19Работа в парах
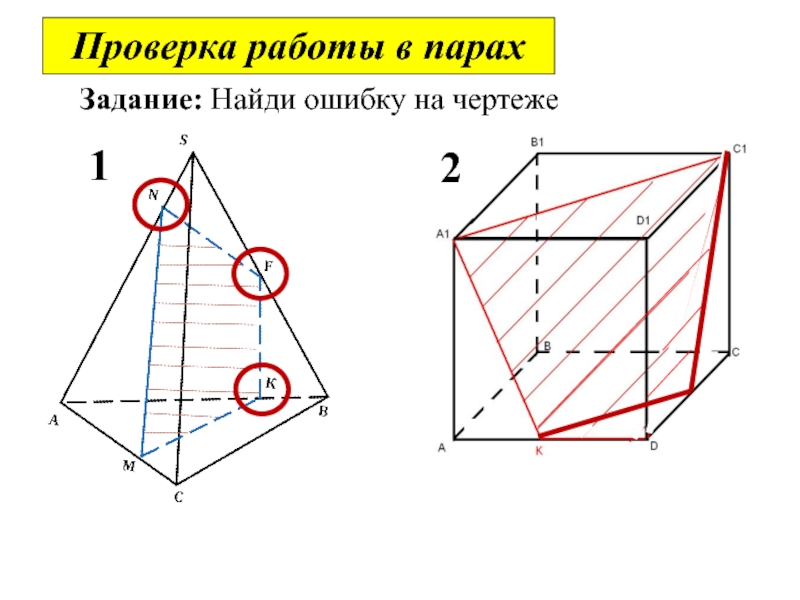
Задание: Найди ошибку на чертеже
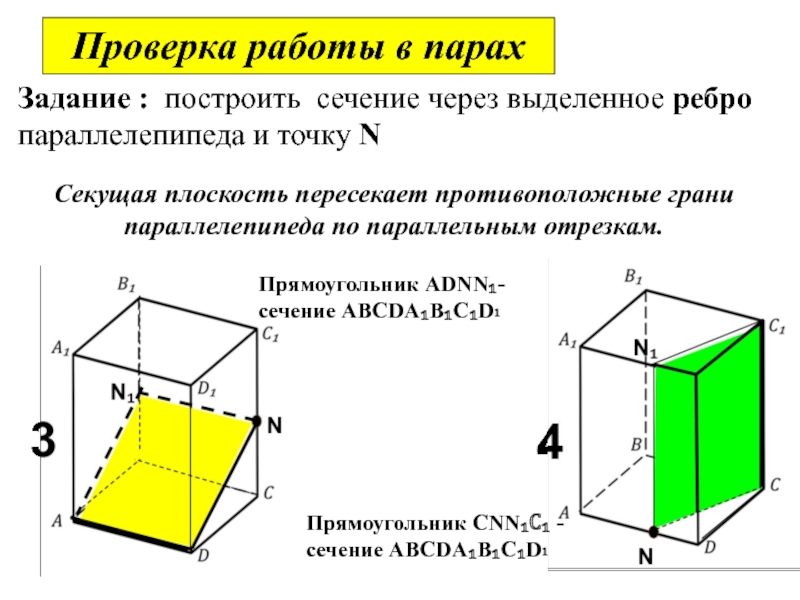
Задание : Построить сечение через
Слайд 21Секущая плоскость пересекает противоположные грани параллелепипеда по параллельным отрезкам.
Задание : построить
Проверка работы в парах
Прямоугольник ADNN₁- сечение ABCDA₁B₁C₁D₁
Прямоугольник CNN₁C₁ - сечение ABCDA₁B₁C₁D₁
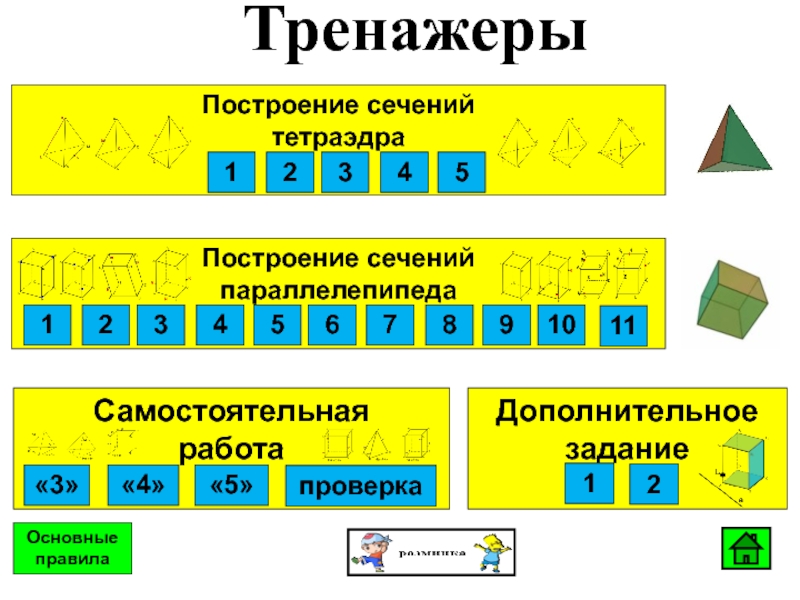
Слайд 22Тренажеры
Самостоятельная
работа
«3»
«4»
«5»
Построение сечений
параллелепипеда
1
2
3
4
5
6
Дополнительное задание
Построение сечений
тетраэдра
1
2
3
4
5
1
7
8
9
10
проверка
11
Основные
правила
2
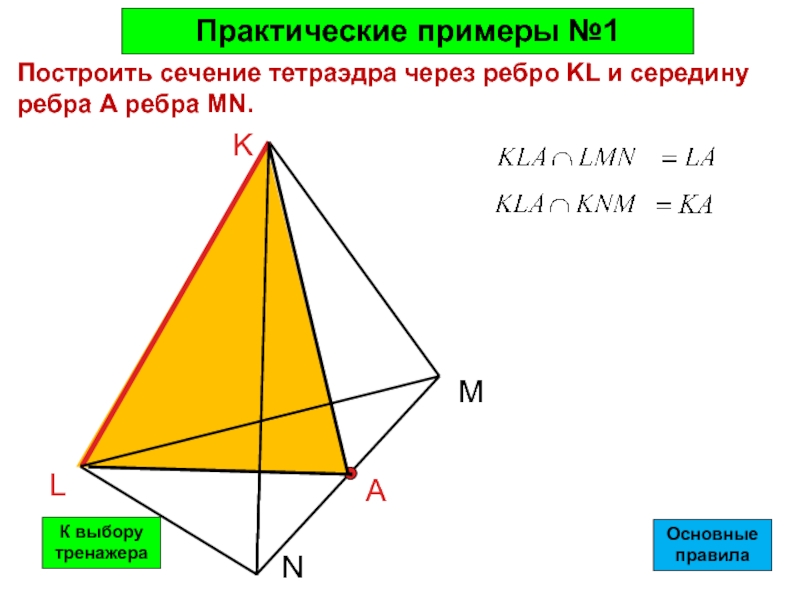
Слайд 31Практические примеры №1
Построить сечение тетраэдра через ребро KL и середину ребра
К выбору тренажера
Основные
правила
Слайд 32
A
B
C
S
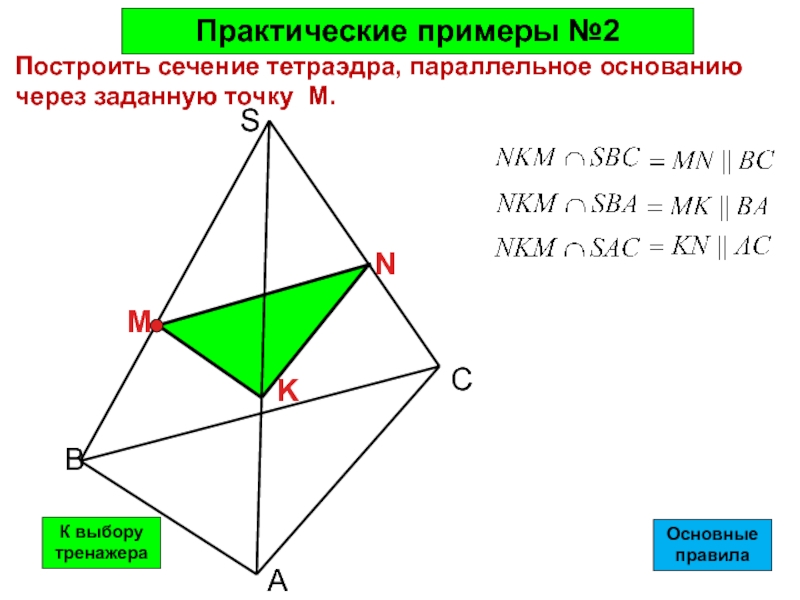
M
Построить сечение тетраэдра, параллельное основанию через заданную точку M.
K
N
Практические примеры
Основные
правила
К выбору тренажера
Слайд 33
А
С
В
S
K
P
L
Т
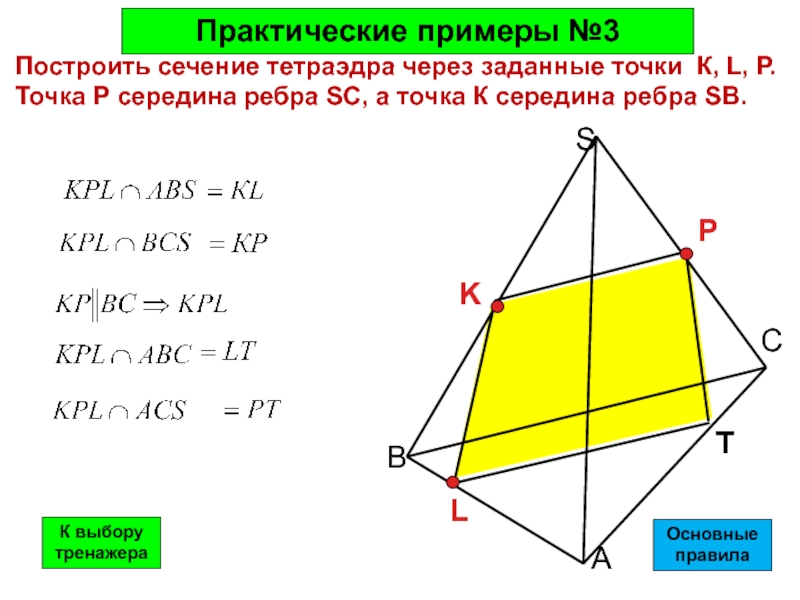
Построить сечение тетраэдра через заданные точки К, L, P. Точка Р
Практические примеры №3
Основные
правила
К выбору тренажера
Слайд 34
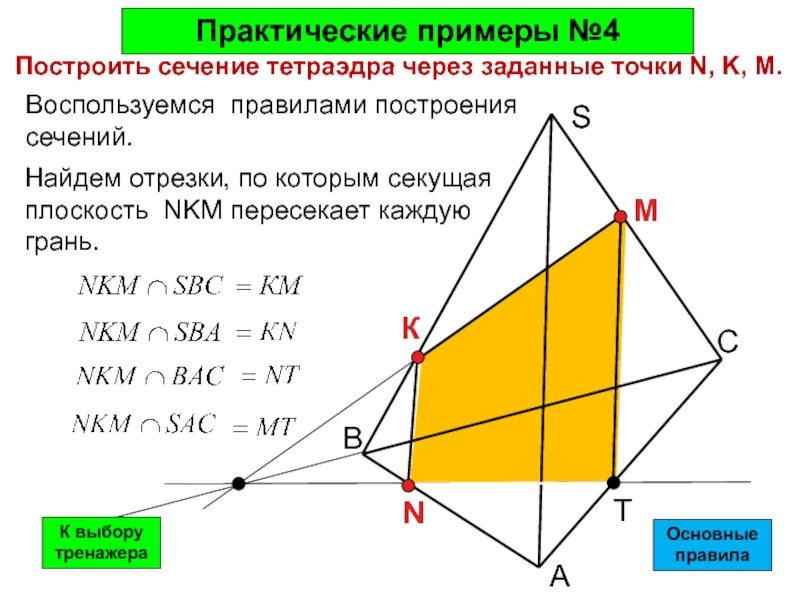
Воспользуемся правилами построения сечений.
А
С
В
S
К
М
N
Т
Построить сечение тетраэдра через заданные точки N,
Найдем отрезки, по которым секущая плоскость NKM пересекает каждую грань.
Практические примеры №4
Основные
правила
К выбору тренажера
Слайд 35
A
B
C
D
M
N
K
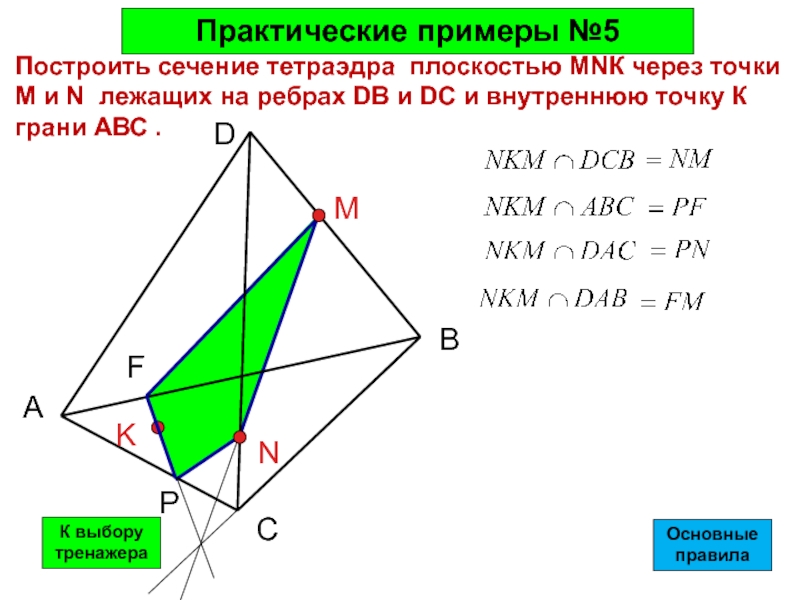
Построить сечение тетраэдра плоскостью МNК через точки М и N лежащих
P
F
Практические примеры №5
Основные
правила
К выбору тренажера
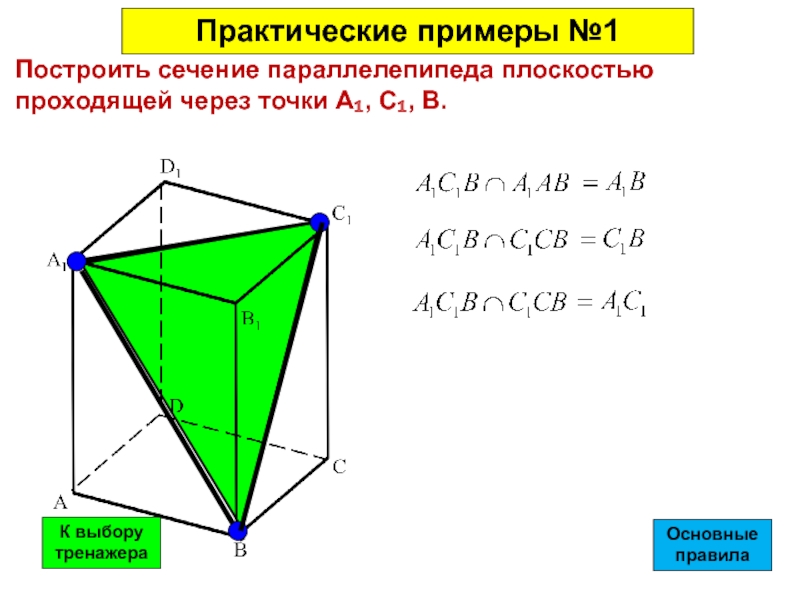
Слайд 36Построить сечение параллелепипеда плоскостью проходящей через точки А₁, С₁, В.
Практические примеры
Основные
правила
К выбору тренажера
Слайд 37
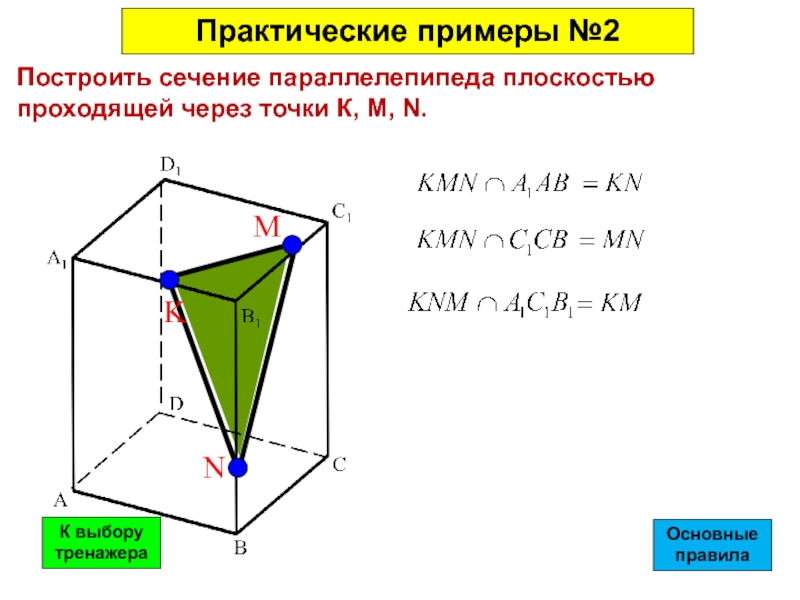
Построить сечение параллелепипеда плоскостью проходящей через точки К, M, N.
K
N
M
Практические примеры
Основные
правила
К выбору тренажера
Слайд 38
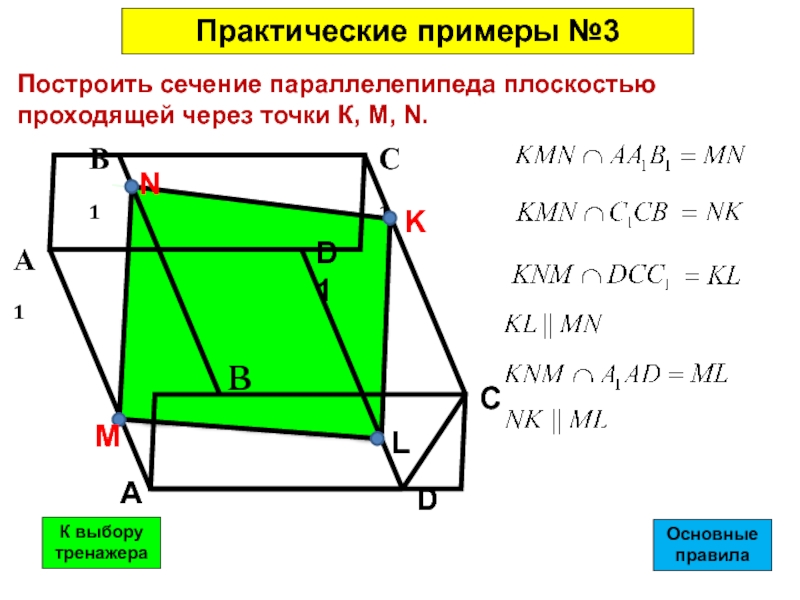
Построить сечение параллелепипеда плоскостью проходящей через точки К, M, N.
Практические примеры
Основные
правила
К выбору тренажера
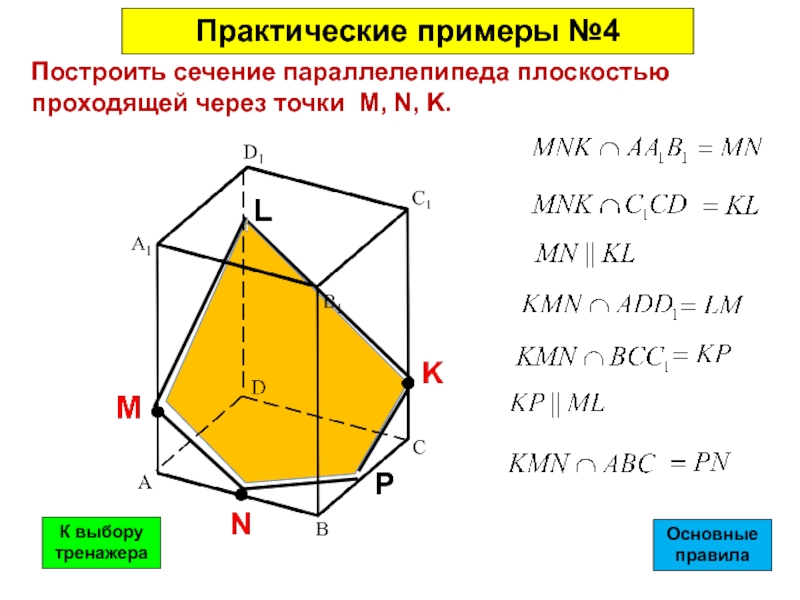
Слайд 39Построить сечение параллелепипеда плоскостью проходящей через точки M, N, K.
L
P
Практические примеры
Основные
правила
К выбору тренажера
Слайд 40
Построить сечение параллелепипеда плоскостью проходящей через точки А, D₁, P.
K
L
Практические примеры
Основные
правила
К выбору тренажера
Слайд 41На гранях куба заданы точки K, L, M. Требуется построить сечение
Т
N
R
Практические примеры №6
Основные
правила
К выбору тренажера
Слайд 42Постройте сечение параллелепипеда проходящее через
точки N, Р, и М.
Практические примеры
Основные
правила
К выбору тренажера
Слайд 43
Постройте сечение параллелепипеда проходящее через
точки N, Р, и М.
Практические примеры
Основные
правила
К выбору тренажера
Слайд 44
Построить сечение параллелепипеда плоскостью проходящей через точки T, P, O.
Практические примеры
Основные
правила
К выбору тренажера
Слайд 45
Построить сечение параллелепипеда плоскостью проходящей через точки K, M, N.
Практические примеры
Основные
правила
К выбору тренажера
Слайд 46
Постройте сечение параллелепипеда проходящее через
точки М, N, и L.
Практические примеры
Основные
правила
К выбору тренажера
Слайд 47Дополнительное задание №1
Постройте сечение параллелепипеда проходящее через
прямую а лежащей
М
N
F
К выбору тренажера
а
Слайд 48
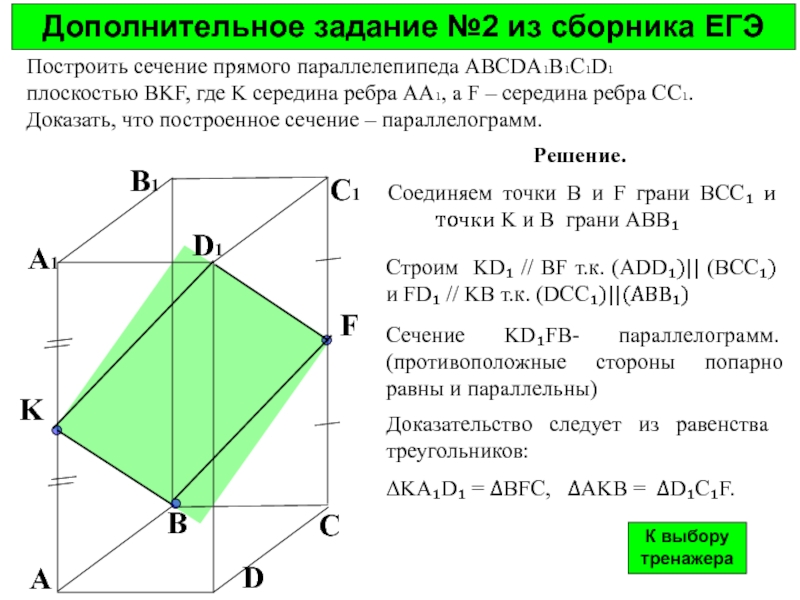
Дополнительное задание №2 из сборника ЕГЭ
К выбору тренажера
Решение.
Соединяем точки B и F грани ВСС₁ и точки K и B грани АВВ₁
A
B
C
D
A1
B1
C1
D1
K
F
Строим KD₁ // BF т.к. (АDD₁)|| (BCC₁) и FD₁ // KB т.к. (DCC₁)||(АВВ₁)
Сечение KD₁FB- параллелограмм. (противоположные стороны попарно равны и параллельны)
Доказательство следует из равенства треугольников:
ΔKA₁D₁ = ΔBFC, ΔAKB = ΔD₁C₁F.
Слайд 49 Домашнее задание
§14, упражнение 79 (б).
Выбери вариант соответствующий твоим ощущениям
К выбору тренажера
До новых встреч
Слайд 50К выбору тренажера
Разминка
гимнастика для глаз
Кабинет, в котором мы занимаемся имеет форму…….
Посмотрите
Слайд 51Литература и интернет ресурсы:
Картинки
1. Учебник. Геометрия: учебник для 10-11 классов средней
2. Поурочные разработки по геометрии дифференцируемый подход В.Я. Яровенко к учебному комплекту Л.С. Атанасян (М.: Просвещение «ВАКО» 2012г.)
Сечения – Маслова О.А.
Сечения – Сейтова Г.Е.
https://yandex.ru/images/search?img_url=http%3A%2F%2Fpresentacid.ru%2Fthumbs%2F0b%2F0bd4683525f1426822e37dbbec4.jpg&p=3&text=%D0%90%D0%BD%D0%B8%D0%BC%D0%B0%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D0%B0%D1%8F%20%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B0%20%D0%BF%D0%BE%20%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%B8&noreask=1&pos=91&rpt=simage&lr=53
https://yandex.ru/images/search?img_url=http%3A%2F%2Fimg-fotki.yandex.ru%2Fget%2F5801%2Fnatgrigvlas.30%2F0_3f968_3dfd17be_S&p=4&text=%D0%90%D0%BD%D0%B8%D0%BC%D0%B0%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D0%B0%D1%8F%20%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B0%20%D0%BF%D0%BE%20%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%B8&noreask=1&pos=128&rpt=simage&lr=53
http://aktinoya.ru/index.php?view=detail&id=3512&option=com_joomgallery&Itemid=64
https://yandex.ru/images/search?img_url=http%3A%2F%2Fliblbt.ru%2Fwp-content%2Fuploads%2F2015%2F07%2F0b32f1a9c4770cc06ea04ed105ec1c6c1-e1328779407289-300x2441-520x245.jpg&text=%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%AD%D0%BA%D0%B7%D1%8E%D0%BF%D0%B5%D1%80%D0%B8&noreask=1&pos=18&lr=53&rpt=simage
https://yandex.ru/images/search?img_url=https%3A%2F%2Fnetoearth.com%2Findex.php%3Fa%3DMfv0Kfa6bO91KgPRoqwSJ2BVMq1BngBFbA9OnO93MqTXKgrCMqiRo29TLq9SKO81bNsQbNiOafl4bsFBIghYnqvOL24TK2PRJ3v1KA4Sn2BA&text=%D0%90%D0%BD%D0%B8%D0%BC%D0%B0%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D1%8B%D0%B5%20%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D1%82%D0%B5%D1%82%D1%80%D0%B0%D1%8D%D0%B4%D1%80%D0%B0%20%D0%B8%20%D0%BF%D0%B0%D1%80%D0%B0%D0%BB%D0%BB%D0%B5%D0%BB%D0%B5%D0%BF%D0%B8%D0%BF%D0%B5%D0%B4%D0%B0&noreask=1&pos=13&lr=53&rpt=simage
https://yandex.ru/images/search?img_url=http%3A%2F%2Fuslide.ru%2Fimages%2F1%2F7738%2F960%2Fimg4.jpg&p=2&text=%D0%90%D0%BD%D0%B8%D0%BC%D0%B0%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D1%8B%D0%B5%20%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D1%82%D0%B5%D1%82%D1%80%D0%B0%D1%8D%D0%B4%D1%80%D0%B0%20%D0%B8%20%D0%BF%D0%B0%D1%80%D0%B0%D0%BB%D0%BB%D0%B5%D0%BB%D0%B5%D0%BF%D0%B8%D0%BF%D0%B5%D0%B4%D0%B0&noreask=1&pos=79&rpt=simage&lr=53
https://yandex.ru/images/search?img_url=http%3A%2F%2Fwww.snappymaths.com%2Fother%2Fshapeandspace%2F3dshapes%2Finteractive%2F3dshapeimm%2Fimages%2Ftripyramid2.jpg&p=8&text=%D0%90%D0%BD%D0%B8%D0%BC%D0%B0%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D1%8B%D0%B5%20%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D1%81%D0%B5%D1%87%D0%B5%D0%BD%D0%B8%D0%B9%20%D1%82%D0%B5%D1%82%D1%80%D0%B0%D1%8D%D0%B4%D1%80%D0%B0%20%D0%B8%20%D0%BF%D0%B0%D1%80%D0%B0%D0%BB%D0%BB%D0%B5%D0%BB%D0%B5%D0%BF%D0%B8%D0%BF%D0%B5%D0%B4%D0%B0&noreask=1&pos=252&rpt=simage&lr=53