- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Аксиомы стереометрии и следствия из них
Содержание
- 1. Аксиомы стереометрии и следствия из них
- 2. Цель урока: ознакомление с понятиями стереометрия, планиметрия,
- 3. Стереометрией называется раздел геометрии, в котором изучаются
- 4. Основными понятия изучающие в планиметрии являются точки,
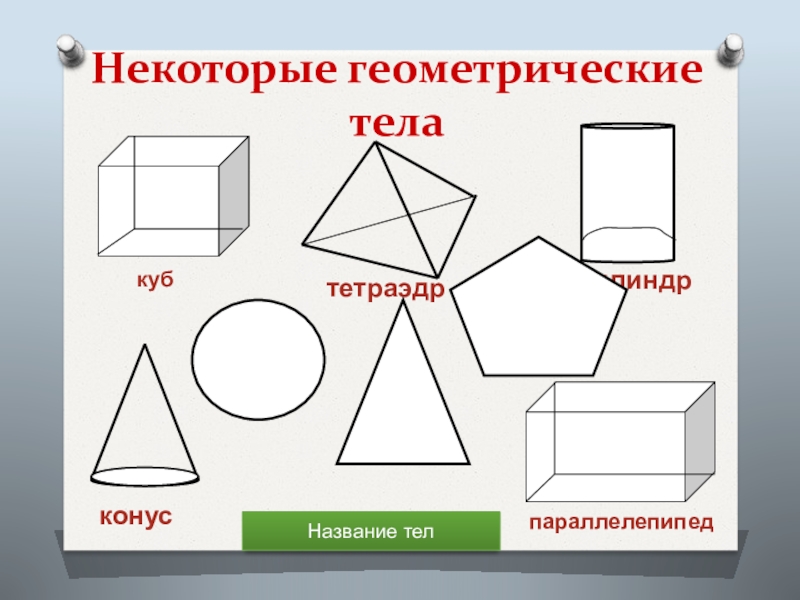
- 5. Некоторые геометрические телакубпараллелепипедтетраэдрцилиндрконусНазвание тел
- 6. Назовите какие геометрические тела вам напоминают предметы,
- 7. Аксиомы – это утверждения, принимаемые без
- 8. Аксиомы стереометрии:А1 : Через любые две различные
- 9. Назовите по рисункуа) плоскости, в которых лежат
- 10. Теорема 1. Через прямую и не
- 11. Теорема 2. Через две пересекающиеся
- 12. АВСα Три данные точки соединены попарно
Слайд 2Цель урока: ознакомление с понятиями стереометрия, планиметрия, аксиомы стереометрии
Задачи урока:
Раскрыть
Развивать умения отличать геометрические тела от геометрических фигур
Воспитывать интерес к математике
Слайд 3Стереометрией называется раздел геометрии, в котором изучаются фигуры, расположенные в пространстве
Основными
Обозначение: A, B, C, D- точки;
α, β, γ - плоскости;
a, b, c, d … - прямые.
Слайд 4Основными понятия изучающие в планиметрии являются точки, прямые, плоскость и расстояние
Планиметрия
Слайд 6Назовите какие геометрические тела вам напоминают предметы, изображенные на этих рисунках:
Назовите предметы из окружающей вас обстановки (в кабинете) напоминающие вам геометрические тела.
Слайд 7 Аксиомы – это утверждения, принимаемые без доказательства
Аксиомы геометрии выражают основные
Слайд 8Аксиомы стереометрии:
А1 : Через любые две различные точки проходит единственная прямая.
А2
А3 : Через любые три точки, не лежащие на одной прямой, проходит плоскость и притом только одна
А4 : Если две различные плоскости имеют общую точку, то они имеют общую прямую.
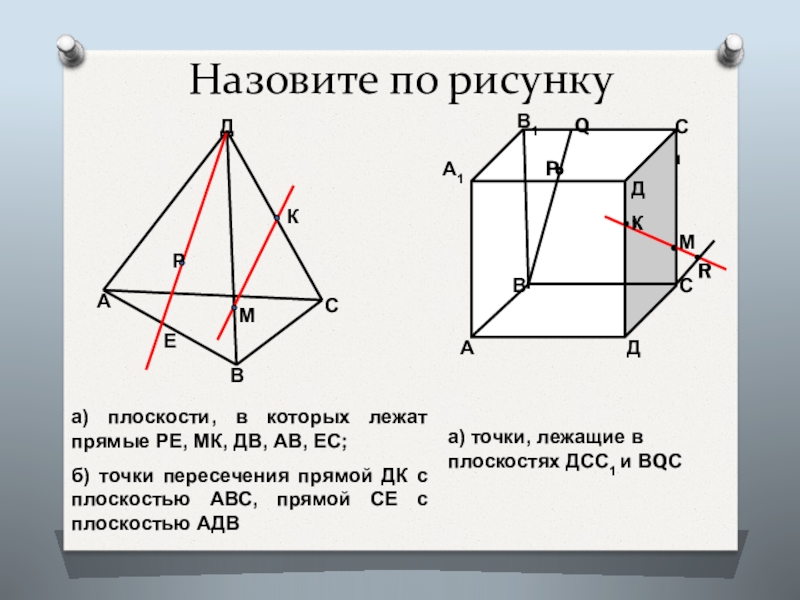
Слайд 9Назовите по рисунку
а) плоскости, в которых лежат прямые РЕ, МК, ДВ,
б) точки пересечения прямой ДК с плоскостью АВС, прямой СЕ с плоскостью АДВ
а) точки, лежащие в плоскостях ДСС1 и ВQС
Слайд 10
Теорема 1. Через прямую и не лежащую на ней точку
Дано:
а, М ¢ а
Доказать:
(а, М) с α
α- единственная
а
М
α
Доказательство :
1. Р, О с а; {Р,О,М} ¢ а
Р
О
По аксиоме А1: через точки Р, О, М проходит плоскость
По аксиоме А2: т.к. две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости, т.е. (а, М) с α
2. Любая плоскость проходящая через прямую а и точку М проходит через точки Р, О, и М, значит по аксиоме А1 она – единственная. Ч.т.д.
Некоторые следствия из аксиом:
Слайд 11
Теорема 2. Через две пересекающиеся прямые проходит плоскость, и
Дано:
а∩b
Доказать:
1. (а∩b) с α
2. α- единственная
а
b
М
Н
α
Доказательство:
1.Через а и Н а, Н b проходит плоскость α.
(М , Н) α, (М,Н) b, значит по А2 все точки b принадлежат плоскости.
2. Плоскость проходит через а и b и она единственная, т.к. любая плоскость, проходящая через прямые а и b, проходит и через Н, значит α – единственная.
Слайд 12
А
В
С
α
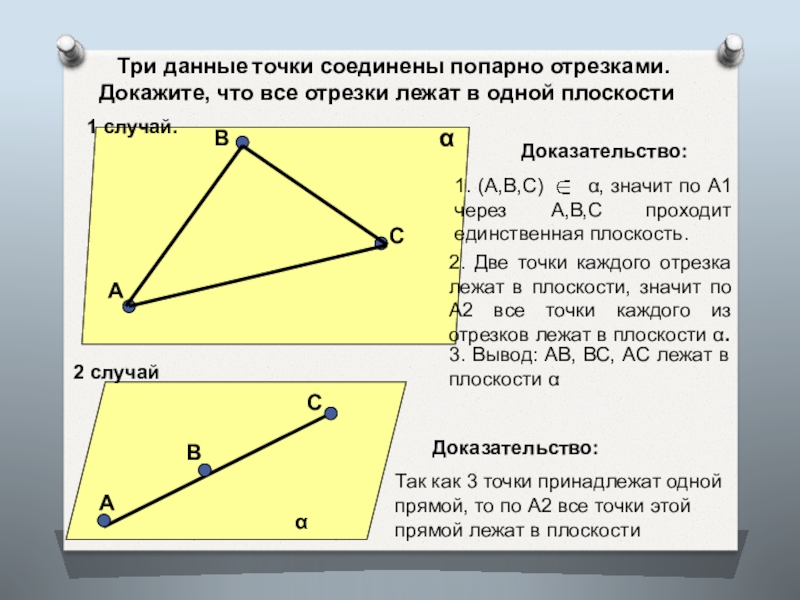
Три данные точки соединены попарно отрезками. Докажите, что все
Доказательство:
1. (А,В,С) α, значит по А1 через А,В,С проходит единственная плоскость.
2. Две точки каждого отрезка лежат в плоскости, значит по А2 все точки каждого из отрезков лежат в плоскости α.
3. Вывод: АВ, ВС, АС лежат в плоскости α
1 случай.
А
В
С
α
2 случай
Доказательство:
Так как 3 точки принадлежат одной прямой, то по А2 все точки этой прямой лежат в плоскости