- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение задач по механике разными способами
Содержание
- 1. Решение задач по механике разными способами
- 2. Лебедева Н.Ю., учитель физики МОУ СОШ №4
- 3. При решении любой задачи рационально выделить четыре
- 4. Тело брошено со скоростью 15м/с
- 5. ЭнергетическийРешение на основе закона сохранения энергииКинематическийРешение на
- 6. Краткая запись условия задачи; СИ.2. Рисунок, направление
- 7. т.к. 10Дано: =
- 8. Алгоритм решения задач на законы сохранения энергииКраткая
- 9. 10Решение Тело брошено со скоростью 15м/с
- 10. Определите тормозной путь троллейбуса, начавшего торможение на
- 11. Определите тормозной путь троллейбуса,
- 12. Алгоритм решения задач на законы Ньютона Краткая
- 13. РешениеОсновное уравнение динамики: Определите тормозной путь
- 14. Определите тормозной путь троллейбуса, начавшего
- 15. Определите скорость тела массой
- 16. Дано: = 1000 т =
- 17. Дано: = 1000 т =
- 18. На невесомом нерастяжимом шнуре, перекинутом
- 19. На невесомом нерастяжимом шнуре, перекинутом
- 20. На невесомом нерастяжимом шнуре, перекинутом
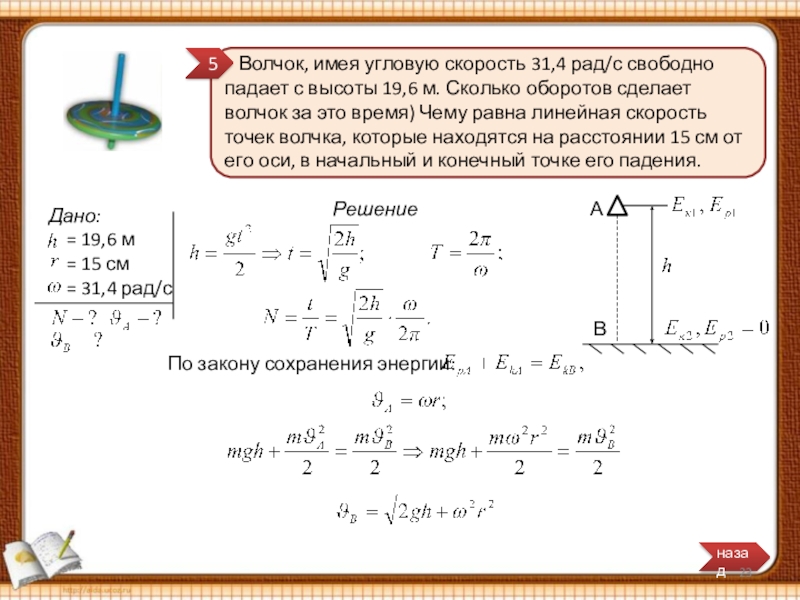
- 21. Волчок, имея угловую скорость 31,4
- 22. Волчок, имея угловую скорость 31,4
- 23. Волчок, имея угловую скорость 31,4
- 24. 1 Проверочная работа Камень падает
- 25. Дано: = 5 мРешение 1 задачи проверочной работыАВРешение кинематическим способомРешение энергетическим способом
- 26. Решение 2 задачи проверочной работыДано: =30Решение
- 27. Слайд 27
- 28. Дано: = 200 кг =
- 29. Дано: = 200 кг =
- 30. Дано: = 200 кг =
- 31. Дано: = 200 кг =
- 32. Решение задаччасти С ЕГЭ
- 33. По гладкой горизонтальной
- 34. По гладкой горизонтальной
- 35. Получили уравнение гармонических колебаний или Из полученной
- 36. По гладкой горизонтальной
- 37. Колебания гармонические, если угол мал
- 38. Подставим уравнения (2) и (3) в уравнение
- 39. Полый металлический шарик
- 40. Если ты умеешь правильно судить себя, значит,
- 41. Решить задачи по выбору: Решить задачи:
- 42. Спасибо за хорошуюработу на уроке
- 43. ЛитератураДряпина А.А. Рефлексия деятельности на уроке. Радуга
Слайд 2Лебедева Н.Ю.,
учитель физики МОУ СОШ №4 им. И.С.Черных г. Томск
Задачи уровня С ЕГЭ, требующие нетрадиционного подхода, решают лишь те учащиеся, которые обладают навыками мыслительной деятельности в совершенстве, представляют задачу в новых условиях, умеют анализировать решение и его результаты…
«Развитие навыков исследовательской деятельности при решении физических задач» Новикова Л. В.
Урок решения задач для учащихся 10 класса естественно-научного профиля
Слайд 3При решении любой задачи рационально выделить четыре этапа:
Анализ текста задачи(заданного
Определение способа (идеи) решения задачи или составление плана решения.
Выполнение запланированных действий (решение в общем виде, проведение опытов и др.), получение ответа в виде числа.
Анализ решения задачи. Подведение итогов.
Слайд 4 Тело брошено со скоростью 15м/с под углом 30 к
0
Анализ условия задачи
Слайд 5Энергетический
Решение на основе закона сохранения энергии
Кинематический
Решение на основе законов кинематики
1
Слайд 6Краткая запись условия задачи; СИ.
2. Рисунок, направление перемещения, скорости, ускорения.
3.
4. Запись уравнение движения тела и уравнений, связывающих кинематические величины.
5. Решение полученной системы уравнений относительно неизвестных.
6. Анализ ответа. Если он противоречит физическому смыслу задачи, то поиск новых идей решения.
1 способ: кинематический
Решение на основе законов кинематики
Алгоритм решения задач на законы кинематики
Слайд 7т.к.
1
0
Дано:
= 15м/с
= 30
0
Решение
Из
Тело брошено со скоростью 15м/с под углом 30 к горизонту. Пренебрегая сопротивлением воздуха, определите, на какую высоту h поднимется данное тело?
Слайд 8Алгоритм решения задач на законы сохранения энергии
Краткая запись условия задачи; СИ.
Чертеж,
Запись закона сохранения или изменения энергии и других необходимых уравнений.
Решение уравнения в общем виде.
Проверка по размерности, выполнение расчетов, оценка достоверность результата, запись ответа.
2 способ: энергетический
Решение на основе закона сохранения энергии
Слайд 91
0
Решение
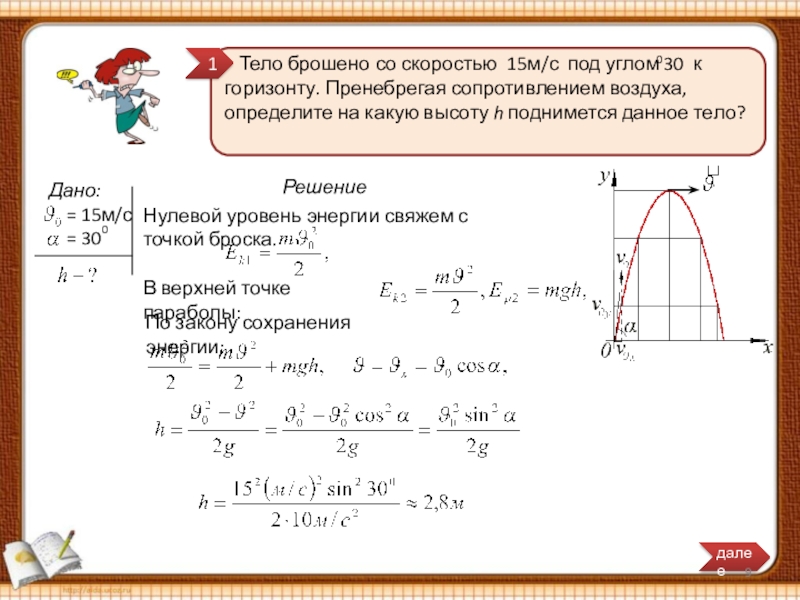
Тело брошено со скоростью 15м/с под углом 30 к
Дано:
= 15м/с
= 30
0
Нулевой уровень энергии свяжем с точкой броска.
В верхней точке параболы:
По закону сохранения энергии:
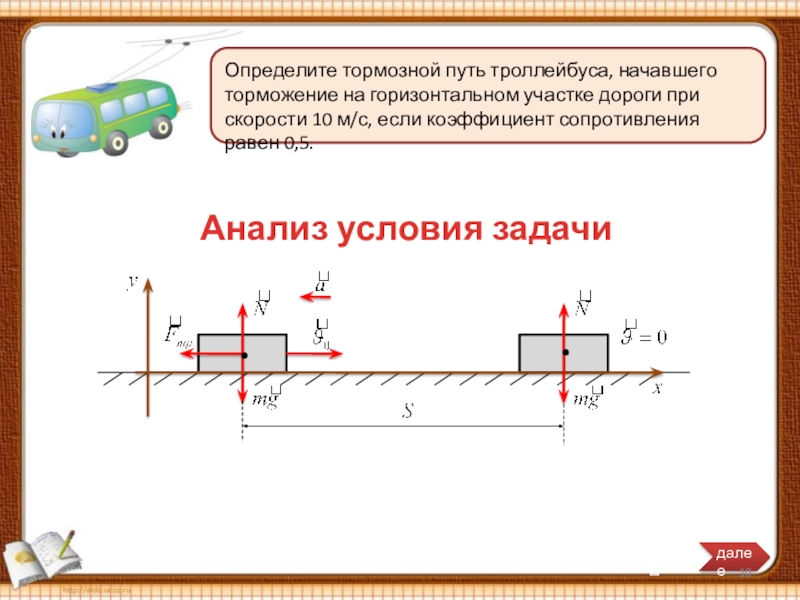
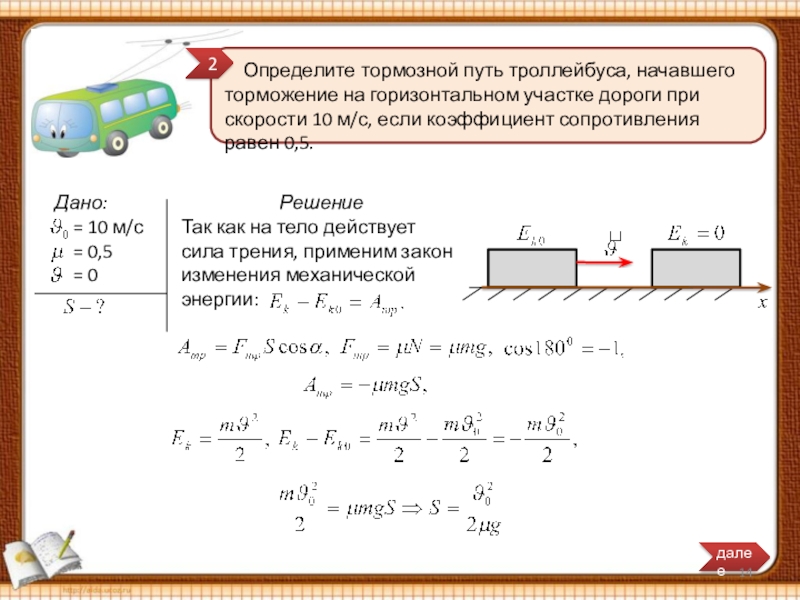
Слайд 10Определите тормозной путь троллейбуса, начавшего торможение на горизонтальном участке дороги при
Энергетический
Динамический
Решение на основе законов Ньютона
Анализ условия задачи
назад
Слайд 11 Определите тормозной путь троллейбуса, начавшего торможение на горизонтальном
Энергетический
Решение на основе закона сохранения энергии
Динамический
Решение на основе законов Ньютона
2
Слайд 12Алгоритм решения задач на законы Ньютона
Краткая запись условия; СИ.
Чертеж.
Выбор системы координат.
Запись второго закона Ньютона в векторном виде.
Запись второго закона Ньютона в проекциях на оси X и Y.
Решение системы уравнений.
Проверка по размерности, расчет числового ответа к задаче и сравнение его с реальными значениями величин.
1 способ: динамический
Решение на основе законов Ньютона
Слайд 13Решение
Основное уравнение динамики:
Определите тормозной путь троллейбуса, начавшего торможение на
В проекциях на оси координат:
2
Слайд 14 Определите тормозной путь троллейбуса, начавшего торможение на горизонтальном участке
Решение
Так как на тело действует сила трения, применим закон изменения механической энергии:
2
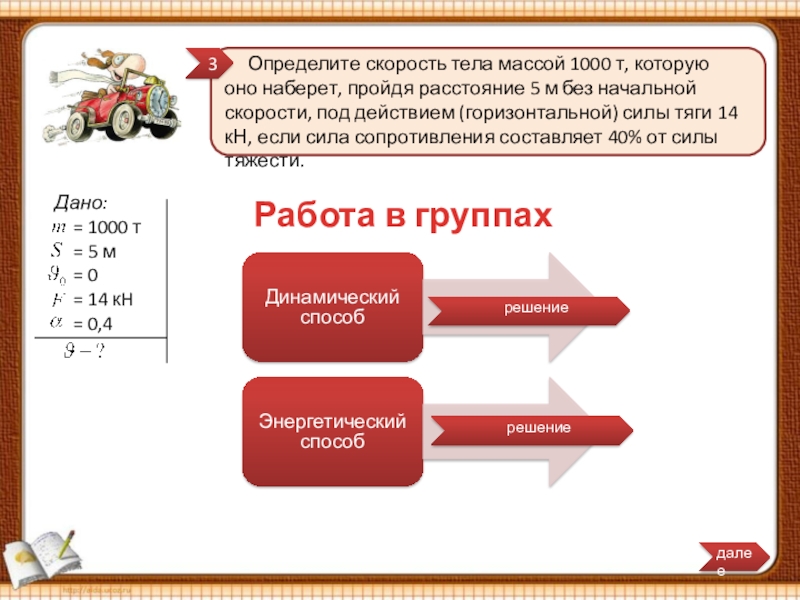
Слайд 15 Определите скорость тела массой 1000 т, которую оно
3
Работа в группах
Слайд 16Дано:
= 1000 т
= 5 м
=
= 14 кH
= 0,4
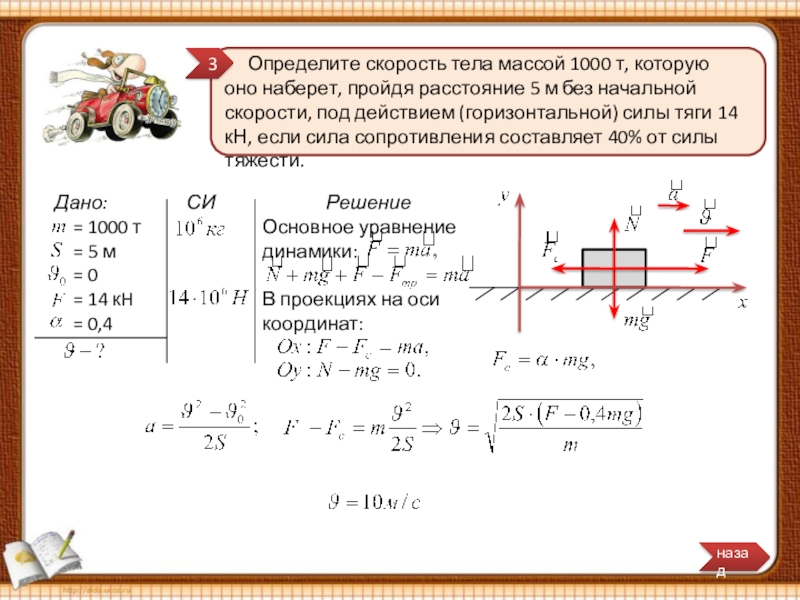
Определите скорость тела массой 1000 т, которую оно наберет, пройдя расстояние 5 м без начальной скорости, под действием (горизонтальной) силы тяги 14 кН, если сила сопротивления составляет 40% от силы тяжести.
СИ
Решение
Основное уравнение динамики:
В проекциях на оси координат:
3
Слайд 17Дано:
= 1000 т
= 5 м
=
= 14 кH
= 0,4
Определите скорость тела массой 1000 т, которую оно наберет, пройдя расстояние 5 м без начальной скорости, под действием (горизонтальной) силы тяги 14 кН, если сила сопротивления составляет 40% от силы тяжести.
СИ
Решение
Так как на тело действует сила трения, применим закон изменения механической энергии:
3
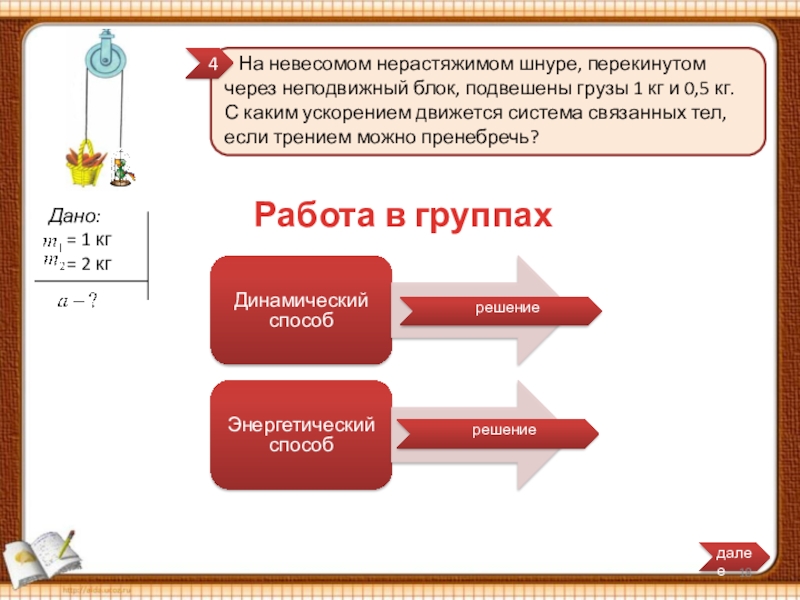
Слайд 18 На невесомом нерастяжимом шнуре, перекинутом через неподвижный блок, подвешены
Дано:
= 1 кг
= 2 кг
4
Работа в группах
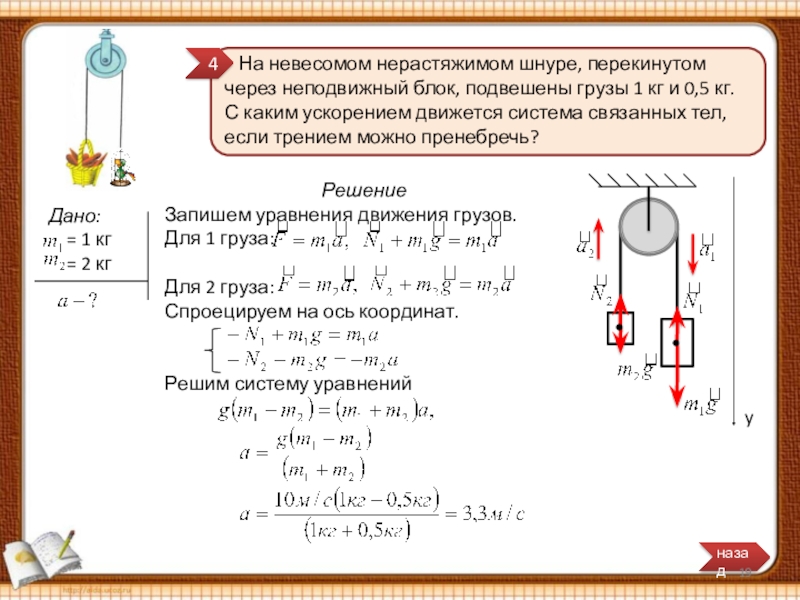
Слайд 19 На невесомом нерастяжимом шнуре, перекинутом через неподвижный блок, подвешены
Дано:
= 1 кг
= 2 кг
Решение
Запишем уравнения движения грузов.
Для 1 груза:
Для 2 груза:
Спроецируем на ось координат.
Решим систему уравнений
y
4
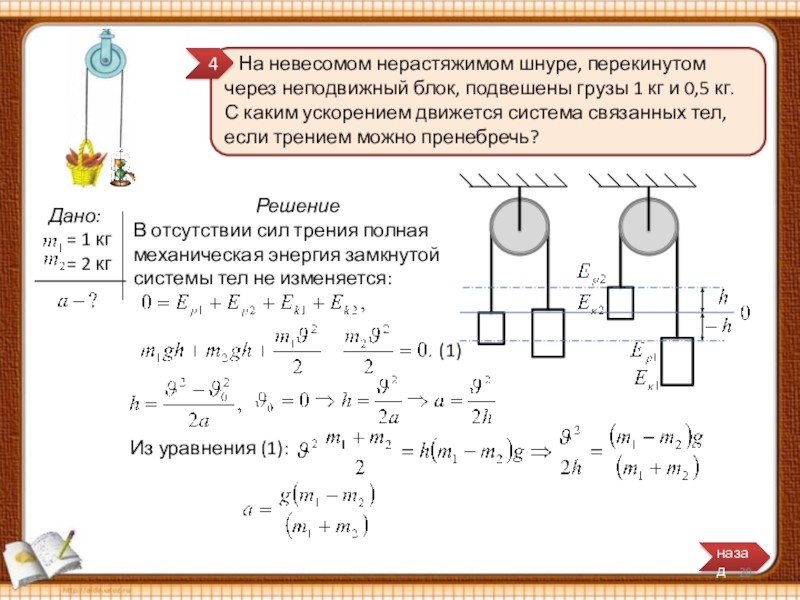
Слайд 20 На невесомом нерастяжимом шнуре, перекинутом через неподвижный блок, подвешены
Дано:
= 1 кг
= 2 кг
Решение
В отсутствии сил трения полная механическая энергия замкнутой системы тел не изменяется:
(1)
Из уравнения (1):
4
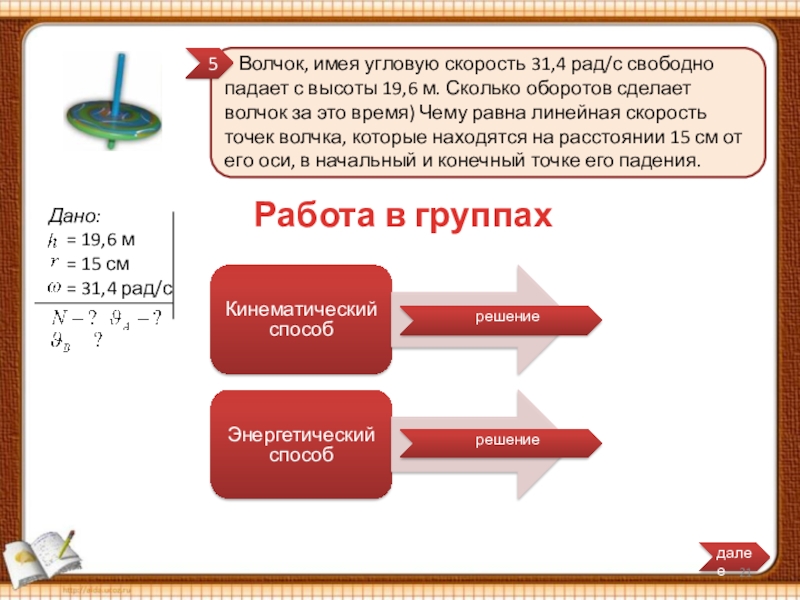
Слайд 21 Волчок, имея угловую скорость 31,4 рад/с свободно падает с
Дано:
= 19,6 м
= 15 см
= 31,4 рад/с
5
Работа в группах
Слайд 22 Волчок, имея угловую скорость 31,4 рад/с свободно падает с
Дано:
= 19,6 м
= 15 см
= 31,4 рад/с
Решение
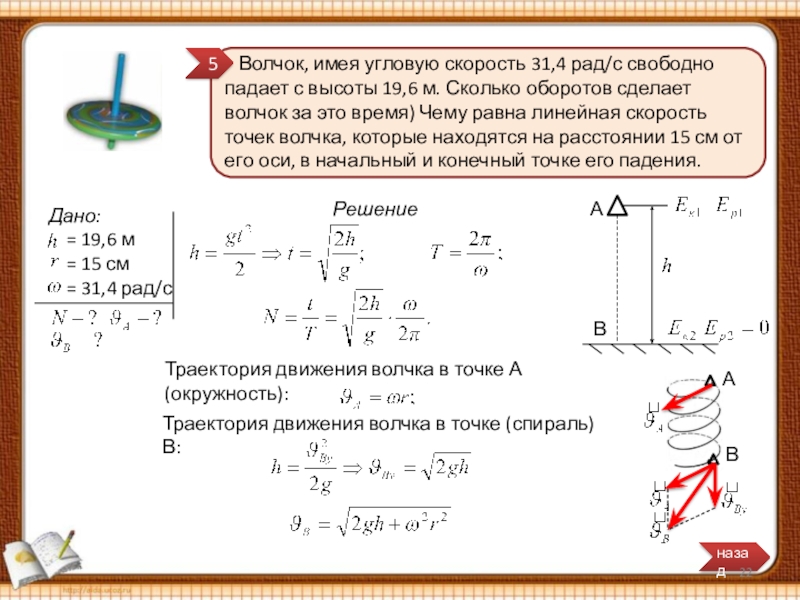
А
Траектория движения волчка в точке А (окружность):
В
Траектория движения волчка в точке (спираль) В:
А
В
5
Слайд 23 Волчок, имея угловую скорость 31,4 рад/с свободно падает с
Дано:
= 19,6 м
= 15 см
= 31,4 рад/с
Решение
А
По закону сохранения энергии:
В
5
Слайд 241
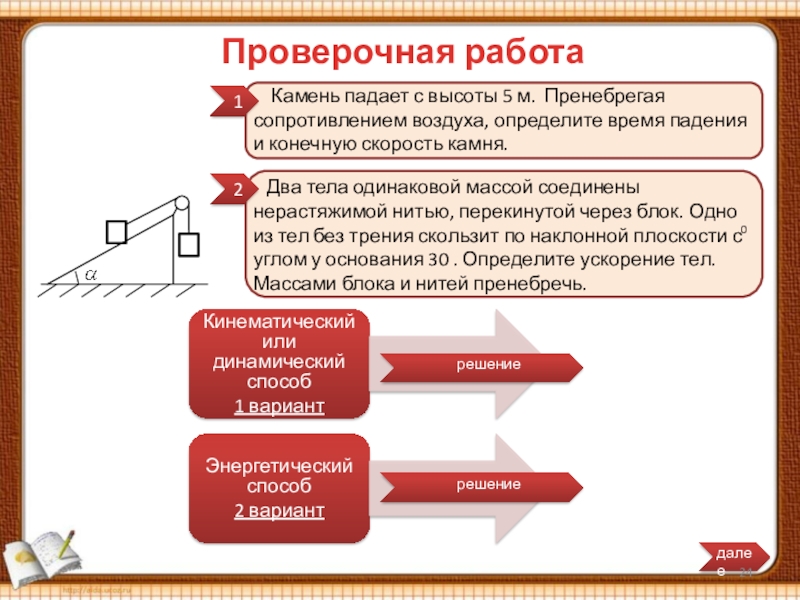
Проверочная работа
Камень падает с высоты 5 м.
Два тела одинаковой массой соединены нерастяжимой нитью, перекинутой через блок. Одно из тел без трения скользит по наклонной плоскости с углом у основания 30 . Определите ускорение тел. Массами блока и нитей пренебречь.
2
0
Слайд 25Дано:
= 5 м
Решение 1 задачи проверочной работы
А
В
Решение кинематическим способом
Решение
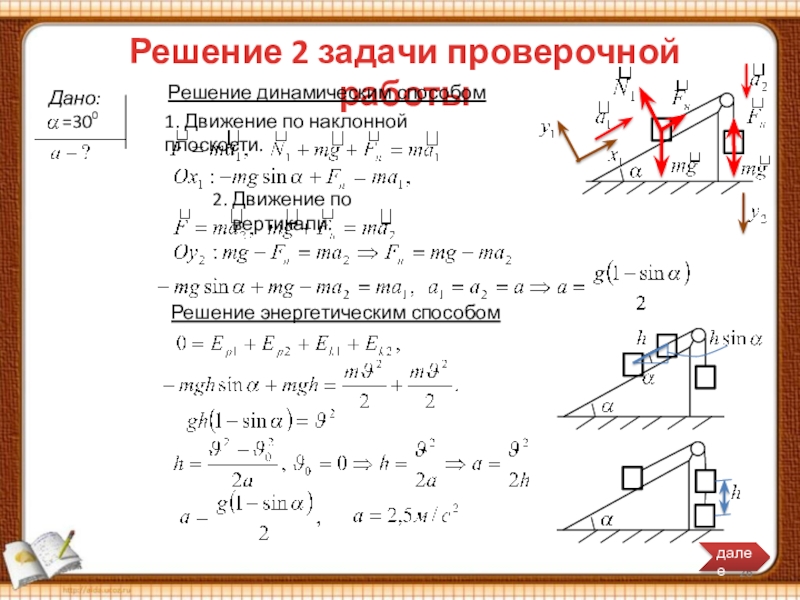
Слайд 26Решение 2 задачи проверочной работы
Дано:
=30
Решение динамическим способом
1. Движение по
2. Движение по вертикали.
Решение энергетическим способом
0
Слайд 28Дано:
= 200 кг
= 60 м
=
= 0,14
= 0,4
Санки с грузом 200 кг скатываются с горки под углом 14 к горизонту. Длина спуска 60 м, коэффициент трения скольжения саней 0,14. Определите, на какое расстояние по горизонтали прокатятся санки после спуска до полной остановки. Считать , что на переходе от наклонной плоскости к горизонтали трение отсутствует.)
6
Слайд 29Дано:
= 200 кг
= 60 м
=
= 0,14
= 0,4
Санки с грузом 200 кг скатываются с горки под углом 14 к горизонту. Длина спуска 60 м, коэффициент трения скольжения саней 0,14. Определите, на какое расстояние по горизонтали прокатятся санки после спуска до полной остановки. Считать , что на переходе от наклонной плоскости к горизонтали трение отсутствует.)
Решение
1. Движение по наклонной плоскости.
6
Слайд 30Дано:
= 200 кг
= 60 м
=
= 0,14
= 30
Санки с грузом 200 кг скатываются с горки под углом 14 к горизонту. Длина спуска 60 м, коэффициент трения скольжения саней 0,14. Определите, на какое расстояние по горизонтали прокатятся санки после спуска до полной остановки. Считать , что на переходе от наклонной плоскости к горизонтали трение отсутствует.)
Решение
2. Движение по горизонтали.
Так как
0
6
Слайд 31Дано:
= 200 кг
= 60 м
=
= 0,14
= 0,4
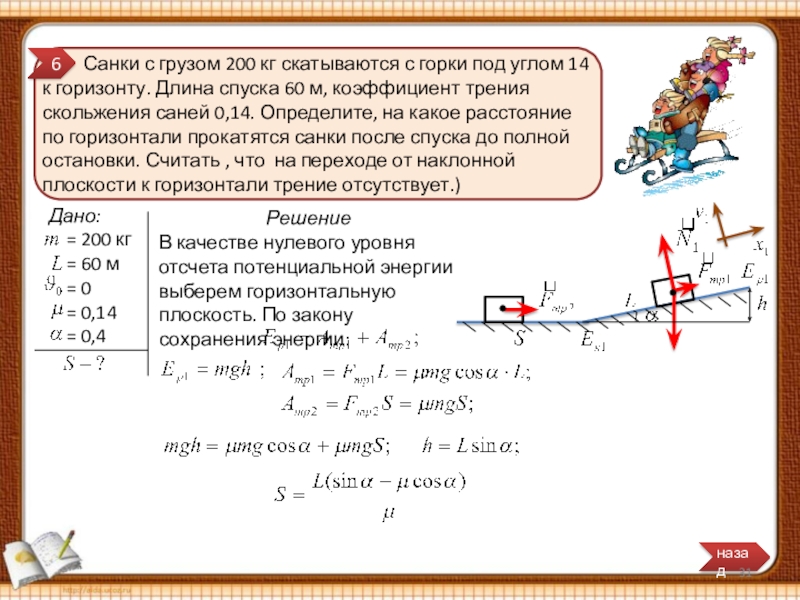
Санки с грузом 200 кг скатываются с горки под углом 14 к горизонту. Длина спуска 60 м, коэффициент трения скольжения саней 0,14. Определите, на какое расстояние по горизонтали прокатятся санки после спуска до полной остановки. Считать , что на переходе от наклонной плоскости к горизонтали трение отсутствует.)
Решение
В качестве нулевого уровня отсчета потенциальной энергии выберем горизонтальную плоскость. По закону сохранения энергии:
6
Слайд 33 По гладкой горизонтальной направляющей длины 2L скользит
Во сколько раз следует уменьшить заряд бусинки, чтобы период ее колебаний увеличился в 3 раза?
Дано:
Анализ решения задачи
1. Сместим бусинку на малое расстояние от положения равновесия.
2. На бусинку действуют кулоновские силы со стороны зарядов +q.
4. Бусинка начинает совершать гармонические колебания.
3. Так как , появилось ускорение, но оно переменное.
5. Период колебаний можно выразить через :
7
6. Частоту можно найти из уравнения ускорения или скорости тела.
7. Выразив частоту, найдем искомую величину.
Слайд 34 По гладкой горизонтальной направляющей длины 2L скользит
Во сколько раз следует уменьшить заряд бусинки, чтобы период ее колебаний увеличился в 3 раза?
Дано:
Решение
Динамический способ
7
Слайд 35Получили уравнение гармонических колебаний
или
Из полученной формулы видно, чтобы период
Рассмотрим знаменатель. По условию
Рассмотрим числитель.
Слайд 36 По гладкой горизонтальной направляющей длины 2L скользит
Во сколько раз следует уменьшить заряд бусинки, чтобы период ее колебаний увеличился в 3 раза?
Дано:
Решение
Энергетический способ
7
Слайд 37Колебания гармонические, если угол мал
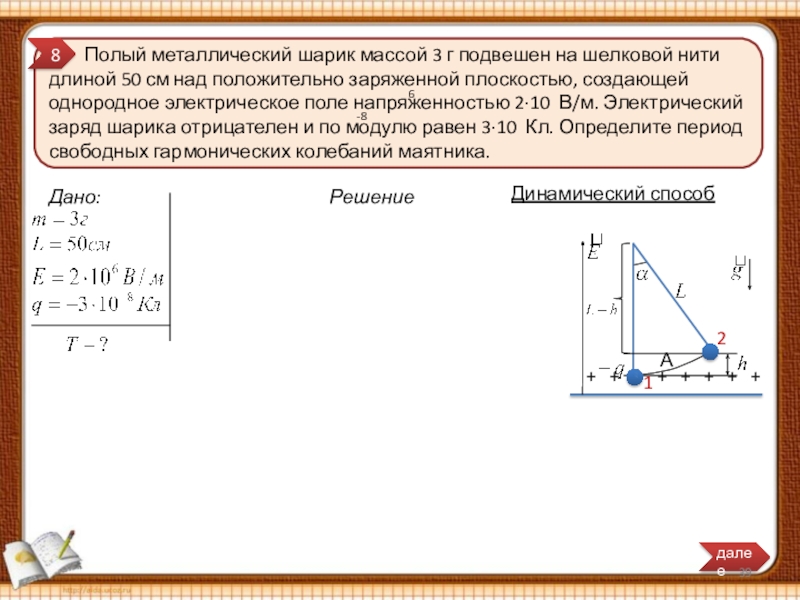
Полый металлический шарик массой 3 г подвешен на шелковой нити длиной 50 см над положительно заряженной плоскостью, создающей однородное электрическое поле напряженностью 2∙10 В/м. Электрический заряд шарика отрицателен и по модулю равен 3∙10 Кл. Определите период свободных гармонических колебаний маятника.
Дано:
Решение
+ + + + + + + +
А
1
2
В состоянии 1:
В состоянии 2:
По закону сохранения энергии:
Так как поле однородно
Из рисунка
-8
6
Энергетический способ
8
Слайд 38Подставим уравнения (2) и (3) в уравнение (1), получим
При
Тогда
Слайд 39 Полый металлический шарик массой 3 г подвешен
Дано:
Решение
+ + + + + + + +
А
1
2
-8
6
Динамический способ
8
Слайд 40Если ты умеешь правильно судить себя, значит, ты поистине мудр.
Антуан де
Рефлексия
Оцени свою работу на уроке по предложенным параметрам по трех бальной системе.
Слайд 41Решить задачи по выбору:
Решить задачи:
1. Кинетическая энергия тела
Домашнее задание
Повторить:
Алгоритм решения задач кинематическим способом
Алгоритм решения задач динамическим способом
Алгоритм решения задач энергетическим способом
Составить задачу, которую можно решить различными способами.
Слайд 43Литература
Дряпина А.А. Рефлексия деятельности на уроке. Радуга успеха. Сайт кафедры развития
Мякишев Г.Я., Буховцев Б.Б. Физика: Учебник для 10 класса ООУ. - М.: Просвещение, 2009.
Орлов В.Ф. Практика решения физических задач: 10-11 классы: учебное пособие для учащихся общеобразовательных учреждений/ В.А. Орлов, Ю.А. Сауров. – М.: Вентана-Граф, 2010.
Парфентьева Н.А. Сборник задач по физике: базовый и профил. Уровни: для 10-11 кл. общеобразоват. Учреждений/ Н.А. Парфентьева. – М.: Просвещение, 2007.
Фоминых О.Ю. Решение задач механики динамическим и энергетическим способами.- Газета «Физика» №2/99
Шабалин Е.И. Репетитор по физике. Задачи ЕГЭ. http://www.reppofiz.info/ege.html